数据结构与算法之美-11 图 深度和广度优先搜索

本文地址

---

目录

目录

• 目录
• 30 | 图的表示：如何存储微博、微信等社交网络中的好友关系？
  • 图的概念
    • 微信：无向图
    • 微博：有向图
    • QQ：带权图
  • 如何存储图
    • 邻接矩阵 Adjacency Matrix
    • 邻接表 Adjacency List
  • 如何存储微博的好友关系
• 31 | 深度和广度优先搜索：如何找出社交网络中的三度好友关系？
  • 什么是搜索算法
  • 无向图的代码
  • 广度优先搜索 BFS
    • 代码实现
    • 分解示意图
    • 复杂度分析
  • 深度优先搜索 DFS
    • 案例：走迷宫
    • 代码实现
    • 复杂度分析
  • 如何找出社交网络中用户的三度好友关系
  • 内容小结

30 | 图的表示：如何存储微博、微信等社交网络中的好友关系？

图的概念

和树比起来，图（Graph）是一种更加复杂的非线性表结构。

树中的元素叫做节点，图中的元素叫做顶点（vertex），图中的一个顶点可以与任意其他顶点建立连接关系，这种建立的关系叫做边（edge）。

微信：无向图

我们可以把每个用户看作一个顶点。如果两个用户之间互加好友，那就在两者之间建立一条边。所以，整个微信的好友关系就可以用一张图来表示。其中，每个用户有多少个好友，对应到图中，就叫做顶点的度（degree），就是跟顶点相连接的边的条数。

微博：有向图

微博的社交关系跟微信相比更加复杂一点。微博允许单向关注，也就是说，用户 A 关注了用户 B，但用户 B 可以不关注用户 A。

我们可以把刚刚讲的图结构稍微改造一下，引入边的“方向”的概念。

如果用户 A 关注了用户 B，我们就在图中画一条从 A 到 B 的带箭头的边，来表示边的方向。如果用户 A 和用户 B 互相关注了，那我们就画一条从 A 指向 B 的边，再画一条从 B 指向 A 的边。我们把这种边有方向的图叫做有向图。以此类推，我们把边没有方向的图就叫做无向图。

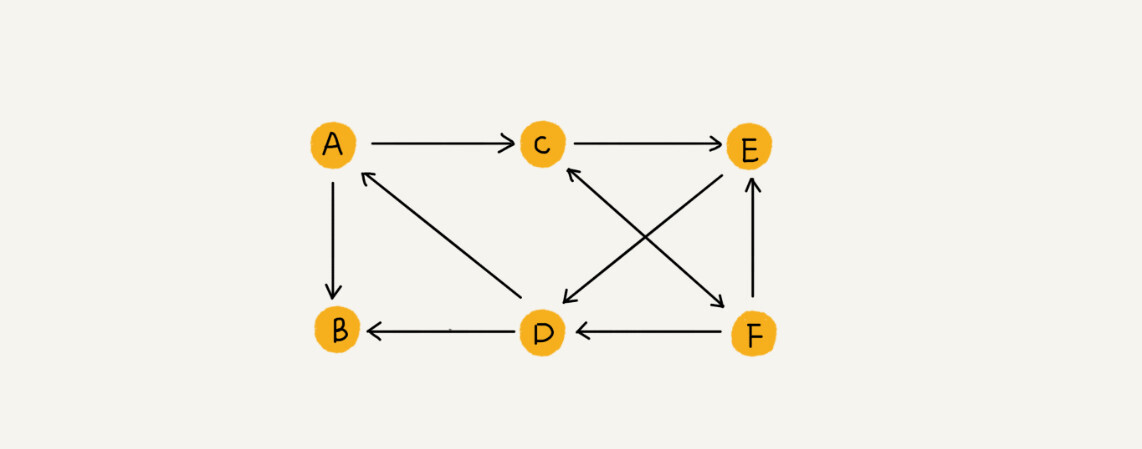
无向图中有“度”这个概念，表示一个顶点有多少条边。在有向图中，我们把度分为入度（In-degree）和出度（Out-degree）。

顶点的入度，表示有多少条边指向这个顶点；顶点的出度，表示有多少条边是以这个顶点为起点指向其他顶点。对应到微博的例子，入度就表示有多少粉丝，出度就表示关注了多少人。

QQ：带权图

QQ 中的社交关系要更复杂一点。QQ 不仅记录了用户之间的好友关系，还记录了两个用户之间的亲密度，如果两个用户经常往来，那亲密度就比较高；如果不经常往来，亲密度就比较低。如何在图中记录这种好友关系的亲密度呢？

这里就要用到另一种图，带权图（weighted graph）。在带权图中，每条边都有一个权重（weight），我们可以通过这个权重来表示 QQ 好友间的亲密度。

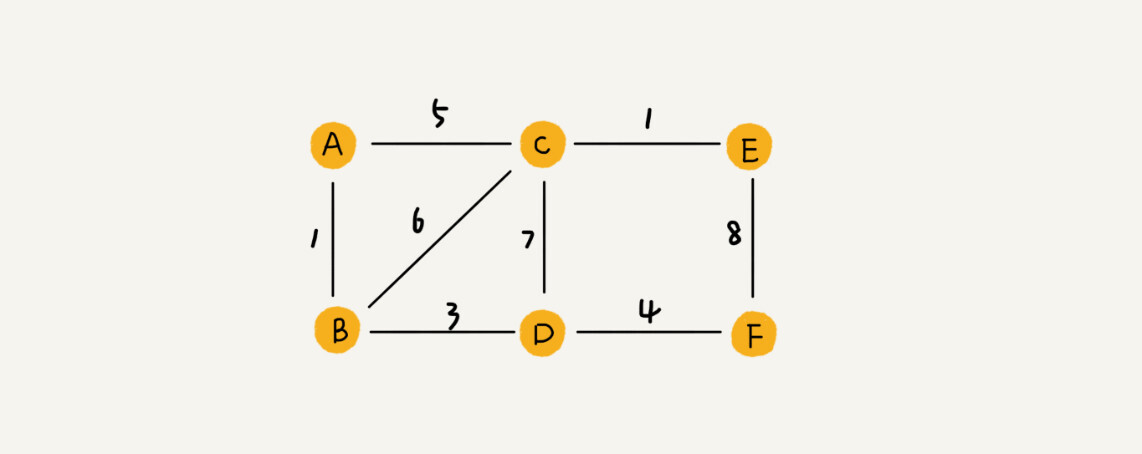
如何存储图

掌握了图的概念之后，我们再来看下，如何在内存中存储图这种数据结构呢？

邻接矩阵 Adjacency Matrix

图最直观的一种存储方法就是，邻接矩阵（Adjacency Matrix）。

邻接矩阵的底层依赖一个二维数组

• 对于无向图来说，如果顶点 i 与顶点 j 之间有边，我们就将 A[i][j] 和 A[j][i] 标记为 1
• 对于有向图来说，如果顶点 i 到顶点 j 之间，有一条箭头从顶点 i 指向顶点 j 的边，那我们就将 A[i][j] 标记为 1；同理，如果有一条箭头从顶点 j 指向顶点 i 的边，我们就将 A[j][i] 标记为 1
• 对于带权图，数组中就存储相应的权重

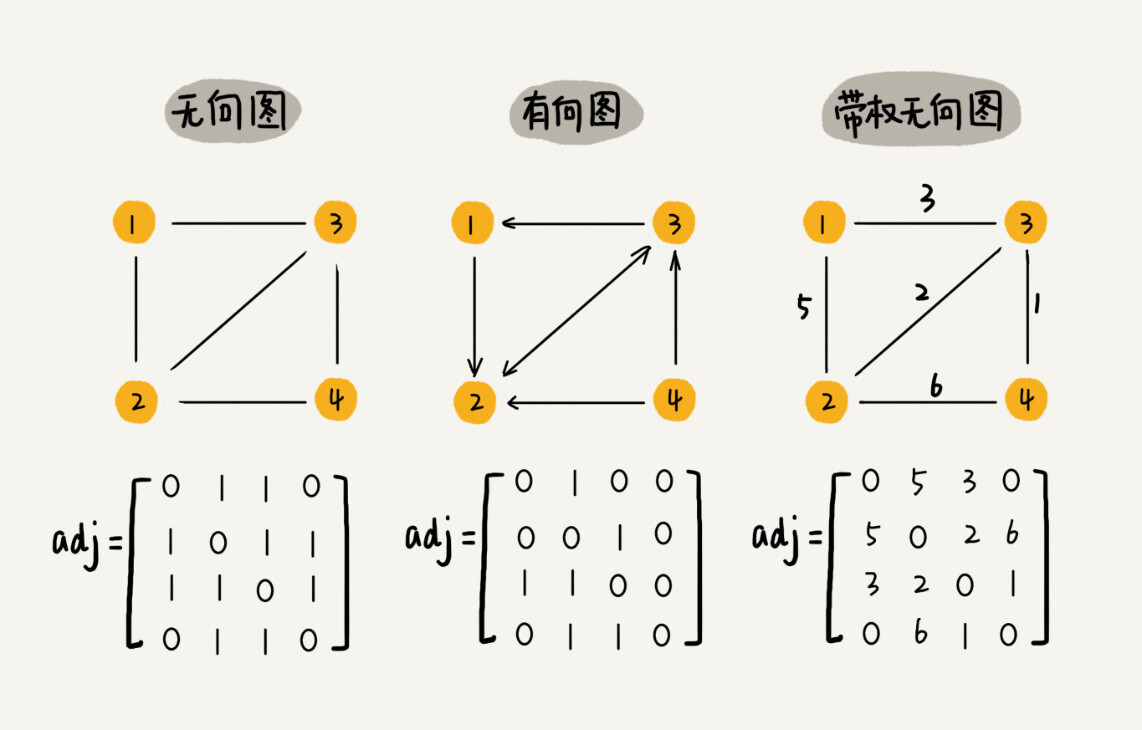
用邻接矩阵存储图有很多优点：

• 首先，邻接矩阵的存储方式简单、直接，因为基于数组，所以在获取两个顶点的关系时非常高效。
• 其次，用邻接矩阵存储图方便计算，因为可以将很多图的运算转换成矩阵之间的运算。比如求解最短路径问题时会提到一个 Floyd-Warshall 算法，就是利用矩阵循环相乘若干次得到结果。

但是缺点是比较浪费存储空间

• 首先，对于无向图来说，如果 A[i][j] 等于 1，那 A[j][i] 也肯定等于 1。实际上，我们只需要存储一个就可以了。也就是说，无向图的二维数组中，如果我们将其用对角线划分为上下两部分，那我们只需要利用上面或者下面这样一半的空间就足够了，另外一半白白浪费掉了。
• 其次，如果我们存储的是稀疏图（Sparse Matrix），也就是说，顶点很多，但每个顶点的边并不多，那邻接矩阵的存储方法就更加浪费空间了。比如微信有好几亿的用户，对应到图上就是好几亿的顶点。但是每个用户的好友并不会很多，一般也就三五百个而已。如果我们用邻接矩阵来存储，那绝大部分的存储空间都被浪费了。

邻接表 Adjacency List

针对上面邻接矩阵比较浪费内存空间的问题，我们来看另外一种图的存储方法，邻接表（Adjacency List）。

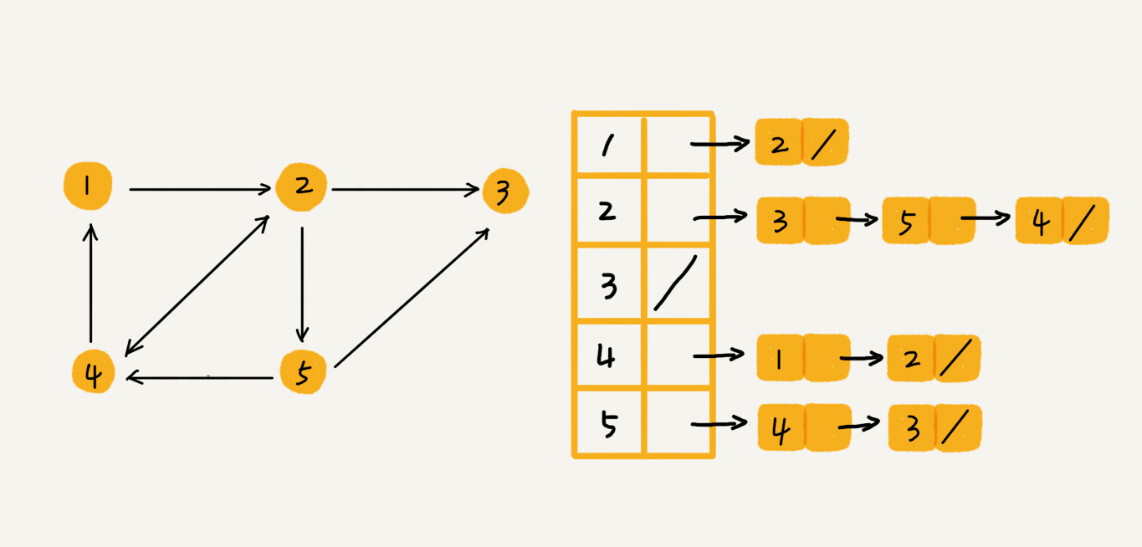
乍一看，邻接表有点像散列表，每个顶点对应一条链表，链表中存储的是与这个顶点相连接的其他顶点。

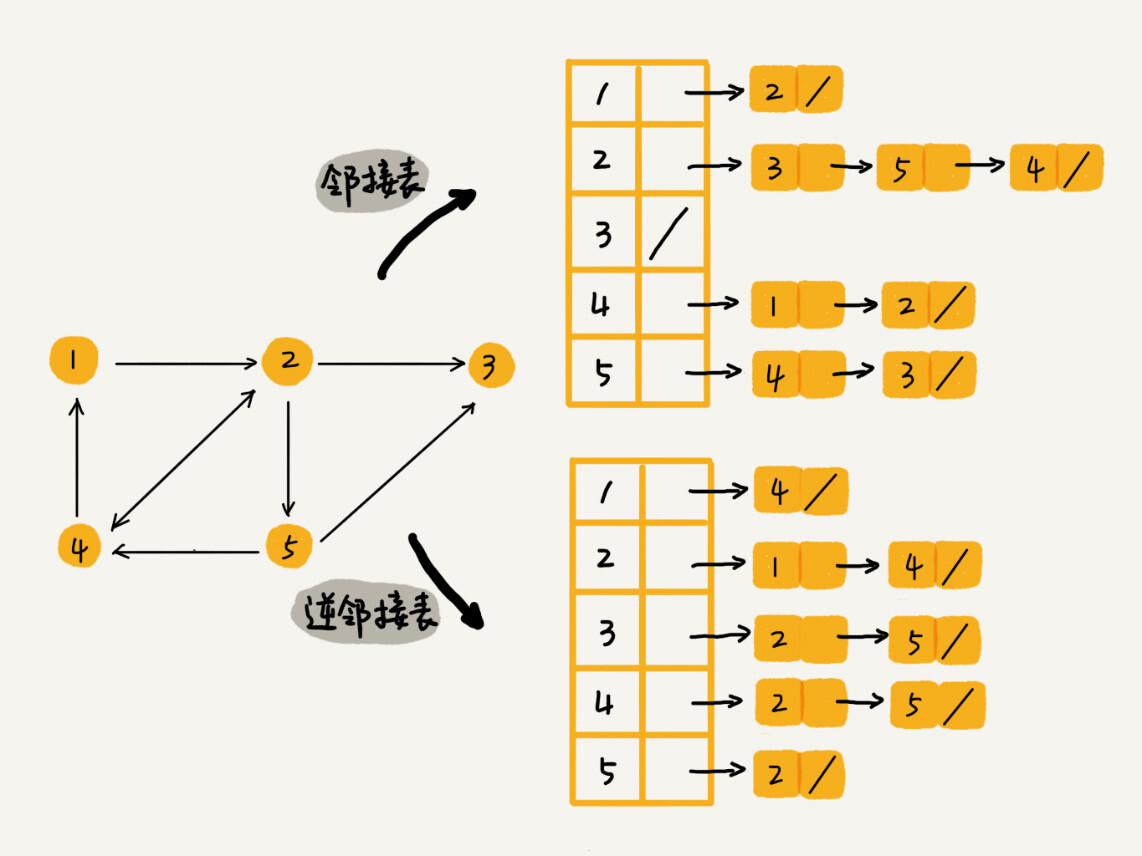
上图中画的是一个有向图的邻接表存储方式，每个顶点对应的链表里面，存储的是指向的顶点。对于无向图来说，也是类似的，不过，每个顶点的链表中存储的是，跟这个顶点有边相连的顶点。

邻接矩阵存储起来比较浪费空间，但是使用起来比较节省时间。相反，邻接表存储起来比较节省空间，但是使用起来就比较耗时间。

• 就像图中的例子，如果我们要确定是否存在一条从顶点 2 到顶点 4 的边，那我们就要遍历顶点 2 对应的那条链表，看链表中是否存在顶点 4。
• 而且，链表的存储空间不连续，无法利用局部性原理，将前后的节点都cache住。
• 所以，比起邻接矩阵的存储方式，在邻接表中查询两个顶点之间的关系就没那么高效了。

邻接表长得很像散列，我们也可以将邻接表同散列表一样，将邻接表中的链表改成平衡二叉查找树(比如红黑树)，这样，我们就可以更加快速地查找两个顶点之间是否存在边了。

如何存储微博的好友关系

数据结构是为算法服务的，所以具体选择哪种存储方法，与期望支持的操作有关系。针对微博用户关系，假设我们需要支持下面这样几个操作：

• 判断用户 A 是否关注了用户 B
• 判断用户 A 是否是用户 B 的粉丝
• 用户 A 关注用户 B
• 用户 A 取消关注用户 B
• 根据用户名称的首字母排序，分页获取用户的粉丝列表
• 根据用户名称的首字母排序，分页获取用户的关注列表

关于如何存储一个图，前面我们讲到两种主要的存储方法，邻接矩阵和邻接表。因为社交网络是一张稀疏图，使用邻接矩阵存储比较浪费存储空间。所以，这里我们采用邻接表来存储。

不过，用一个邻接表来存储这种有向图是不够的。我们去查找某个用户关注了哪些用户非常容易，但是如果要想知道某个用户都被哪些用户关注了，也就是用户的粉丝列表，是非常困难的。

基于此，我们需要一个逆邻接表。

• 邻接表中存储了用户的关注关系，逆邻接表中存储的是用户的被关注关系。
• 对应到图上，邻接表中，每个顶点的链表中存储的就是这个顶点指向的顶点；逆邻接表中，每个顶点的链表中，存储的是指向这个顶点的顶点。
• 如果要查找某个用户关注了哪些用户，我们可以在邻接表中查找；如果要查找某个用户被哪些用户关注了，我们从逆邻接表中查找。

基础的邻接表不适合快速判断两个用户之间是否存在关注与被关注的关系，所以我们将邻接表中的链表改为支持快速查找的动态数据结构。选择哪种动态数据结构呢，红黑树、跳表、有序动态数组还是散列表？

因为我们需要按照用户名称的首字母排序，分页来获取用户的粉丝列表或者关注列表，用跳表这种结构再合适不过了。这是因为，跳表插入、删除、查找都非常高效，时间复杂度是 O(logn)，空间复杂度上稍高，是 O(n)。最重要的一点，跳表中存储的数据本来就是有序的了，分页获取粉丝列表或关注列表非常高效。

如果对于小规模的数据，比如社交网络中只有几万、几十万个用户，我们可以将整个社交关系存储在内存中，但是如果像微博那样有上亿的用户，数据规模太大，我们就无法全部存储在内存中了。这个时候该怎么办呢？

我们可以通过哈希算法等数据分片方式，将邻接表、逆邻接表存储在不同的机器上。当要查询顶点与顶点关系的时候，我们就利用同样的哈希算法，先定位顶点所在的机器，然后再在相应的机器上查找。

除此之外，我们还有另外一种解决思路，就是利用外部存储（比如数据库），因为外部存储的存储空间要比内存会宽裕很多。

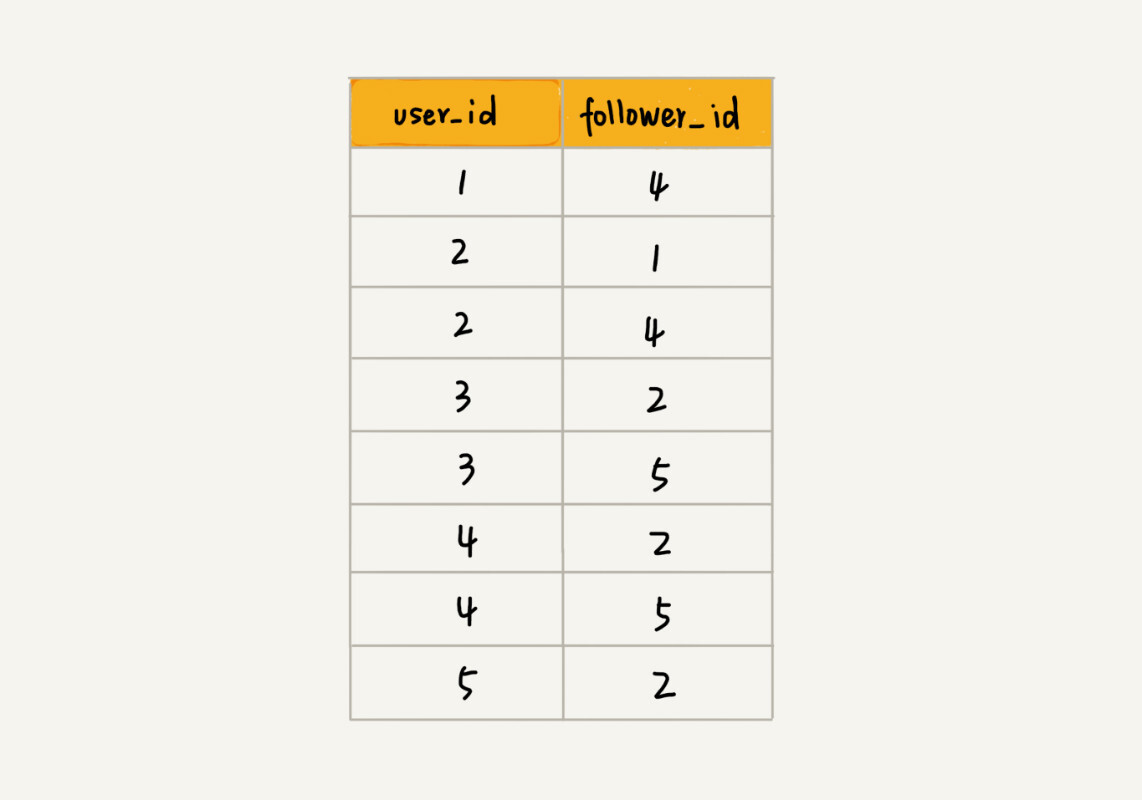
为了高效地支持前面定义的操作，我们可以在数据库表上建立多个索引，比如第一列、第二列，给这两列都建立索引。

31 | 深度和广度优先搜索：如何找出社交网络中的三度好友关系？

在社交网络中，有一个六度分割理论，具体是说，你与世界上的另一个人间隔的关系不会超过六度，也就是说平均只需要六步就可以联系到任何两个互不相识的人。

一个用户的一度连接用户就是他的好友，二度连接用户就是他好友的好友，三度连接用户就是他好友的好友的好友。在社交网络中，我们往往通过用户之间的连接关系，来实现推荐可能认识的人这么一个功能。那么，如何找出一个用户的所有三度好友关系呢？

这就要用到今天要讲的深度优先和广度优先搜索算法。

什么是搜索算法

算法是作用于具体数据结构之上的，而深度优先搜索算法和广度优先搜索算法，都是基于图这种数据结构的。

图上的搜索算法，最直接的理解就是：在图中找出，从一个顶点出发，到另一个顶点的路径。

具体方法有很多，今天要讲的是最简单、最暴力的深度优先、广度优先搜索，除此之外，还有 A*、IDA* 等启发式搜索算法。

无向图的代码

// 无向图
public class Graph {
    private int v; // 顶点的个数
    private LinkedList<Integer> adj[]; // 用邻接表来存储图
    
    public Graph(int v) {
        this.v = v;
        adj = new LinkedList[v];
        for (int i = 0; i < v; ++i) {
            adj[i] = new LinkedList<>();
        }
    }
    
    public void addEdge(int s, int t) {
        adj[s].add(t); // 无向图一条边存两次
        adj[t].add(s);
    }
}

广度优先搜索 BFS

广度优先搜索（Breadth-First-Search），简称 BFS。

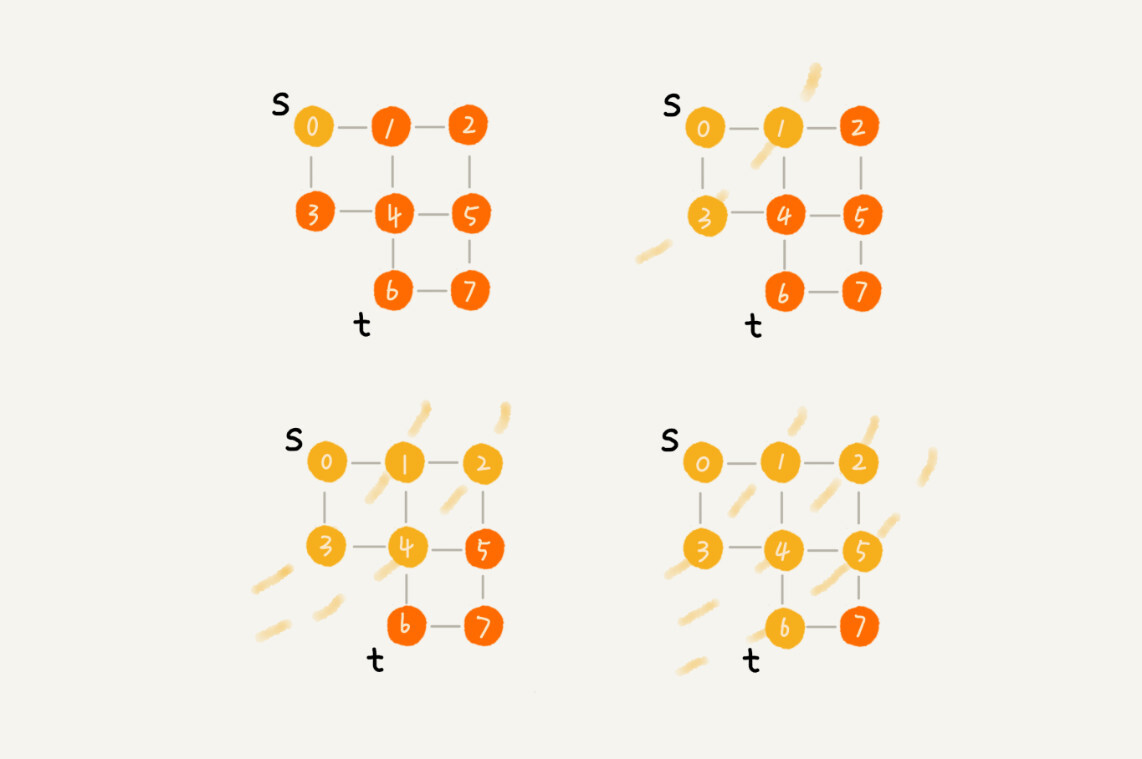
广度优先搜索，直观地讲其实就是一种地毯式层层推进的搜索策略，即先查找离起始顶点最近的，然后是次近的，依次往外搜索。

广度优先搜索需要借助队列来实现，遍历得到的路径就是起始顶点到终止顶点的最短路径。

代码实现

尽管广度优先搜索的原理挺简单，但代码实现还是稍微有点复杂度。

// 广度优先搜索算法：s 表示起始顶点，t 表示终止顶点， 目标是找出从 s 到 t 的最短路径
public void bfs(int s, int t) {
    if (s == t) return;
    boolean[] visited = new boolean[v]; //用来记录已经被访问的顶点
    visited[s] = true;
    Queue<Integer> queue = new LinkedList<>();
    queue.add(s);
    int[] prev = new int[v];
    for (int i = 0; i < v; ++i) {
        prev[i] = -1;
    }
    while (queue.size() != 0) {
        int w = queue.poll();
        for (int i = 0; i < adj[w].size(); ++i) {
            int q = adj[w].get(i);
            if (!visited[q]) {
                prev[q] = w;
                if (q == t) {
                    print(prev, s, t);
                    return;
                }
                visited[q] = true;
                queue.add(q);
            }
        }
    }
}

private void print(int[] prev, int s, int t) {
    if (prev[t] != -1 && t != s) {
        print(prev, s, prev[t]); // 递归打印 s->t 的路径
    }
    System.out.print(t + " ");
}

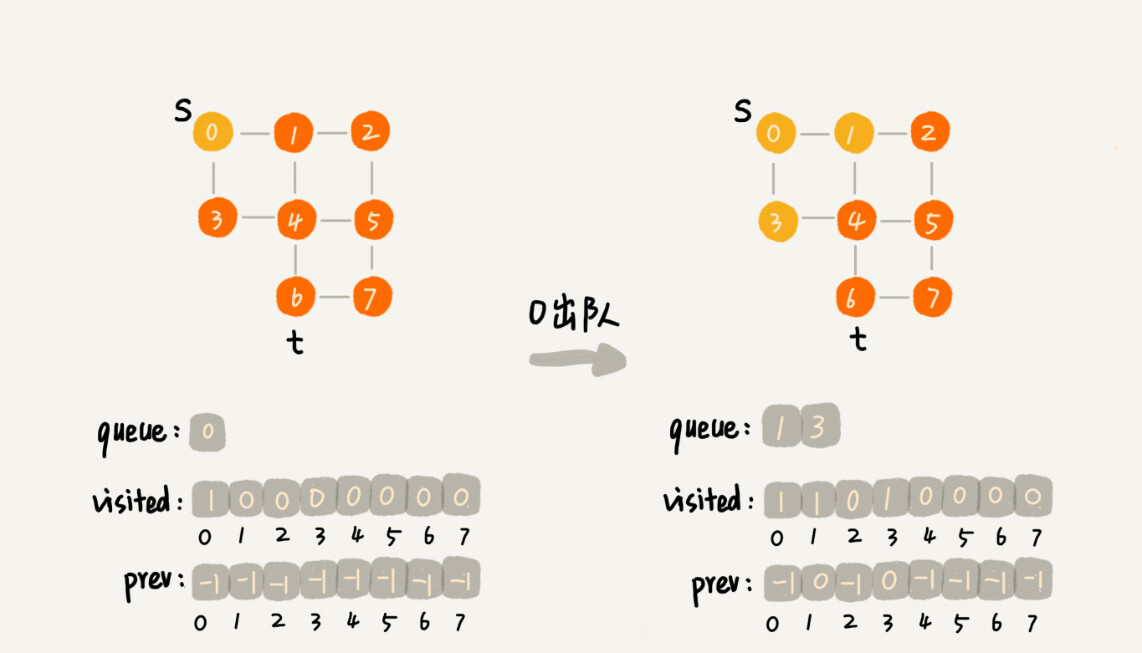
里面有三个重要的辅助变量 visited、queue、prev

• visited 是用来记录已经被访问的顶点，用来避免顶点被重复访问。如果顶点 q 被访问，那相应的 visited[q] 会被设置为 true。
• queue 是一个队列，用来存储已经被访问、但相连的顶点还没有被访问的顶点。因为广度优先搜索是逐层访问的，也就是说，我们只有把第 k 层的顶点都访问完成之后，才能访问第 k+1 层的顶点。当我们访问到第 k 层的顶点的时候，我们需要把第 k 层的顶点记录下来，稍后才能通过第 k 层的顶点来找第 k+1 层的顶点。所以，我们用这个队列来实现记录的功能。
• prev 用来记录搜索路径。当我们从顶点 s 开始，广度优先搜索到顶点 t 后，prev 数组中存储的就是搜索的路径。不过，这个路径是反向存储的。prev[w] 存储的是，顶点 w 是从哪个前驱顶点遍历过来的。比如，我们通过顶点 2 的邻接表访问到顶点 3，那 prev[3] 就等于 2。为了正向打印出路径，我们需要递归地来打印，具体可以看下 print() 函数的实现方式。

分解示意图

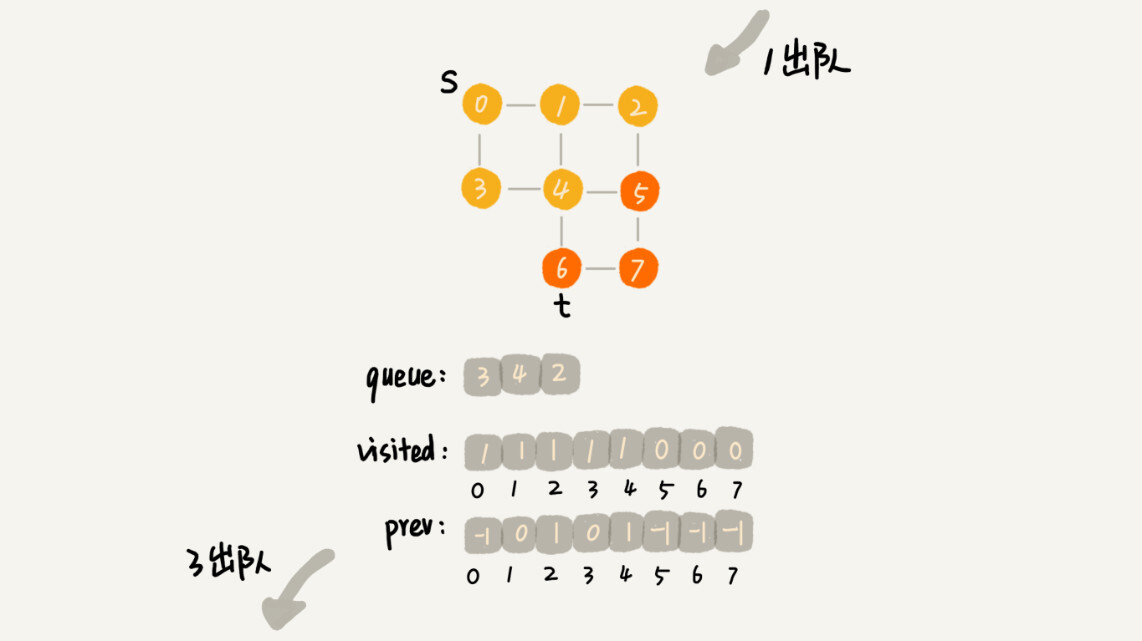
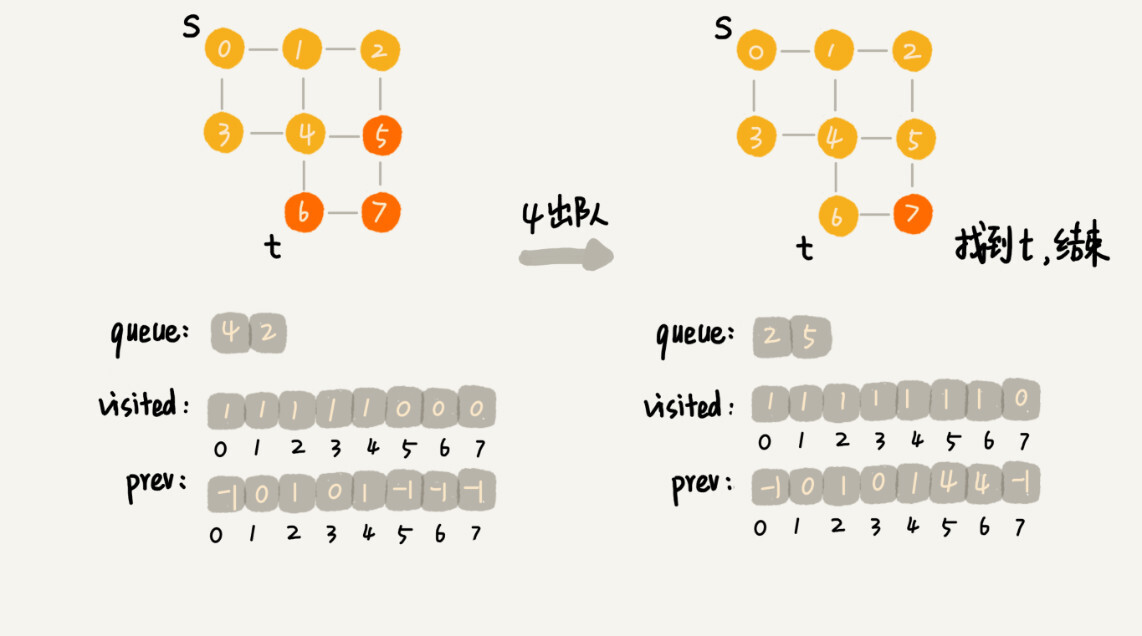
复杂度分析

最坏情况下，终止顶点 t 离起始顶点 s 很远，需要遍历完整个图才能找到。这个时候，每个顶点都要进出一遍队列，每个边也都会被访问一次，所以，广度优先搜索的时间复杂度是 O(V+E)，其中，V 表示顶点的个数，E 表示边的个数。

树的特性是 E = V - 1，树是边最少的联通图，对于一个连通图来说 E >= V -1。所以，广度优先搜索的时间复杂度也可以简写为 O(E)。

广度优先搜索的空间消耗主要在几个辅助变量 visited 数组、queue 队列、prev 数组上。这三个存储空间的大小都不会超过顶点的个数，所以空间复杂度是 O(V)。

深度优先搜索 DFS

深度优先搜索（Depth-First-Search），简称 DFS。

深度优先搜索用的是回溯思想，非常适合用递归实现。换种说法，深度优先搜索是借助栈来实现的。

案例：走迷宫

最直观的例子就是走迷宫。假设你站在迷宫的某个岔路口，然后想找到出口。你随意选择一个岔路口来走，走着走着发现走不通的时候，你就回退到上一个岔路口，重新选择一条路继续走，直到最终找到出口。这种走法就是一种深度优先搜索策略。

下图示例了利用 DFS 遍历的路径。这里面实线箭头表示遍历，虚线箭头表示回退。

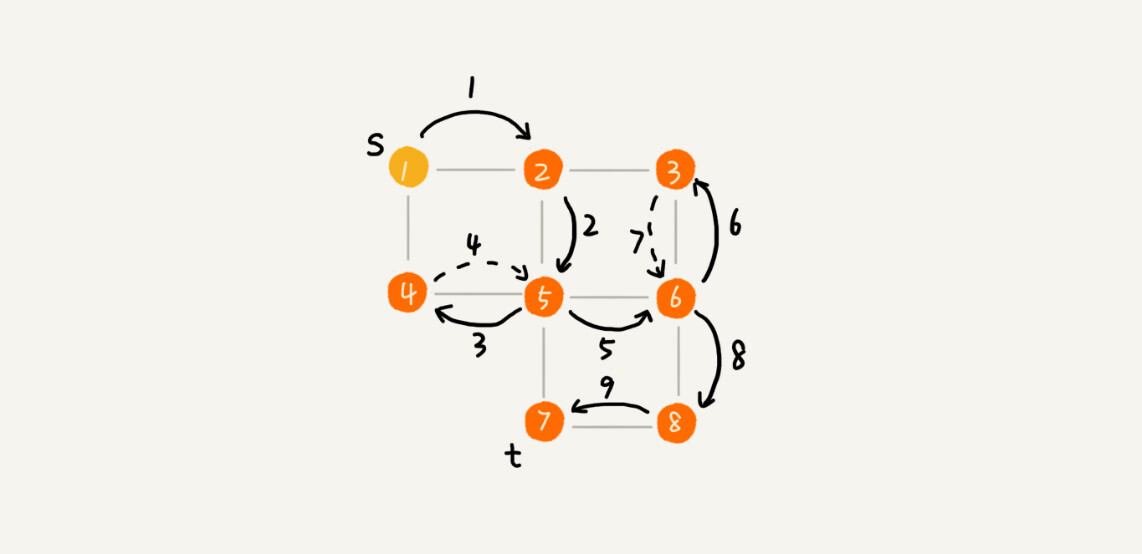
从图中我们可以看出，深度优先搜索找出来的路径，并 不是 顶点 s 到顶点 t 的最短路径。

代码实现

如何在图中寻找一条从顶点 s 到顶点 t 的路径？映射到迷宫那个例子，s 就是你起始所在的位置，t 就是出口。

boolean found = false; // 全局变量或者类成员变量

public void dfs(int s, int t) {
    found = false;
    boolean[] visited = new boolean[v];
    int[] prev = new int[v];
    for (int i = 0; i < v; ++i) {
        prev[i] = -1;
    }
    recurDfs(s, t, visited, prev);
    print(prev, s, t);
}

private void recurDfs(int w, int t, boolean[] visited, int[] prev) {
    if (found == true) return;
    visited[w] = true;
    if (w == t) {
        found = true;
        return;
    }
    for (int i = 0; i < adj[w].size(); ++i) {
        int q = adj[w].get(i);
        if (!visited[q]) {
            prev[q] = w;
            recurDfs(q, t, visited, prev); //递归
        }
    }
}

深度优先搜索代码实现也用到了 prev、visited 变量以及 print() 函数，它们跟广度优先搜索代码实现里的作用是一样的。

不过，深度优先搜索代码实现里，有个比较特殊的变量 found，它的作用是，当我们已经找到终止顶点 t 之后，我们就不再递归地继续查找了。

复杂度分析

从我前面画的图可以看出，每条边最多会被访问两次，一次是遍历，一次是回退。所以，图上的深度优先搜索算法的时间复杂度是 O(E)，E 表示边的个数。

深度优先搜索算法的消耗内存主要是 visited、prev 数组和递归调用栈。visited、prev 数组的大小跟顶点的个数 V 成正比，递归调用栈的最大深度不会超过顶点的个数，所以总的空间复杂度就是 O(V)。

如何找出社交网络中用户的三度好友关系

这个问题非常适合用图的广度优先搜索算法来解决，因为广度优先搜索是层层往外推进的。

• 首先，遍历与起始顶点最近的一层顶点，也就是用户的一度好友
• 然后再遍历与用户距离的边数为 2 的顶点，也就是二度好友关系
• 然后再遍历与用户距离的边数为 3 的顶点，也就是三度好友关系

我们只需要稍加改造一下广度优先搜索代码，用一个数组来记录每个顶点与起始顶点的距离，非常容易就可以找出三度好友关系。

也可以用 DFS，递归时传多一个离初始节点的距离值，访问节点时，距离超过 3 则不再继续递归

内容小结

广度优先搜索 BFS 和深度优先搜索 DFS 是图上的两种最常用、最基本的搜索算法，比起其他高级的搜索算法，比如 A*、IDA*等要简单粗暴，没有什么优化，所以，也被叫作暴力搜索算法。这两种搜索算法仅适用于状态空间不大，也就是说图不大的搜索。

广度优先搜索，通俗的理解就是，地毯式层层推进，从起始顶点开始，依次往外遍历。广度优先搜索需要借助队列来实现，遍历得到的路径就是起始顶点到终止顶点的最短路径。

深度优先搜索用的是回溯思想，非常适合用递归实现。换种说法，深度优先搜索是借助栈来实现的。

在执行效率方面，深度优先和广度优先搜索的时间复杂度都是 O(E)，空间复杂度是 O(V)。

2021-09-12