数据结构与算法之美-7 二分查找 跳表
目录
15 | 二分查找（上）：如何用最省内存的方式实现快速查找功能？
二分查找针对的是一个有序的数据集合，查找思想有点类似分治思想。每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为 0。
logn 是一个非常“恐怖”的数量级，即便 n 非常非常大，对应的 logn 也很小。比如 n 等于 2 的 32 次方，大约是 42 亿，如果我们在 42 亿个数据中用二分查找一个数据，最多需要比较 32 次。
二分查找的非递归实现
假设有序数组中
不存在重复元素
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = (low + high) / 2;
if (a[mid] == value) {
return mid;
} else if (a[mid] < value) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return -1;
}
容易出错的 3 个地方
- 循环退出条件：注意是
low <= high，而不是low < high - mid 的取值：
- 上述代码中
mid = (low + high) / 2这种写法是有问题的，因为两者之和有可能会溢出 - 改进的方法一：
mid = low + (high - low) / 2 - 改进的方法二：
mid = low + (high - low) >> 1
- 上述代码中
- low 和 high 的更新：
- 正确为：
low = mid + 1，high = mid - 1 - 这里如果不 +1 或 -1，就可能会发生死循环
- 正确为：
二分查找的递归实现
// 二分查找的递归实现
public int bsearch(int[] a, int n, int val) {
return bsearchInternally(a, 0, n - 1, val);
}
private int bsearchInternally(int[] a, int low, int high, int value) {
if (low > high) {
return -1;
}
int mid = low + ((high - low) >> 1);
if (a[mid] == value) {
return mid;
} else if (a[mid] < value) {
return bsearchInternally(a, mid + 1, high, value);
} else {
return bsearchInternally(a, low, mid - 1, value);
}
}
二分查找应用场景的局限性
- 首先，二分查找依赖的是
顺序表结构，简单点说就是数组- 主要原因是二分查找算法需要按照下标
随机访问元素
- 主要原因是二分查找算法需要按照下标
- 其次，二分查找针对的是
有序数据- 如果我们针对的是一组
静态的数据，没有频繁地插入、删除，我们可以进行一次排序，多次二分查找。这样排序的成本可被均摊，二分查找的边际成本就会比较低。 - 但是，如果我们的数据集合有频繁的插入和删除操作，针对这种动态数据集合，无论哪种方法，维护有序的成本都是很高的。
- 二分查找只能用在插入、删除操作不频繁，一次排序多次查找的场景中。针对动态变化的数据集合，二分查找将不再适用。
- 如果我们针对的是一组
- 再次，数据量
太小不适合二分查找- 如果要处理的数据量很小，完全没有必要用二分查找，顺序遍历就足够了
- 最后，数据量太大也不适合二分查找
- 二分查找的底层需要依赖
数组这种数据结构，而数组为了支持随机访问的特性，要求内存空间连续，对内存的要求比较苛刻。
- 二分查找的底层需要依赖
大部分情况下，用二分查找可以解决的问题，用散列表、二叉树都可以解决。但是，缺点是他们都会需要比较多的额外的内存空间。二分查找底层依赖的是数组，除了数据本身之外，不需要额外存储其他信息，是最省内存空间的存储方式。
16 | 二分查找（下）：如何快速定位IP对应的省份地址？
大部分情况下，用二分查找可以解决的问题，用散列表、二叉树都可以解决。但是二分查找更适合用在近似查找问题，比如今天讲的这几种变体问题，用其他数据结构，比如散列表、二叉树，就比较难实现了。
查找第一个值等于给定值的元素
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else if (a[mid] < value) {
low = mid + 1;
} else {
if (mid == 0 || a[mid - 1] != value) {
return mid;
} else {
high = mid - 1;
}
}
}
return -1;
}
当 a[mid]=value 的时候，我们需要确认一下这个 a[mid] 是不是第一个值等于给定值的元素：
- 如果 mid 等于 0，那这个元素已经是数组的第一个元素，那它肯定是我们要找的
- 如果 mid 不等于 0，但
a[mid]的前一个元素a[mid-1]不等于 value，那也说明a[mid]就是我们要找的第一个值等于给定值的元素 - 如果经过检查之后发现
a[mid]前面的一个元素a[mid-1]也等于 value，那说明此时的a[mid]肯定不是我们要查找的第一个值等于给定值的元素。那我们就更新high=mid-1，因为要找的元素肯定出现在[low, mid-1]之间。
查找最后一个值等于给定值的元素
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else if (a[mid] < value) {
low = mid + 1;
} else {
if (mid == n - 1 || a[mid + 1] != value) {
return mid;
} else {
low = mid + 1;
}
}
}
return -1;
}
查找第一个大于等于给定值的元素
public int bsearch(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] >= value) {
if (mid == 0 || a[mid - 1] < value) {
return mid;
} else {
high = mid - 1;
}
} else {
low = mid + 1;
}
}
return -1;
}
查找最后一个小于等于给定值的元素
public int bsearch7(int[] a, int n, int value) {
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = low + ((high - low) >> 1);
if (a[mid] > value) {
high = mid - 1;
} else {
if (mid == n - 1 || a[mid + 1] > value) {
return mid;
} else {
low = mid + 1;
}
}
}
return -1;
}
如何快速定位出一个 IP 地址的归属地
如果 IP 区间与归属地的对应关系不经常更新，我们可以先预处理这 12 万条数据，让其按照起始 IP 从小到大排序。
如何来排序呢？我们知道，IP 地址可以转化为 32 位的整型数。所以，我们可以将起始地址，按照对应的整型值的大小关系，从小到大进行排序。然后，这个问题就可以转化为我刚讲的第四种变形问题“在有序数组中，查找最后一个小于等于某个给定值的元素”了。
当我们要查询某个 IP 归属地时，我们可以先通过二分查找，找到最后一个起始 IP 小于等于这个 IP 的 IP 区间，然后，检查这个 IP 是否在这个 IP 区间内，如果在，我们就取出对应的归属地显示；如果不在，就返回未查找到。
17 | 跳表：为什么Redis一定要用跳表来实现有序集合？
因为二分查找底层依赖的是数组随机访问的特性，所以只能用数组来实现。如果数据存储在链表中，我们只需要对链表稍加改造，就可以支持类似二分的查找算法。我们把改造之后的数据结构叫做跳表(Skip list)。
跳表是一种各方面性能都比较优秀的动态数据结构，可以支持快速地插入、删除、查找操作，写起来也不复杂，甚至可以替代红黑树(Red-black tree)。
跳表的结构
跳表就是链表加多级索引的结构
- 对链表每两个结点提取一个结点到上一级，抽出来的那一级叫做索引或索引层
- 在第一级索引的基础之上，每两个结点就抽出一个结点到第二级索引
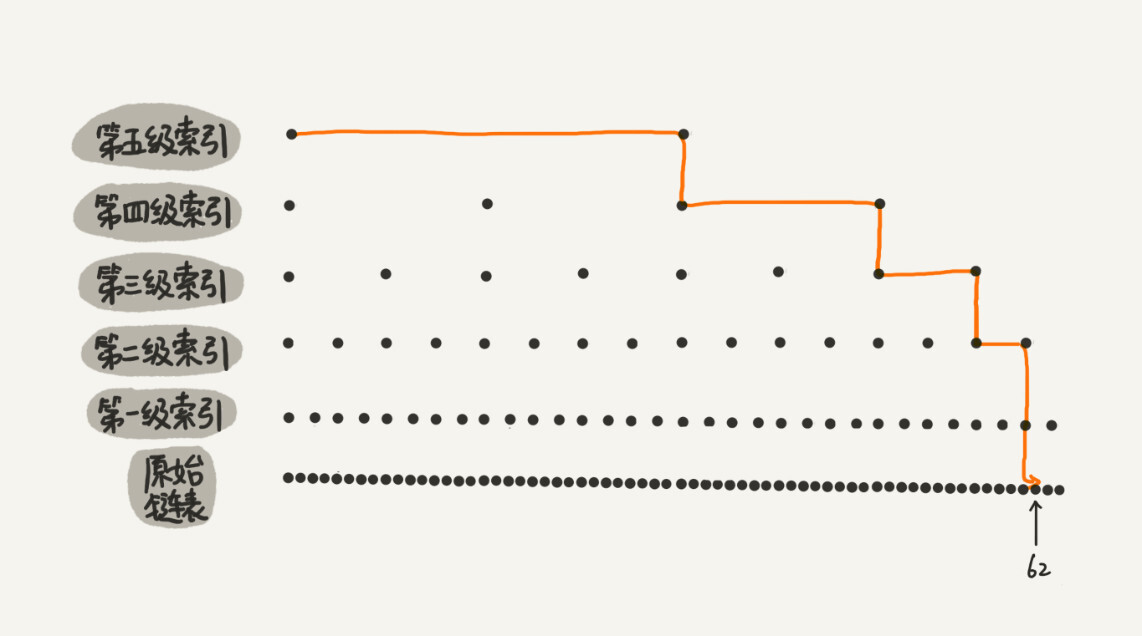
从图中我们可以看出，原来没有索引的时候，查找 62 需要遍历 62 个结点，现在只需要遍历 11 个结点
跳表的时间复杂度
如果链表里有 n 个结点，会有多少级索引呢？
- 每两个结点会抽出一个结点作为上一级索引的结点，那第一级索引的结点个数大约就是
n/2，第二级索引的结点个数大约就是n/4，第三级索引的结点个数大约就是n/8，依次类推，也就是说，第 k 级索引的结点个数是第k-1级索引的结点个数的1/2，那第 k级索引结点的个数就是n/(2^k)。 - 假设索引有 h 级，最高级的索引有 2 个结点。通过上面的公式，我们可以得到
n/(2^h)=2，从而求得h=logn-1。如果包含原始链表这一层，整个跳表的高度就是logn。 - 我们在跳表中查询某个数据的时候，如果每一层都要遍历 m 个结点，那在跳表中查询一个数据的时间复杂度就是
O(m*logn)。 - 那这个 m 的值是多少呢？按照前面这种索引结构，我们每一级索引都最多只需要遍历 3 个结点，也就是说
m=3。
所以在跳表中查询任意数据的时间复杂度就是 O(logn)
跳表的空间复杂度
假设原始链表大小为 n，那第一级索引大约有 n/2 个结点，第二级索引大约有 n/4 个结点，以此类推，每上升一级就减少一半，直到剩下 2 个结点。如果我们把每层索引的结点数写出来，就是一个等比数列。这几级索引的结点总和就是 n/2+n/4+n/8…+8+4+2 = n-2
所以，跳表的空间复杂度是 O(n)
我们前面都是每两个结点抽一个结点到上级索引，如果我们每三个结点抽一个结点到上级索引，通过等比数列求和公式，总的索引结点大约就是 n/3+n/9+n/27+...+9+3+1 = n/2。尽管空间复杂度还是 O(n)，但比上面的每两个结点抽一个结点的索引构建方法，要减少了一半的索引结点存储空间。
实际上，在软件开发中，我们不必太在意索引占用的额外空间。因为原始链表中存储的有可能是很大的对象，而索引结点只需要存储关键值和几个指针，并不需要存储对象，所以当对象比索引结点大很多时，那索引占用的额外空间就可以忽略了。
高效的动态插入和删除
跳表不仅支持O(logn)时间复杂度的查找操作，还支持O(logn)时间复杂度的动态的插入、删除操作。
在单链表中，一旦定位好要插入的位置，插入结点的时间复杂度就是 O(1)。但是，为了保证原始链表中数据的有序性，我们需要先找到要插入的位置，这个查找操作的时间复杂度就是前面讲过的O(logn)。
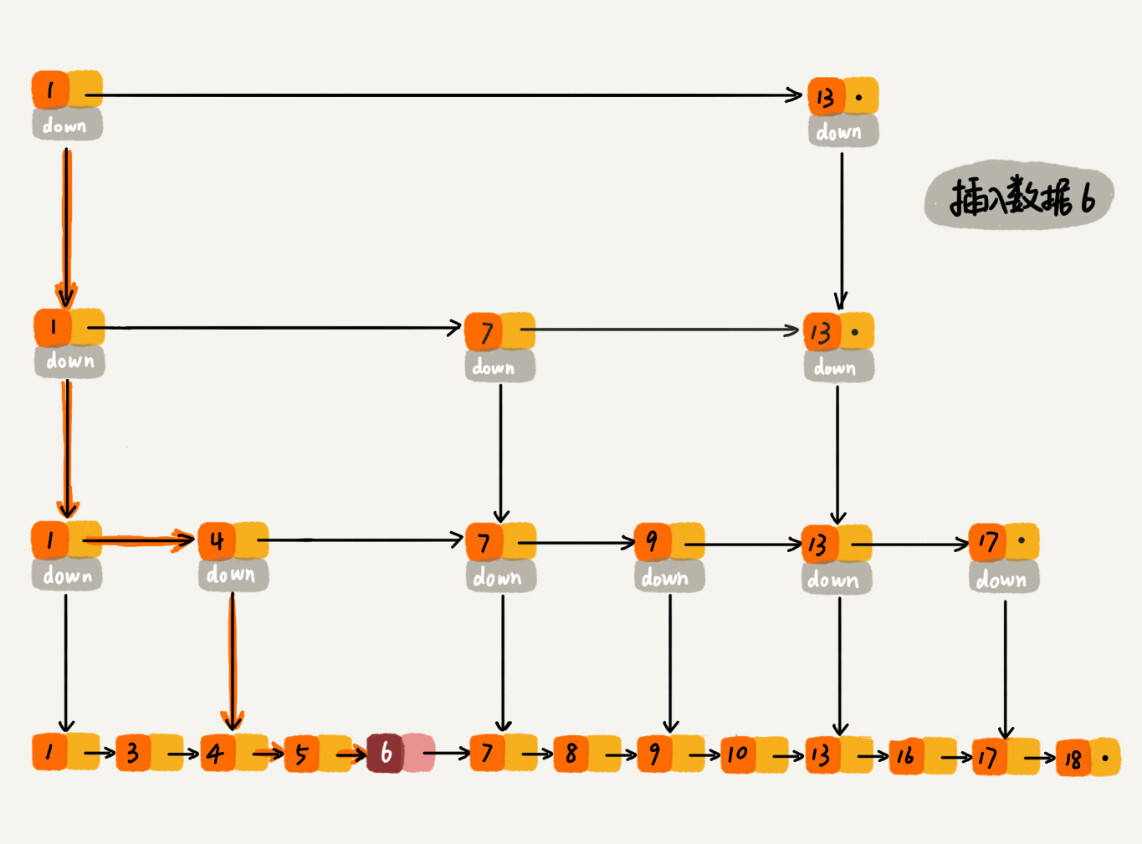
如果这个结点在索引中也有出现，我们除了要删除原始链表中的结点，还要删除索引中的。因为单链表中的删除操作需要拿到要删除结点的前驱结点，然后通过指针操作完成删除。所以在查找要删除的结点的时候，一定要获取前驱结点。当然，如果我们用的是双向链表，就不需要考虑这个问题了。
跳表索引动态更新
当我们不停地往跳表中插入数据时，如果我们不更新索引，就有可能出现某 2 个索引结点之间数据非常多的情况。极端情况下，跳表还会退化成单链表。
作为一种动态数据结构，我们需要某种手段来维护索引与原始链表大小之间的平衡，也就是说，如果链表中结点多了，索引结点就相应地增加一些，避免复杂度退化，以及查找、插入、删除操作性能下降。
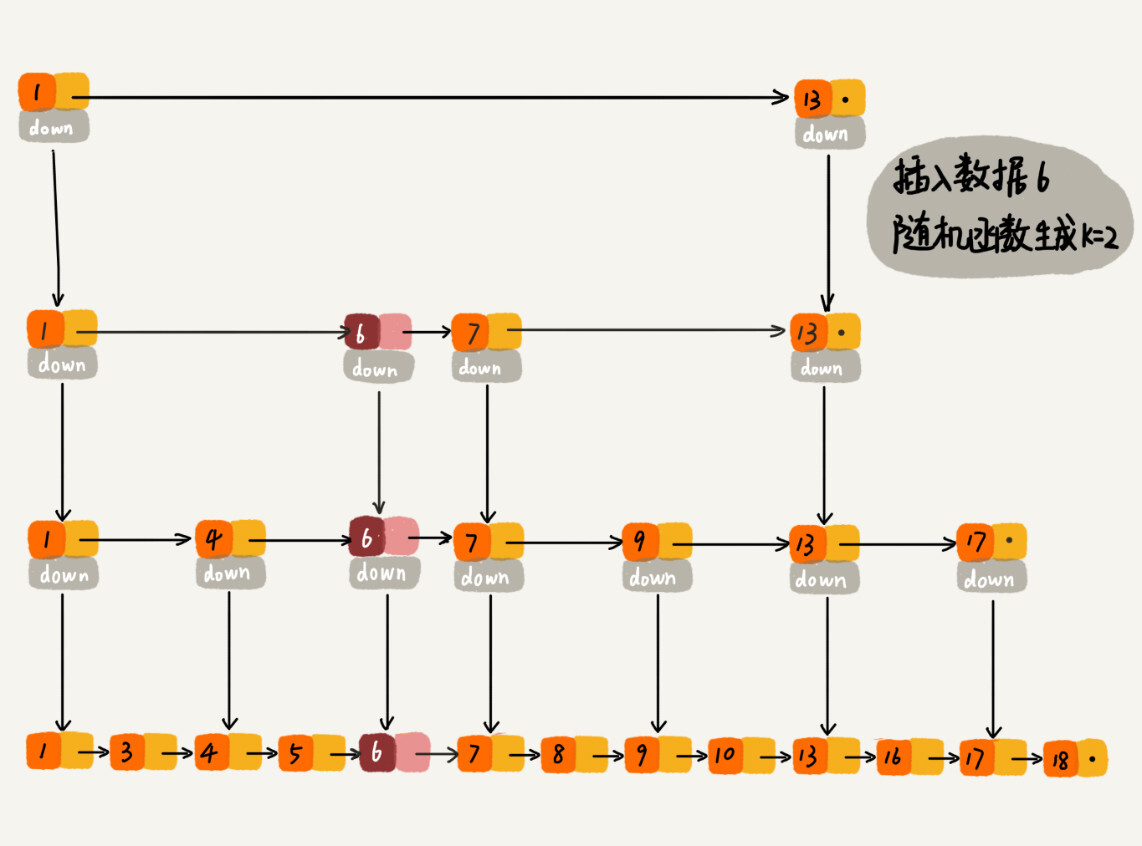
红黑树、AVL 树这样平衡二叉树是通过左右旋的方式保持左右子树的大小平衡，而跳表是通过随机函数来维护平衡性。
当我们往跳表中插入数据的时候，我们可以选择同时将这个数据插入到部分索引层中。
如何选择加入哪些索引层呢？我们通过一个随机函数，来决定将这个结点插入到哪几级索引中，比如随机函数生成了值 K，那我们就将这个结点添加到第一级到第 K 级这 K 级索引中。
解答开篇
Redis 中的有序集合是通过跳表来实现的(严格点讲，其实还用到了散列表)。如果你去查看 Redis 的开发手册，就会发现，Redis 中的有序集合支持的核心操作主要有下面这几个：
- 插入一个数据
- 删除一个数据
- 查找一个数据
- 迭代输出有序序列
- 按照
区间查找数据
其中，插入、删除、查找以及迭代输出有序序列这几个操作，红黑树也可以完成，时间复杂度跟跳表是一样的。但是，按照区间来查找数据这个操作，红黑树的效率没有跳表高。
对于按照区间查找数据这个操作，跳表可以做到 O(logn) 的时间复杂度定位区间的起点，然后在原始链表中顺序往后遍历就可以了。
其他原因：
- 跳表代码相比红黑树更容易实现，可读性好，不容易出错
- 跳表更加灵活，它可以通过改变索引构建策略，有效平衡执行效率和内存消耗
缺点：跳表并没有一个现成的实现，在开发中，如果你想使用跳表，必须要自己实现。
2021-8-23
本文来自博客园，作者：白乾涛，转载请注明原文链接：https://www.cnblogs.com/baiqiantao/p/15175963.html
