End

二叉树 遍历 先序 中序 后序 深度 广度

本文地址

目录

目录

二叉树遍历

测试案例

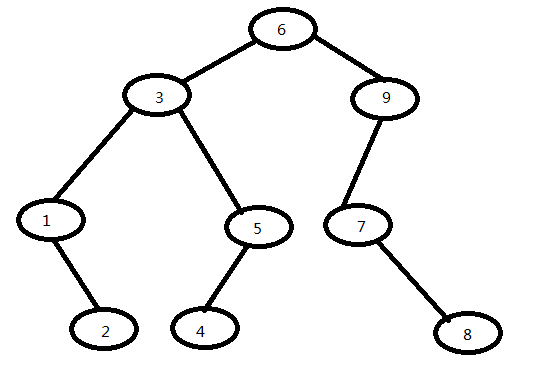
遍历结果：

先序遍历：631254978
中序遍历：123456789
后序遍历：214538796
广度优先：639157248

构造二叉树

public static Node init() {
    //注意必须逆序建立，先建立子节点，再逆序往上建立，因为非叶子结点会使用到下面的节点 
    Node J = new Node(8, null, null);
    Node H = new Node(4, null, null);
    Node G = new Node(2, null, null);
    
    Node F = new Node(7, null, J);
    Node E = new Node(5, H, null);
    Node D = new Node(1, null, G);
    
    Node C = new Node(9, F, null);
    Node B = new Node(3, D, E);
    
    Node A = new Node(6, B, C);
    return A; //返回根节点  
}

结点定义

class Node {
    public int value;
    public Node left;
    public Node right;

    public Node(int value, Node left, Node right) {
        this.value = value;
        this.left = left;
        this.right = right;
    }
}

使用递归遍历

其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次。

public static void preOrderTraversal(Node root) {
    if (root != null) {
        System.out.print(root.value); //先(根)序遍历
        preOrderTraversal(root.left); //递归遍历左孩子
        preOrderTraversal(root.right); //递归遍历右孩子
    }
}

public static void inOrderTraversal(Node root) {
    if (root != null) {
        inOrderTraversal(root.left);
        System.out.print(root.value); //中(根)序遍历
        inOrderTraversal(root.right);
    }
}

public static void postOrderTraversal(Node root) {
    if (root != null) {
        postOrderTraversal(root.left);
        postOrderTraversal(root.right);
        System.out.print(root.value); //后(根)序遍历
    }
}

使用栈遍历

public static void preOrderTraversalStack(Node root) {
    Stack<Node> stack = new Stack<>();
    while (root != null || !stack.isEmpty()) {
        if (root != null) {
            System.out.print(root.value); //压栈之前先访问，先序遍历
            stack.push(root); //压栈
            root = root.left; //访问左叶子节点
        } else { //没有左(右)叶子节点
            root = stack.pop(); //返回最近压入栈的结点【核心】
            root = root.right; //访问右叶子节点
        }
    }
}

public static void preOrderTraversalStack2(Node root) {
    Stack<Node> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        Node node = stack.pop();
        System.out.print(node.value); //先序遍历
        if (node.right != null) {
            stack.push(node.right);
        }
        if (node.left != null) {
            stack.push(node.left);
        }
    }
}

public static void inOrderTraversalStack(Node root) {
    Stack<Node> stack = new Stack<>();
    Node node = root;
    while (node != null || !stack.isEmpty()) {
        if (node != null) {
            stack.push(node);
            node = node.left;
        } else {
            node = stack.pop();
            System.out.print(node.value); //中序遍历
            node = node.right;
        }
    }
}

public static void postOrderTraversalStack(Node root) {
    Stack<Node> stack = new Stack<>();
    Stack<Node> output = new Stack<>();//构造一个中间栈来存储逆后序遍历的结果
    Node node = root;
    while (node != null || !stack.isEmpty()) {
        if (node != null) {
            output.push(node);
            stack.push(node);
            node = node.right;
        } else {
            node = stack.pop();
            node = node.left;
        }
    }
    while (!output.isEmpty()) {
        System.out.print(output.pop().value); //后序遍历
    }
}

又叫宽度优先搜索，或横向优先搜索。
对每一层节点依次访问，访问完一层进入下一层，而且每个节点只能访问一次

public static void levelTraversal(Node root) {
    Queue<Node> queue = new LinkedList<>(); //LinkedList是Java中最普通的一个队列
    queue.offer(root); //add、addLast
    while (!queue.isEmpty()) {
        Node node = queue.poll();//removeFirst
        if (node != null) {
            System.out.print(node.value);
            queue.offer(node.left);
            queue.offer(node.right);
        }
    }
}

2018-12-8

posted @ 2018-12-08 14:47  白乾涛  阅读(513)  评论(0)  编辑  收藏  举报