利用python 学习数据分析 (学习三)

内容学习自:

Python for Data Analysis, 2nd Edition        

就是这本

纯英文学的很累,对不对取决于百度翻译了

前情提要:

各种方法贴:

　　https://www.cnblogs.com/baili-luoyun/p/10250177.html

　　　本节内容,numpy 结尾, 以及pands初入门

　　　　　　一:伪随机函数

samples =np.random.normal(size=(3,3))
print(samples)
samples1 =np.random.seed(1234)  #调节随机种子
print(samples1)

>>>>

[[ 0.91041087  0.99724402 -0.0681944 ]
 [ 0.48277059 -1.50446272  0.30656754]
 [-0.01929894 -0.27835256 -0.68331925]]
None

 

　　　　　　       2>:给上下限的数取整

samplse1 = np.random.randint(1,6)   #给上下限的数取整数
print(samplse1)
.>>>.>>>>>
#  随机整数
2

　　

　　　　　　　　3>:产生正太分布样本

arr1 =np.random.randn(3,3)        #产生正态分布的样本值
print(arr1)


>>>>>
[[ 0.55526507 -0.3952732   1.49921319]
 [-0.06943318 -0.05375604 -0.26636376]
 [-1.48909115 -0.00702559  0.15973251]]

 

 

　　　　　　　　4>:产生均匀分布样本

arr1 =np.random.rand(3,3)       #产生均匀分布的样本质
print(arr1)
>>>
[[0.56847387 0.23533505 0.97136229]
 [0.0049996  0.60753788 0.20997453]
 [0.41777576 0.26264969 0.55777828]]

 

 

 　　　　二:随机漫步

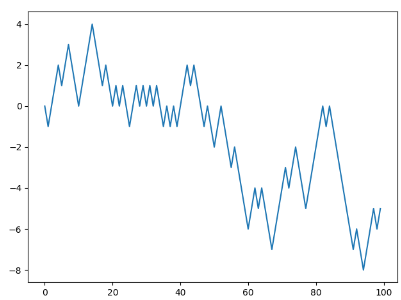
　　　　　　1:单随机漫步(普通方法)

import matplotlib.pylab as plt
import random
postition = 0
walk =[postition]
steps =1000
for i in range(steps):
    step = 1 if random.randint(0,1) else -1
    postition += step
    walk.append(postition)
print(walk)
plt.plot(walk[:100])
plt.show()

>>>>>>
[0, 1, 0, 1, 2, 1, 0, -1, 0, -1, -2, -3, -4, -5, -6, -5, -6, -5, -6, -7, -8, -7, -8, -7, -8, -7, -6, -5, -6, -7, -6, -7, -8, -7, -8, -9, -8, -7, -6, -5, -6, -5, -4, -3, -4, -3, -2, -3, -4, -5, -4, -5, -4, -5, -6, -5, -4, -3, -4, -5, -4, -3, -2, -3, -2, -1, -2, -1, -2, -3, -4, -5, -4, -3, -2, -3, -4, -3, -2, -1, 0, 1, 0, -1, 0, -1, 0, 1, 2, 3, 4, 5, 4, 3, 2, 3, 2, 1, 2, 1, 0, 1, 2, 3, 4, 3, 4, 3, 4, 3, 4, 3, 4, 5, 4, 5, 6, 7, 6, 5, 4, 3, 2, 1, 2, 3, 4, 3, 4, 5, 6, 5, 4, 5, 4, 5, 6, 5, 6, 5, 4, 3, 2, 1, 2, 1, 0, 1, 0, -1, 0, 1, 0, -1, -2, -1, -2, -1, 0, 1, 2, 3, 4, 5, 4, 5, 4, 3, 4, 5, 6, 7, 8, 7, 6, 5, 4, 5, 6, 7, 6, 7, 6, 7, 8, 9, 10, 9, 8, 9, 8, 9, 10, 11, 10, 11, 12, 11, 10, 9, 10, 9, 8, 7, 8, 7, 6, 5, 4, 5, 4, 3, 2, 1, 0, 1, 0, 1, 2, 1, 0, -1, 0, -1, -2, -3, -2, -1, 0, 1, 0, 1, 0, -1, 0, 1, 0, -1, -2, -3, -2, -3, -2, -3, -4, -3, -2, -3, -4, -3, -2, -3, -4, -3, -4, -3, -2, -3, -4, -3, -4, -5, -6, -7, -6, -7, -8, -9, -10, -9, -8, -7, -8, -9, -10, -11, -12, -13, -14, -15, -14, -15, -14, -15, -14, -13, -12, -13, -14, -13, -14, -15, -16, -17, -18, -17, -18, -19, -18, -19, -20, -19, -18, -17, -16, -15, -14, -13, -12, -11, -12, -13, -12, -13, -12, -11, -10, -9, -8, -9, -8, -7, -8, -9, -10, -9, -10, -11, -12, -13, -12, -13, -14, -13, -12, -13, -14, -15, -14, -13, -12, -11, -12, -13, -12, -13, -12, -13, -14, -13, -14, -15, -14, -15, -16, -17, -16, -15, -16, -15, -16, -15, -16, -17, -18, -17, -18, -19, -18, -17, -16, -15, -14, -15, -14, -15, -16, -17, -18, -19, -20, -21, -20, -21, -20, -19, -20, -19, -18, -19, -18, -17, -16, -17, -16, -15, -16, -15, -14, -15, -14, -15, -14, -15, -16, -15, -14, -15, -16, -17, -16, -15, -16, -15, -16, -17, -16, -15, -14, -13, -14, -15, -14, -13, -14, -15, -16, -17, -16, -15, -14, -13, -12, -13, -14, -15, -14, -15, -14, -13, -12, -11, -12, -11, -12, -13, -14, -13, -12, -13, -12, -13, -14, -13, -14, -15, -14, -15, -14, -13, -12, -13, -14, -15, -14, -15, -16, -15, -16, -17, -18, -17, -18, -17, -18, -17, -18, -17, -18, -19, -18, -19, -18, -17, -18, -19, -20, -19, -18, -19, -18, -17, -16, -15, -14, -15, -16, -15, -14, -15, -16, -15, -16, -15, -14, -13, -12, -11, -12, -11, -10, -11, -12, -13, -14, -13, -12, -11, -10, -11, -10, -11, -12, -13, -14, -15, -14, -15, -14, -15, -16, -17, -16, -17, -18, -17, -18, -17, -16, -15, -14, -15, -14, -15, -16, -15, -14, -15, -16, -17, -18, -19, -20, -21, -20, -19, -18, -19, -18, -17, -18, -19, -18, -19, -18, -19, -20, -19, -18, -19, -20, -19, -20, -19, -18, -19, -20, -21, -22, -21, -22, -23, -22, -21, -20, -21, -20, -21, -22, -21, -20, -19, -18, -19, -18, -19, -18, -17, -18, -19, -20, -21, -20, -21, -22, -23, -24, -23, -22, -21, -20, -19, -20, -19, -18, -17, -18, -17, -18, -19, -20, -21, -20, -19, -18, -19, -20, -21, -22, -23, -22, -23, -22, -21, -20, -21, -22, -23, -24, -25, -24, -25, -24, -25, -24, -25, -26, -25, -24, -25, -26, -25, -26, -27, -28, -29, -30, -29, -30, -31, -32, -33, -34, -33, -32, -33, -34, -33, -34, -33, -32, -31, -30, -29, -30, -31, -30, -31, -30, -29, -28, -27, -26, -27, -28, -27, -26, -25, -24, -25, -26, -25, -24, -25, -24, -23, -22, -23, -22, -21, -20, -21, -20, -21, -20, -19, -20, -19, -20, -21, -22, -21, -20, -19, -20, -19, -18, -19, -18, -17, -16, -15, -16, -17, -18, -19, -20, -21, -22, -23, -22, -23, -24, -25, -26, -27, -28, -29, -28, -27, -28, -27, -26, -25, -24, -25, -26, -27, -26, -27, -26, -25, -24, -23, -24, -25, -24, -25, -26, -25, -26, -27, -28, -27, -26, -27, -26, -25, -24, -25, -26, -25, -26, -27, -28, -27, -28, -27, -26, -27, -26, -27, -26, -25, -24, -25, -24, -23, -22, -21, -20, -21, -20, -21, -22, -21, -20, -21, -20, -19, -20, -21, -20, -19, -20, -21, -22, -23, -24, -23, -22, -21, -22, -23, -24, -25, -26, -25, -24, -23, -24, -23, -22, -23, -22, -23, -22, -21, -20, -21, -22, -23, -24, -23, -22, -21, -22, -21, -22, -21, -20, -19, -20, -19, -20, -21, -22, -21, -20, -19, -18, -19, -18, -17, -18, -19, -20, -19, -20, -21, -20, -19, -20, -19, -18, -19, -20, -19, -20, -19, -18, -19, -18, -17, -18, -17, -18, -19, -18, -17, -16, -15, -16, -15, -16, -15, -14, -15, -16, -17, -18, -19, -20, -19, -18, -17, -16, -17, -18, -19, -20, -21, -20, -19, -20, -21, -20, -21, -20, -21, -22, -21, -20, -19, -20, -21, -20, -19, -20, -21, -22, -21, -22, -23, -24, -23, -24, -23, -24, -23, -24, -25, -26, -27, -28, -27, -28, -29, -30, -29, -28, -27, -26, -27, -26, -27, -28, -29, -28, -27, -26, -27, -28, -29, -30, -29, -30, -31, -32, -31, -32, -31, -30, -29, -30, -31, -30, -29, -28, -29, -30, -29, -28, -27, -28, -27, -26, -25, -26, -25, -26, -25, -24, -25, -26, -27, -26, -27, -26, -25, -24, -25, -26, -25, -24, -25, -24, -23, -22, -23, -24]

 

　　　　

 

 

　　　　　　2:利用numpy随机漫步

　　　　　　　　1>:生产1个0 或者1 的1维矩阵,1000次

nsteps =1000
draws =np.random.randint(0,2,size=nsteps)         #生成一个0 或者1 的1位矩阵,1000次
print(draws)
>>>>
[1 1 1 0 1 1 1 0 1 0 0 0 1 1 1 1 0 1 0 1 0 1 0 1 0 0 1 0 0 0 0 0 1 1 1 0 0.............. 0 1 1 1 0 1 1 1 1 1 1 0 1 0 0 1 0 1 1 1 0 0 0 1 0 1 0 0 0 0 1 0 0 1 1 0 1
 1]

 

 

 

　　　　　　　　2>:进行三元运算累加

 

nsteps =1000
draws =np.random.randint(0,2,size=nsteps)         #生成一个0 或者1 的1位矩阵,1000次
# print(draws)
steps =np.where(draws>0 ,1,-1)        #三元运算
walk =steps.cumsum()        #累加
print(walk)
plt.plot(walk)
plt.show()
>>>>>>>>>>
[  1   0  -1   0  -1   0  -1   0   1   0   1   2   3   4   3   4   5   6
   5   6   5   4   5   6   7   6   7   8   9  10  11  10  11  12  11  10
  11  12  11  12  11  12  13  14  13  12  13  14  15  16  15  16  17  18
  17  18  17  18  19  18  17  16  15  14  15  16  17  16  15  14  13  12
  11  10   9  10   9  10   9  10   9  10   9  10  11  10  11  12  11  10
   9  10  11  12  11  10   9  10  11  10   9   8   9   8   9   8   9   8
.......

 

 

 　　　　　　　　　　　　　　2.1>最大值  ,最小值

l1 =walk.min()            # 最小值
print(l1)
l2 =walk.max()               #最大值
print(l2)
>>>>>>
-51
12

　　　　　　　　

 　　　　　　　　　　　　　　　2.2>求距离0 到(+,-)10  距离最近的索引

 

l =(np.abs(walk)>=10).argmax()           #求距离0 位置10个距离的索引
print(l)
\>>>>>>>>>>>>>>
35

 

　　　　　　　　　　3:模拟多次随机漫步 

 

nwalks =5000    #组数
nsteps =1000    #步数
draws =np.random.randint(0,2,size=(nwalks,nsteps))   # 生成1,0 内的随机5000个漫步值
print(draws)
steps =np.where(draws>0 ,1,-1)
walks =steps.cumsum(1)
print(walks)
>>>>
[[1 1 1 ... 1 0 1]
 [0 0 0 ... 0 1 1]
 [1 0 0 ... 0 1 0]
 ...
 [0 0 0 ... 1 0 0]
 [1 1 0 ... 0 1 1]
 [1 0 1 ... 0 0 1]]
[[  1   2   3 ...  54  53  54]
 [ -1  -2  -3 ... -50 -49 -48]
 [  1   0  -1 ... -34 -33 -34]
 ...
 [ -1  -2  -3 ... -64 -65 -66]
 [  1   2   1 ...  -8  -7  -6]
 [  1   0   1 ...  -8  -9  -8]]