内容学习自:
Python for Data Analysis, 2nd Edition
就是这本
纯英文学的很累,对不对取决于百度翻译了
前情提要:
各种方法贴:
https://www.cnblogs.com/baili-luoyun/p/10250177.html
本内容主要讲的是:
继续数组和矢量
一:花式索引
定义:花式索引指的是利用整数进行索引,
假设我们有一个 8 *4的数组
arr = np.empty([8,4]) print(arr)#传入的元祖或者列表 for i in range(8): arr[i] =i print(arr)
>>>>>
[[4.67296746e-307 1.69121096e-306 1.29061074e-306 1.69119873e-306]
[1.78019082e-306 3.56043054e-307 7.56595733e-307 1.60216183e-306]
[8.45596650e-307 1.86918699e-306 1.78020169e-306 6.23054633e-307]
[1.95821439e-306 8.01097889e-307 1.78020169e-306 7.56601165e-307]
[1.02359984e-306 1.29060531e-306 1.24611741e-306 1.11261027e-306]
[7.56591659e-307 1.33511290e-306 6.89804133e-307 1.20160711e-306]
[6.89806849e-307 8.34446411e-308 1.22383391e-307 1.33511562e-306]
[1.42410974e-306 1.00132228e-307 1.33511969e-306 2.18568966e-312]]
>>>>> 赋值转换成这个
[[0. 0. 0. 0.]
[1. 1. 1. 1.]
[2. 2. 2. 2.]
[3. 3. 3. 3.]
[4. 4. 4. 4.]
[5. 5. 5. 5.]
[6. 6. 6. 6.]
[7. 7. 7. 7.]]
然后我拿 [3,4,5,4] 行
arr1 =arr[[3,4,5,4]] print(arr1) >>>>> [[0. 0. 0. 0.] [1. 1. 1. 1.] [2. 2. 2. 2.] [3. 3. 3. 3.] [4. 4. 4. 4.] [5. 5. 5. 5.] [6. 6. 6. 6.] [7. 7. 7. 7.]] >>>> [3,4,5,4] 拿3 4 5 4 行 [[3. 3. 3. 3.] [4. 4. 4. 4.] [5. 5. 5. 5.] [4. 4. 4. 4.]]
可以按照索引倒着拿 这次我拿 -1 -2 -3
arr2 =arr[[-1,-2,-3]] print(arr2) >>>>>>>>>>>> [[0. 0. 0. 0.] [1. 1. 1. 1.] [2. 2. 2. 2.] [3. 3. 3. 3.] [4. 4. 4. 4.] [5. 5. 5. 5.] [6. 6. 6. 6.] [7. 7. 7. 7.]] >>>>>>>>>> [[7. 7. 7. 7.] [6. 6. 6. 6.] [5. 5. 5. 5.]]
多维数组中拿到具体某行某列中的值
:>1 索引
:拿第1 ,4,3,2 行之后 ,拿第一行的0索引,第4行的第4个索引....
arr1 =np.arange(1,31).reshape(6,5) #指定范围1,31 内的 以6行5列显示 l1 =arr1[[1,4,3,2],[0,4,3,4]] print(arr1) print(l1)
>>>>>>
[[ 1 2 3 4 5]
[ 6 7 8 9 10]
[11 12 13 14 15]
[16 17 18 19 20]
[21 22 23 24 25]
[26 27 28 29 30]]
>>>>>>>>
[ 6 25 19 15]
>2:切片
arr1 =np.arange(1,31).reshape(6,5) #指定范围1,31 内的 以6行5列显示 # l1 =arr1[[1,4,3,2],[0,4,3,4]] print(arr1) # print(l1) l0 =arr1[[1,4,3,2]] print(l0) l1 =arr1[[1,4,3,2]][1:3,[0,3]] print(l1)
二:数组转置和轴的转换
1转置
arr = np.arange(1,16).reshape((3,5)) print(arr) arr1 =arr.T #把数组倒过来 print(arr1) >>>>> [[ 1 2 3 4 5] [ 6 7 8 9 10] [11 12 13 14 15]] >>>>>>>>>> [[ 1 6 11] [ 2 7 12] [ 3 8 13] [ 4 9 14] [ 5 10 15]]
arr = np.arange(1,17).reshape((2,2,4))
print(arr)
arr2 =arr.T #横纵轴转换
print(arr2)
>>>>>>>
[[[ 1 2 3 4]
[ 5 6 7 8]]
[[ 9 10 11 12]
[13 14 15 16]]]
>>>>>>>>>
[[[ 1 9]
[ 5 13]]
[[ 2 10]
[ 6 14]]
[[ 3 11]
[ 7 15]]
[[ 4 12]
[ 8 16]]]
2:矩阵的内积
arr =np.random.randn(6,3) # 随机获取一个 3 * 3 的矩阵 print(arr) arr1 =np.dot(arr.T,arr) #计算的内积 print(arr1)
>>>>>>>
[[-0.66062779 1.87683694 0.61244884]
[-0.05513691 -2.12443656 0.11384968]
[ 0.28945781 0.61337207 -0.1571619 ]
[-1.93240857 0.22642959 0.25642096]
[-0.34908123 0.53824799 1.59499567]
[ 0.12419976 1.16825608 -0.29790289]]
>>>>>>>>>>>>
[[ 4.39474115 -1.42556005 -1.54566235]
[-1.42556005 10.11777641 1.3797391 ]
[-1.54566235 1.3797391 3.11126421]]
3:矩阵的换行,转置
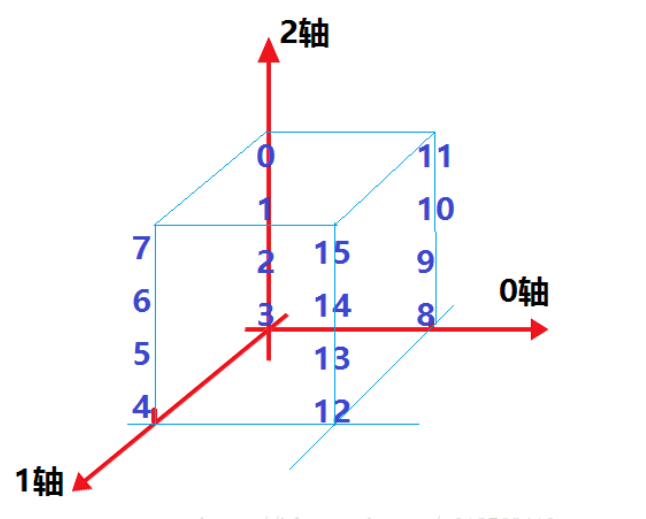
np.tranpose函数 的具体方法
https://blog.csdn.net/xiongchengluo1129/article/details/79017142
arr = np.arange(1,17).reshape((2,2,4)) print(arr)
arr1 =arr.transpose((1,0,2))
print(arr1)
l2 =arr.shape
print(l2)
>>
(2, 2, 4)
[[[ 1 2 3 4]
[ 5 6 7 8]]
[[ 9 10 11 12]
[13 14 15 16]]]
>>>>>>>
[[[ 1 2 3 4]
[ 9 10 11 12]]
[[ 5 6 7 8]
[13 14 15 16]]]
np.swapaxes() 转置函数
https://www.cnblogs.com/sunshinewang/p/6893503.html
arr2 =arr.swapaxes(1,2) print(arr2)
>>>>>>
[[[ 1 2 3 4]
[ 5 6 7 8]]
[[ 9 10 11 12]
[13 14 15 16]]]
[[[ 1 5]
[ 2 6]
[ 3 7]
[ 4 8]]
[[ 9 13]
[10 14]
[11 15]
[12 16]]]
三:直接调用函数进行运算
常用方法演示
1>开平方
arr =np.arange(1,10).reshape((3,3)) print(arr) l1 =np.sqrt(arr) #开平方 print(l1) >>>> [[1 2 3] [4 5 6] [7 8 9]] [[1. 1.41421356 1.73205081] [2. 2.23606798 2.44948974] [2.64575131 2.82842712 3. ]]
2>
arr =np.arange(1,10).reshape((3,3)) print(arr) l2 =np.exp(arr) print(l2) >>>>> [[1 2 3] [4 5 6] [7 8 9]] [[2.71828183e+00 7.38905610e+00 2.00855369e+01] [5.45981500e+01 1.48413159e+02 4.03428793e+02] [1.09663316e+03 2.98095799e+03 8.10308393e+03]]
3> 计算两组元素中最大的元素
maximun
arr1 =np.random.random(9).reshape(3,3) print(arr1) arr2 =np.random.random(9).reshape(3,3) print(arr2) l =np.maximum(arr1,arr2) print(l) >>>>> 第一组 [[0.80482431 0.81469155 0.00593739] [0.91246624 0.16354438 0.92251584] [0.10834283 0.47938184 0.99208569]] 第二组 [[0.38767246 0.30755364 0.42449632] [0.87273132 0.65693774 0.359721 ] [0.30002093 0.09380089 0.31326786]] 最大的 [[0.80482431 0.81469155 0.42449632] [0.91246624 0.65693774 0.92251584] [0.30002093 0.47938184 0.99208569]]
4:返回小数部分和整数部分
arr =np.random.randn(5)*5 print(arr) remainder,whole_part =np.modf(arr) print(remainder) #返回小数部分 print(whole_part) #返回整数部分 >>>>> 例子 [3.38825431 3.10743429 0.44134949 0.6804942 5.18949692] 小数 [0.38825431 0.10743429 0.44134949 0.6804942 0.18949692] 整数 [3. 3. 0. 0. 5.]


四:利用数组进行数据处理
接收两个一维数组并产生两个二维数组
arr1 = np.arange(-3,3) #-3 到3 每0.01 一个产生一维数组 print(arr1) xs ,ys=np.meshgrid(arr1,arr1) # 接受两个一维数组,并产生两个多维数组 print(ys) print(xs) >>>> [-3 -2 -1 0 1 2] [[-3 -3 -3 -3 -3 -3] [-2 -2 -2 -2 -2 -2] [-1 -1 -1 -1 -1 -1] [ 0 0 0 0 0 0] [ 1 1 1 1 1 1] [ 2 2 2 2 2 2]] [[-3 -2 -1 0 1 2] [-3 -2 -1 0 1 2] [-3 -2 -1 0 1 2] [-3 -2 -1 0 1 2] [-3 -2 -1 0 1 2] [-3 -2 -1 0 1 2]]
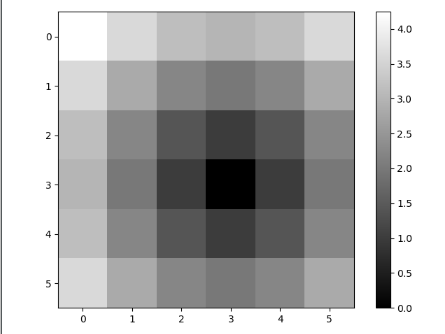
利用sqrt 处理后,输出图像
z =np.sqrt(xs**2+ys **2) print(z) plt.imshow(z,cmap=plt.cm.gray); plt.colorbar() plt.show() >>>>> [[4.24264069 3.60555128 3.16227766 3. 3.16227766 3.60555128] [3.60555128 2.82842712 2.23606798 2. 2.23606798 2.82842712] [3.16227766 2.23606798 1.41421356 1. 1.41421356 2.23606798] [3. 2. 1. 0. 1. 2. ] [3.16227766 2.23606798 1.41421356 1. 1.41421356 2.23606798] [3.60555128 2.82842712 2.23606798 2. 2.23606798 2.82842712]]
五:将条件逻辑转换为数组运算
np.where() #矢量化三元表达式
xarr =np.array([1.1,1.2,1.3,1.4,1.5]) yarr =np.array([2.1,2.2,2.3,2.4,2.5]) cond =np.array([True,False,True,True,False]) # result =[(x if c else y) for x,y,c in zip(xarr,yarr,cond)] # print(result) result =np.where(xarr,yarr,cond) print(result) >>>> [2.1 2.2 2.3 2.4 2.5]
arr =np.random.randn(4,4) # 生成一个随机的4x4素组 print(arr) # 让所有的数转化成bool 型 arr1 =arr>1 print(arr1) # 让所有的正数变成2 ,所有的负数变成-2 print(np.where(arr>0 ,2,arr)) #第一个是条件,之后是两个参数 >>>> [[-0.99386972 0.05822068 -0.7181413 -0.12671717] [-0.8489312 -1.04778749 1.74556603 0.6705986 ] [-0.02260339 -0.41670963 -0.44856615 -0.28767915] [ 0.90181549 1.13150798 1.85432972 -0.15670278]] [[False False False False] [False False True False] [False False False False] [False True True False]] [[-0.99386972 2. -0.7181413 -0.12671717] [-0.8489312 -1.04778749 2. 2. ] [-0.02260339 -0.41670963 -0.44856615 -0.28767915] [ 2. 2. 2. -0.15670278]]
六:数学和统计方法,以及简单的聚类
arr =np.arange(1,10).reshape(3,3) print(arr) print(arr.mean(axis=1)) # 求没行的平均值 print(np.mean(arr)) #求平均值 print(np.sum(arr))# 求和 >>>> [[1 2 3] [4 5 6] [7 8 9]] [2. 5. 8.] 5.0 45
一维累加
l =arr.cumsum() #累加函数 #[ 1 3 6 10 15 21 28] print(l) >>>> [ 1 3 6 10 15 21 28 36 45]
多维累加
arr1 =np.arange(1,10).reshape(3,3) print(arr1) arr2 =arr1.cumsum(axis =0) #0 是第一行不动后面行加上前面行 arr4 =arr1.cumsum() print(arr2) # print(arr4) arr3 =arr1.cumsum(axis =1) #1 是第一列不动,后面列加上前面列 print(arr3)
>>>>>>>
[[1 2 3]
[4 5 6]
[7 8 9]]
[[ 1 2 3]
[ 5 7 9]
[12 15 18]]
[[ 1 3 6]
[ 4 9 15]
[ 7 15 24]]

七:排序
>1:一维数组排序
# 一维数组 arr1 =np.random.randn(6) print(arr1) l1 =arr1.sort() #排序 print(arr1) >>>>>>>>>> 原数组 [-1.26064268 0.66278245 0.0403269 0.04349955 -0.60284353 0.653689 ] 排序后 [-1.26064268 -0.60284353 0.0403269 0.04349955 0.653689 0.66278245]
2:>多维数组的排序
arr2 =np.random.randn(3,3) print(arr2) arr2.sort(1)# 排序 可以横向和纵向排序 0纵 1横 print(arr2) >>>> [[-0.5662314 -0.47501447 0.03701109] [-1.06994683 1.13578476 -0.26945096] [-1.09949419 -0.46383867 -0.34989365]]
[[-0.5662314 -0.47501447 0.03701109] [-1.06994683 -0.26945096 1.13578476] [-1.09949419 -0.46383867 -0.34989365]]
八:唯一化以及其他的集合逻辑
names =np.array(['bob','joe','will','bob','will','joe','joe']) print(np.unique(names)) #获取唯一化 # 成员资格 valuse =np.array([1,2,3,4,4,3,2,1]) print(np.in1d(valuse,[2,3,4])) >>>>> ['bob' 'joe' 'will'] [False True True True True True True False]

九:线性代数

x = np.array([[1,2],[3,4]]) y =np.array([[3,4],[1,2]]) print(x) print(y) print(np.dot(x,y)) #数组,内积,数组 >>>>> [[1 2] [3 4]] [[3 4] [1 2]] [[ 5 8] [13 20]]
from numpy.linalg import inv,qr X =np.arange(1,10).reshape(3,3) print(X) ni =inv(X) print(ni) mat =np.dot(X,ni) print(mat) >>>>> [[1 2 3] [4 5 6] [7 8 9]] [[-4.50359963e+15 9.00719925e+15 -4.50359963e+15] [ 9.00719925e+15 -1.80143985e+16 9.00719925e+15] [-4.50359963e+15 9.00719925e+15 -4.50359963e+15]] [[ 0. 0. 0.] [-4. 0. 4.] [ 0. 0. 8.]]


