NOIP模拟测试A2
好像是去年 8 月 1 日的模拟赛,主题采自南昌起义。
背景

A. 南
一道可爱的期望 DP。
一般来说,期望 DP 都是逆推,从最终状态往前推,这题也不例外。
这道题难度主要在于,第 \(k\) 次购买的价格为 \(k\),即价格与购买次数有关。
那我们就不能直接进行转移了,而是需要根据期望次数进行转移。
所以我们定义 \(f[i]\) 为已经获得 \(i\) 种武器,想要获得 \(n\) 种武器的期望次数。
初始状态 \(f[n] = 0\),即已经获得 \(n\) 种武器后想要取完 \(n\) 种武器的期望次数为 \(0\)。
\(f[i]\) 的转移还是很容易能想到的,分两种情况处理。
- 买到了已经有的类型,得到 \(f[i] = f[i] + 1\),已经获得的武器种类数保持不变,仍然为 \(i\)。
- 买到之前没有的类型,得到 \(f[i] = f[i+1]+1\),拥有的武器种类数增加了 \(1\)。
于是我们得到式子:
这个式子可以化简
定义 \(g[i]\) 为已经获得 \(i\) 种武器,想要获得 \(n\) 种武器的期望钱数。
同理,初始状态为 \(g[i] = 0\),仍然分取到已经有的和取到没有的两种情况处理。
每次加的钱数都是在上一次的基础上加了 \(1\),无论是买到已获得的还是未获得的。
这个式子仍然可以化简:
Code:
for(int i = n - 1;i >= 0; i--)
f[i] = f[i + 1] + (double)n / (double)(n - i);
for(int i = n - 1;i >= 0; i--)
g[i] = (double)i / (double)(n - i) * f[i] + g[i + 1] + f[i + 1] + (double)n / (double)(n - i);
B. 昌
要求根结点的最大值。
我们先假设根结点的最大值大于等于 \(x\),那么对于 \(\text{min}\) 操作来说,儿子的权值必须都大于等于 \(x\);对于 \(\text{max}\) 操作来说,儿子的权值至少要有一个大于等于 \(x\)。
依次类推,我们就可以找到这棵树有多少叶子结点的权值需要大于等于 \(x\),设这个值为 \(cnt\),那么 \(x\) 的最大值就是 \(k - cnt + 1\),\(k\) 为叶子个数。
所以我们可以求出来 \(cnt\),用它来求 \(x\)。
设 \(f[u]\) 为以 \(u\) 为根的子树内,至少有 \(f[u]\) 个叶子结点需要大于某个值。
对于叶子结点,有 \(f[u] = 1\)。
对于 \(\text{max}\) 操作:\(f[u] = \text{min}_{v \in son[u]}f[v]\)
对于 \(\text{min}\) 操作:\(f[u] = \Sigma_{v \in son[u]} f[v]\)
(对应的就是最开始那几句)
最终答案为 \(k - f[1] + 1\)。
Code:
void dfs(int x) {
if(e[x].empty()) {
dp[x] = 1;
return;
}
if(a[x] == 1) {
dp[x] = INT_MAX >> 1;
for(int i : e[x]) {
dfs(i);
dp[x] = min(dp[x],dp[i]);
}
} else {
dp[x] = 0;
for(int i : e[x]) {
dfs(i);
dp[x] += dp[i];
}
}
}
C. 起
不想写了,挂个官方题解


D. 义
好像是根号分治。
一个没听说过的东西,考后查了查,是一种思想,将要处理的整体分为前 \(\sqrt{n}\) 和剩余部分分别处理。
在这道题里十分的明显。
对于前 \(\sqrt{n}\) 种物品,每一种物品都有取完的可能。
但对于 \(\sqrt{n} + 1\) 到 \(n\) 种物品,如果把物品取完,就会超过背包容量,所以物品都取不完,相当于物品数量是无穷的。
所以我们可以分开进行 DP。
对于前 \(\sqrt{n}\) 种物品,定义 \(f[i][j]\) 为取完第 \(i\) 种物品,背包容量已经用 \(j\)。
有
假设有一条线段,表示我们背包的容量。
\(f[i-1][j]\) 表示不拿 \(i\) 物品,\(f[i][j-i]\) 表示再拿一个 \(i\) 物品,要减去多拿的方案数。
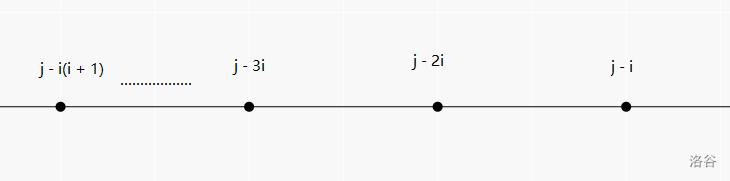
对于 \(f[i][j]\),是由 \(f[i][j - i]\) 转移而来的,\(f[i][j - i]\) 是由 \(f[i][j - 2i]\) 转移而来,但显然,不能拿 \(i(i+1)\) 个或以上,所以需要减去这部分。
再考虑剩下的部分,定义 \(g[i][j]\) 表示拿了 \(i\) 件 \(\sqrt{n} + 1\) 到 \(n\) 的物品,使用背包容量为 \(j\),有
表示每个物品都增加 \(1\) 的容量,变成下一种物品,就是不拿第 \(\sqrt{n} + 1\) 种物品
表示拿一个第 \(\sqrt{n} +1\) 种物品。
最后把两个数组的方案数相乘相加。
Code:
m = sqrt(n);
f[0][0] = f[1][0] = 1;
int k = 0;
for (int i = 1; i <= m; i++) {
k ^= 1;
for (int j = 1; j <= n; j++) {
f[k][j] = f[k ^ 1][j];
if (j >= i)
f[k][j] = (f[k][j] + f[k][j - i]) % MOD;
if (j >= i * (i + 1))
f[k][j] = (f[k][j] - f[k ^ 1][j - i * (i + 1)] + MOD) % MOD;
}
}
g[0][0] = 1;
for (int i = 0; i <= m; i++)
for (int j = 0; j <= n; j++) {
if (j + i <= n && i)
g[i][j + i] = (g[i][j + i] + g[i][j]) % MOD;
if (j + m + 1 <= n)
g[i + 1][j + m + 1] = (g[i + 1][j + m + 1] + g[i][j]) % MOD;
}
g[1][0] = 1;
for (int i = 0; i <= n; i++)
for (int j = 1; j <= m; j++)
ans = (ans + 1ll * f[k][i] * g[j][n - i] % MOD) % MOD;

 2023年6月12日模拟赛
2023年6月12日模拟赛
