CSP模拟25

炒币、凑数、同构、最近公共祖先

A. 炒币

举个栗子，对于序列

\[1,4,5 \]

在 \(1\) 处买进，在 \(5\) 处卖出是最优的选择。

为什么不选择在 \(4\) 处买，因为 \(4\) 处成本更高，所以我们可以把一段递增或递减的序列缩成几个互不相同的点。

例如

\[1,3,5,3,2,7 \]

变成

\[5,2,7 \]

只有这几个点是需要操作的。

若操作后的序列长度为偶数，直接输出；如果长度为奇数，不在第最后一个点把钱换成比特币。

#include <bits/stdc++.h>

using namespace std;

const int N = 500500;

int n;
long long a[N];

vector< pair<long long,int> > que;

bool vis[N];

int main() {
    scanf("%d",&n);

    for(int i = 1;i <= n; i++) {
        cin >> a[i];
    }

    bool flag = 0;

    if(a[1] > a[2]) {
        que.emplace_back(a[1],1);
        flag = 1;
    }

    for(int i = 2;i <= n; i++) {
        if((flag == 0 && a[i] >= a[i - 1]) && (a[i + 1] < a[i] || i == n)) {
            flag = 1;
            que.emplace_back(a[i],i);
        }
        else if((flag == 1 && a[i] <= a[i - 1]) && (a[i + 1] > a[i] || i == n)) {
            flag = 0;
            que.emplace_back(a[i],i);
        }
    }

    if(que.empty()) {
        for(int i = 1;i <= n; i++)
            cout << "0 ";
        return 0;
    }

    if(que.size() % 2 == 0) {
        for(auto const &it : que) {
            vis[it.second] = 1;
        }
        
        for(int i = 1;i <= n; i++)
            cout << vis[i] << " ";
        return 0;
    }
    else {
        if(que.size() == 1) {
            for(int i = 1;i <= n; i++) 
                cout << "0 ";
            
            return 0;
        }

        for(auto const &it : que) 
            vis[it.second] = 1;
        
        vis[que.back().second] = 0;

        for(int i = 1;i <= n; i++)
            cout << vis[i] << " ";

        return 0;
    }
    return 0;
}

B. 凑数

我们钦定 \(a\) 的性价比不低于 \(b\)，如果不满足就交换。

最多只能取 \(\left\lfloor \dfrac{n}{a} \right\rfloor\) 个 \(a\)，最多只能取 \(a-1\) 个 \(b\)。如果选 \(a\) 个 \(b\) 的话，我们完全可以用 \(b\) 个 \(a\) 来代替它，这样不是更优的，所以 \(b\) 最多取 \(a-1\) 个。

于是有策略：

1. 如果 \(a \leq \sqrt{n}\)，那么我们枚举 \(b\) 的数量；
2. 如果 \(a \geq \sqrt{n}\)，那么就有 \(\left\lfloor \frac{n}{a} \right\rfloor \leq \sqrt{n}\)，就枚举 \(a\) 的数量。

这两种方法枚举次数都不超过 \(\sqrt{n}\)，所以时间复杂度约为 \(\operatorname{O}(\sqrt{n})\)。

#include <bits/stdc++.h>

using namespace std;

int T;

long long n,a,b,x,y,z;

long long ans,tmp;

double val1,val2,val3;

void Work() {
    ans = LLONG_MAX;

    if(a * z < y * b) {
        swap(a,b);
        swap(y,z);
    }

    if(a * x <= y) {
        ans = n * x;
        return ;
    }

    if(b * x <= z) {
        ans = n / a * y + n % a * x;
        return ;
    }

    if(n / a < a - 1) {
        for(int i = 0;i <= (n / a); i++) {
            tmp = n - i * a;
            ans = min(ans,i * y + tmp / b * z + tmp % b * x);
        }
    }
    else {
        for(int i = 0;i <= a - 1; i++) {
            tmp = n - i * b;
            if(tmp >= 0)
                ans = min(ans,i * z + tmp / a * y + tmp % a * x);
        }
    }
    return ;
}

int main() {
#ifdef ONLINE_JUDGE == 1
    freopen("cs.in","r",stdin);
    freopen("cs.out","w",stdout);
#endif
    scanf("%d",&T);

    while(T--) {
        cin >> n >> a >> b >> x >> y >> z;
        
        Work();

        cout << ans << "\n";
    }

    fclose(stdin);
    fclose(stdout);
    return 0;
}

C. 同构

D. 最近公共祖先

考虑维护一个结点与其他所有被染色结点的权值最大的最近公共祖先权值，考虑线段树维护。

每次如何维护？

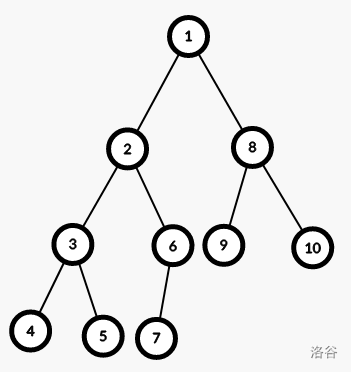
对于这棵树，我们要染色 \(3\) 号结点，我们需要维护的是它父亲结点的子树除了它之外的子树，而不去维护它自己的子树。

因为它自己子树中的点与染色的点的会被更外面的点维护，例如 \(10\) 号结点被染色的时候 \(4\) 号结点会被维护。

#include <bits/stdc++.h>

using namespace std;

const int N = 100500;

int n,m;

int val[N];

struct Edge{
    int next,to;
}e[N << 1];

int cnt,h[N];

void Add(int u,int v) {
    cnt ++;
    e[cnt].next = h[u];
    h[u] = cnt;
    e[cnt].to = v;

    return ;
}

int dfn[N],tot,fa[N];

int lim[N];
// 子树最大 dfn 

// Ready For Dfn
void dfs1(int x,int from) {
    fa[x] = from;
    tot ++;
    dfn[x] = tot;
    lim[x] = tot;

    for(int i = h[x];i; i = e[i].next) {
        int to = e[i].to;
        if(to == from)
            continue;
        
        dfs1(to,x);

        lim[x] = max(lim[x],lim[to]);
    }
}

// Segment Tree
int data[N];

#define lid id << 1
#define rid id << 1 | 1

class SegmentTree{
private:
    void Pushdown(int id) {
        data[lid] = max(data[lid],data[id]);
        data[rid] = max(data[rid],data[id]);
    }
public:
    void Update(int id,int l,int r,int L,int R,int k) {
        if(L <= l && r <= R) {
            data[id] = max(data[id],k);
            return ;
        }

        Pushdown(id);

        int mid = (l + r) >> 1;

        if(L <= mid) 
            Update(lid,l,mid,L,R,k);
        if(mid + 1 <= R)
            Update(rid,mid + 1,r,L,R,k);
    }

    int Query(int id,int l,int r,int pos) {
        if(l == r)
            return data[id];
        
        Pushdown(id);

        int mid = (l + r) >> 1;

        if(pos <= mid)
            return Query(lid,l,mid,pos);
        else
            return Query(rid,mid + 1,r,pos);
    }
}tree;

#undef lid
#undef rid

// Main
bool vis[N];

void Revise(int x,int from) {
    if(x == from)
        tree.Update(1,1,n,dfn[x],lim[x],val[x]);
    else {
        tree.Update(1,1,n,dfn[x],dfn[from] - 1,val[x]);

        if(lim[from] < lim[x])
            tree.Update(1,1,n,lim[from] + 1,lim[x],val[x]);
    }
}

void Modify(int x,int from) {
    Revise(x,from);

    if(vis[x])
        return ;
    vis[x] = 1;

    if(x == 1)
        return ;

    Modify(fa[x],x);
}

int main() {
    ios::sync_with_stdio(false);
    
    cin >> n >> m;
    for(int i = 1;i <= n; i++)
        cin >> val[i];
    
    for(int i = 1,u,v;i < n; i++) {
        cin >> u >> v;
        Add(u,v);
        Add(v,u);
    }

    dfs1(1,0);

    string str;
    int x;
    bool flag = 0;

    for(int i = 1;i <= m; i++) {
        cin >> str >> x;
        if(str == "Modify") {
            flag = 1;
            Modify(x,x);
        }
        else {
            if(!flag) {
                cout << "-1\n";
                continue;
            }

            cout << tree.Query(1,1,n,dfn[x]) << "\n";
        }
    }
    return 0;
}