CSP模拟24
yspm 专场 2。
原神派蒙、药水泡面、医生拍门、浴室泡沫
A. 原神派蒙
思路
结论:如果序列原先就合法,答案为 \(0\);否则,最多使用两个寄存器。
我们对 \(i \rightarrow a_i\) 建边得到若干个环,我们单独考虑一个环如何操作。
对于一个长度为 \(4\) 的数列,再包含两个寄存器,设两个寄存器的值分别为 \(x,y\)。
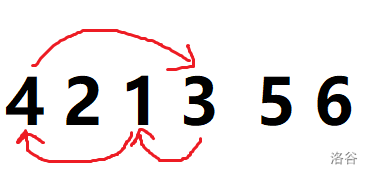
显然 \(4,1,3\) 组成了一个环,我们对其进行一些操作,使得他们回到他们想要到达的位置,即箭头指向的位置。
我们记 \(\operatorname{pos}_i\) 表示值 \(i\) 所在的位置,把 \(4\) 看作环的起点,那么把这个环拆成一条链就是 \(4,3,1\),下文称之为链。
首先我们将值 \(4\) 与值 \(5\) 交换位置,在此基础上再将值 \(3\) 与刚刚换到第五个位置的值 \(4\) 交换位置,除了链的最后一个元素外,剩下的元素按照上面的方式依次与第一个寄存器进行交换。
这样,我们链的第 \(1 \sim n-2\) 个元素都达到了自己的目标位置(他们指向的位置就是目标位置)。只剩下原本链的最后一个元素和倒数第二个元素没有达到目标位置。
我们寄存器原本的值 \(x\) 放在了链的第一个位置,链的倒数第二个元素放在了第一个寄存器的位置。链的最后一个元素仍在其原位置。
考虑如何处理剩下这两个元素。我们设链的倒数第二个值为 \(a\),最后一个值为 \(b\)。
我们考虑把值 \(b\) 与值 \(y\) 交换,现在 \(y\) 在链的末尾,\(b\) 在第二个寄存器;
再考虑把刚刚换到链的末尾的值 \(y\) 与第一个寄存器的值进行交换,即将值 \(y\) 与值 \(a\) 交换,现在 \(a\) 在链的末尾(达到了目标位置),\(y\) 在第一个寄存器;
再考虑将第二个寄存器的值与链首的值进行交换,即把 \(b\) 与 \(x\) 进行交换,\(b\) 达到了其目标位置。
到这里,前面的内存单元就已经合法了。我们再考虑一下两个寄存器顺序是否合法就可以了。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 100500;
int n,m;
int a[N];
vector< pair<int,int> > ans;
deque<int> st;
bool vis[N];
void dfs(int x) {
vis[x] = 1;
st.push_back(x);
if(!vis[a[x]])
dfs(a[x]);
return ;
}
int main() {
ios::sync_with_stdio(false);
cin >> n;
for(int i = 1;i <= n; i++)
cin >> a[i];
a[n + 1] = n + 1;
a[n + 2] = n + 2;
for(int i = 1;i <= n; i++) {
if(!vis[i] && i != a[i]) {
st.clear();
dfs(i);
m = 2;
for(auto const &it : st) {
if(it == st.back())
break;
ans.emplace_back(it,n + 1);
swap(a[it],a[n + 1]);
}
ans.emplace_back(st.back(),n + 2);
swap(a[st.back()],a[n + 2]);
ans.emplace_back(st.back(),n + 1);
swap(a[st.back()],a[n + 1]);
ans.emplace_back(st.front(),n + 2);
swap(a[st.front()],a[n + 2]);
}
}
if(a[n + 1] != n + 1)
ans.emplace_back(n + 1,n + 2);
cout << m << " " << ans.size() << "\n";
for(auto const &it : ans)
cout << it.first << " " << it.second << "\n";
return 0;
}
B. 药水泡面
基本与CF280C相同。
选中了一个点,这个点就被删除了,即一个点只能被选一次。一棵树被删除等同于每个点都被选中,所以可以这么转化。
想要选中这个要被删除的点,不能让它由于它子树中的点被删除,在此条件下,该结点要被删除,所以为 \(\dfrac{1}{\operatorname{size}_x}\)。
所以最终答案为
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 2005000;
const int Mod = 998244353;
int n;
struct Edge{
int next,to;
}e[N << 1];
int cnt,h[N];
void Add(int u,int v) {
cnt ++;
e[cnt].next = h[u];
h[u] = cnt;
e[cnt].to = v;
return ;
}
long long Pow(long long a ,long long b) {
long long res = 1 ;
long long base = a % Mod;
while(b) {
if(b & 1)
res = (res * base) % Mod;
base = (base * base) % Mod;
b >>= 1;
}
return res;
}
long long Inv(long long x) {
return Pow(x % Mod,Mod - 2) % Mod;
}
int size[N];
void dfs(int x,int fa) {
size[x] = 1;
for(int i = h[x];i;i = e[i].next) {
int to = e[i].to;
if(to == fa)
continue;
dfs(to,x);
size[x] += size[to];
}
}
int main() {
ios::sync_with_stdio(false);
cin >> n;
for(int i = 1,u,v;i < n; i++) {
cin >> u >> v;
Add(u,v);
Add(v,u);
}
dfs(1,0);
long long ans = 0;
for(int i = 1;i <= n; i++)
ans = (ans + 1ll * Inv(size[i]) % Mod) % Mod;
cout << ans << "\n";
return 0;
}


