CSP模拟20
跳火山、赞美太阳、幽邃主教群、整理
A. [POI2014] PAN-Solar Panels
区间 \(\left( l,r \right]\) 中存在 \(n\) 的倍数的充要条件是 \(\left\lfloor \frac{r}{n}\right\rfloor > \left\lfloor \frac{l}{n}\right\rfloor\)。
证明:记有整数 \(k\) 满足 \(k \times n \in \left( l,r \right]\)。
那么有 $$\displaystyle l < k \times n \leqslant r \Longleftrightarrow \dfrac{l}{n} < k \leqslant \dfrac{r}{n} \Longleftrightarrow \left\lfloor \frac{l}{n}\right\rfloor < \left\lfloor \frac{r}{n}\right\rfloor$$
证毕。
记 \(\gcd(x,y)=k\),我们可以枚举 \(k\),因为 \(a \leqslant x \leqslant b\),所以我们可以枚举 \(k\)。
但暴力枚举 \(k\) 肯定是会超时,那我们就用整除分块优化。
Code
#include <bits/stdc++.h>
using namespace std;
int n;
int a,b,c,d;
int last,ans;
int main() {
#ifdef ONLINE_JUDGE == 1
freopen("melina.in","r",stdin);
freopen("melina.out","w",stdout);
#endif
cin >> n;
for(int t = 1;t <= n; t++) {
cin >> a >> b >> c >> d;
for(int i = 1;i <= b && i <= d; i = last + 1) {
last = min(d / (d / i),b / (b / i));
// 整除分块的右端点,实际是范围内的最大值
if(b / last > (a - 1) / last && d / last > (c - 1) / last)
ans = last;// 利用性质
}
cout << ans << "\n";
}
#ifdef ONLINE_JUDGE == 1
fclose(stdin);
fclose(stdout);
#endif
return 0;
}
B. [POI2010] CHO-Hamsters]
在 AC 自动机上跑 DP,再矩阵快速幂优化。
直接咕!
C. 「JOISC 2016 Day 2」雇佣计划
假设我们有一条线从下向上移动,可以理解为 \(b_i\) 的递增。
在这个过程中,会有数小于 \(b_i\),导致答案数发生变化。我们将小于 \(b_i\) 的数称作不存在。
如下图:
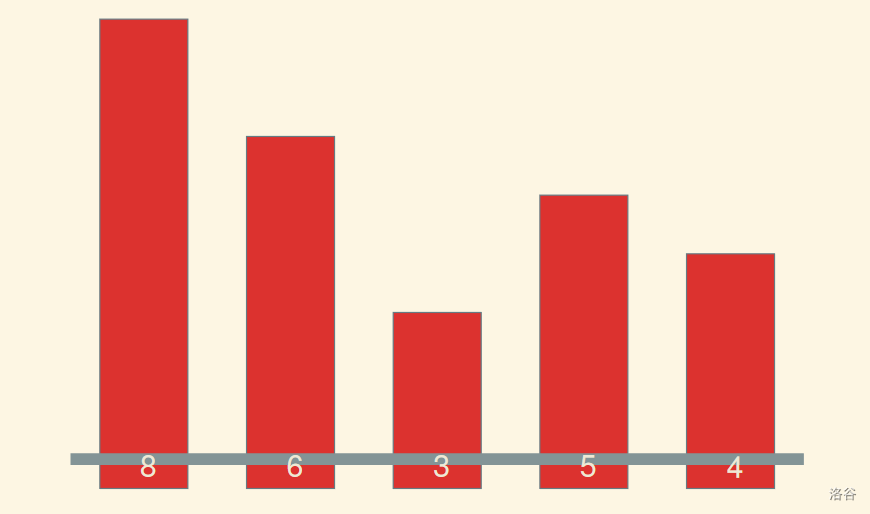
以下的过程不是互相独立的。
如果 \(b_i>3\),由于 \(3\) 的两边都是存在的,答案数会加 \(1\);
如果 \(b_i>4\),由于 \(4\) 的左边存在,右边不存在,所以答案数不变;
如果 \(b_i>5\),由于 \(5\) 的两边都不存在,答案数会减 \(1\)。
以上是 \(40 \text{pts}\) 的思路,对正解有一定的启发。
不去考虑连通块的问题,而是去考虑数与数之间的空。
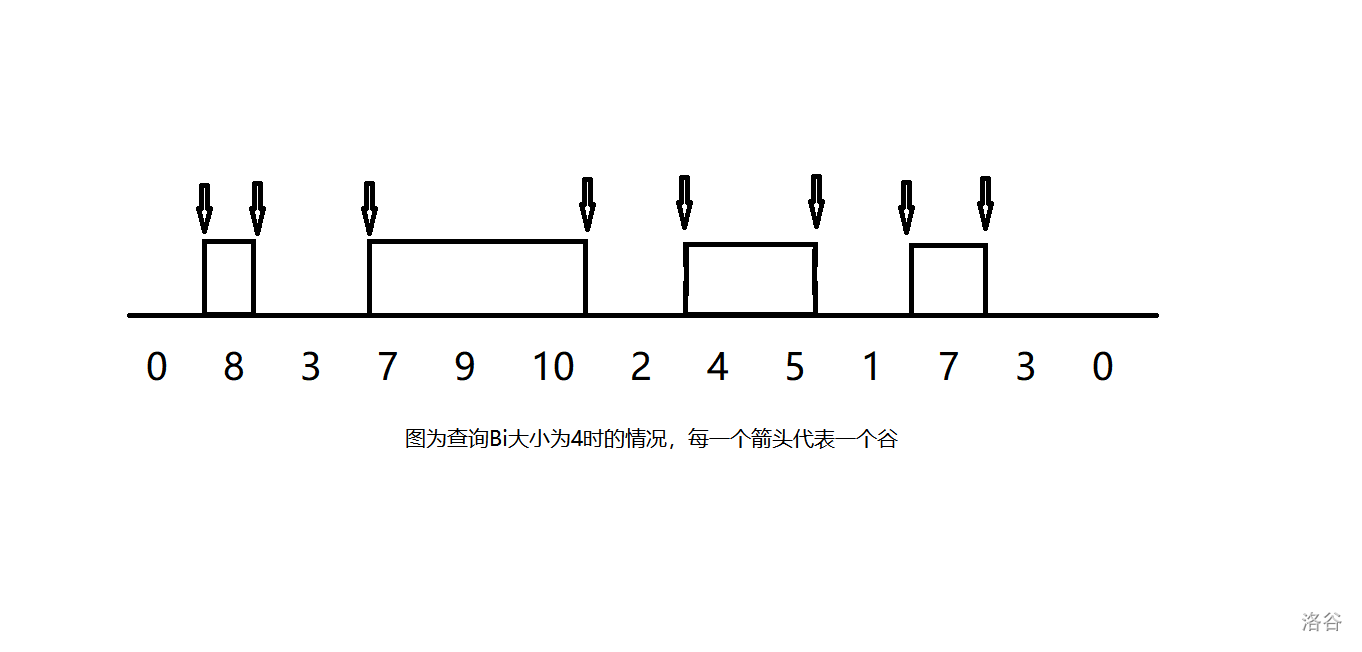
每两个整数之间就可能称为一个谷,显然,一个连通块可以产生两个谷,那么最终答案就是谷的数量除以 \(2\)。
我们需要维护有多少个空能够满足成为谷的条件。
考虑和上面 \(40 \text{pts}\) 做法的共通之处,不过也不太一样。什么样的空格可以成为谷?什么样的情况可以对答案产生贡献。
显然,谷的一边的数要小于 \(b_i\),另一边的数要大于等于 \(b_i\),形式化地,我们有:
那我们用什么维护呢?需要在 \(\operatorname{O}(\log n)\) 复杂度内维护上述条件点的数量,还要支持单点修改区间查询,显然,用我们树状数组。
把询问条件差分用树状数组维护,记得离散化。
还有就是 \(0\) 和 \(n+1\) 这两个点,要记录最两边的谷。
#include <bits/stdc++.h>
using namespace std;
const int N = 1005000;
int n,m;
int val[N];
int len,b[N];
int tot = 0;
struct Query{
int opt;
int x,y;
}q[N];
int Get(int x) {
return lower_bound(b + 1,b + len + 1,x) - b;
}
class BIT{
private:
int sum[N];
int lowbit(int x) {
return x & (-x);
}
public:
void Update(int x,int y) {
for(int i = x;i <= 3 * n; i += lowbit(i))
sum[i] += y;
}
int Query(int x) {
int ans = 0;
for(int i = x;i;i -= lowbit(i))
ans += sum[i];
return ans;
}
}tree;
void Add(int x,int y) {
int l = val[x - 1],r = val[x];
if(l > r)
swap(l,r);
tree.Update(++l,y);
tree.Update(r + 1,-y);
l = val[x];
r = val[x + 1];
if(l > r)
swap(l,r);
tree.Update(++l,y);
tree.Update(r + 1,-y);
}
int main() {
#ifdef ONLINE_JUDGE == 1
freopen("darkteam.in","r",stdin);
freopen("darkteam.out","w",stdout);
#endif
cin >> n >> m;
for(int i = 1;i <= n; i++)
cin >> val[i];
for(int i = 1;i <= m; i++) {
cin >> q[i].opt;
if(q[i].opt == 1)
cin >> q[i].x;
else
cin >> q[i].x >> q[i].y;
}
for(int i = 1;i <= n; i++) {
tot ++;
b[tot] = val[i];
}
for(int i = 1;i <= m; i++) {
tot ++;
if(q[i].opt == 1)
b[tot] = q[i].x;
else
b[tot] = q[i].y;
}
sort(b + 1,b + tot + 1);
len = unique(b + 1,b + tot + 1) - (b + 1);
for(int i = 1;i <= n; i++)
val[i] = Get(val[i]);
for(int i = 1;i <= m; i++) {
if(q[i].opt == 1)
q[i].x = Get(q[i].x);
else
q[i].y = Get(q[i].y);
}
for(int i = 1;i <= n + 1; i++) {
int l = val[i - 1],r = val[i];
if(l > r)
swap(l,r);
tree.Update(++l,1);
tree.Update(++r,-1);
}
for(int i = 1;i <= m; i++) {
if(q[i].opt == 1)
cout << tree.Query(q[i].x) / 2 << "\n";
else {
Add(q[i].x,-1);
val[q[i].x] = q[i].y;
Add(q[i].x,1);
}
}
#ifdef ONLINE_JUDGE == 1
fclose(stdin);
fclose(stdout);
#endif
return 0;
}
D. [ABC134F] Permutation Oddness
题目大意
定义一个 \(1 \sim n\) 的排列 \(p\) 的「怪异度」为
求「怪异度」为 \(m\) 的 \(1 \sim n\) 的排列数,答案对 \(10^9+7\) 取模。
思路
考虑把 \(p_i\) 和 \(i\) 看作小球与盒子,方便题意理解。
考虑球与盒子的匹配。
假设球在左侧,盒子在右侧,他们构成了一个二分图。
从上到下顺着排列每组球与盒子,球与盒子之间有一条横线。
我们发现,假设第 \(i\) 个盒子与 \(j\) 个球相连,他们之间的距离为 \(\left\lvert i - j \right\rvert\),他们产生的贡献相当于从 \(i\) 到 \(j\) 的连线穿过的横线的数量。
那么我们考虑状态如何设计,记 \(dp_{i,j,k}\) 表示已经匹配了前 \(i\) 行,有 \(j\) 组球与盒子未匹配,怪异度为 \(k\) 的方案数。
那么初始值为 \(dp_{0,0,0}=1\),答案为 \(dp_{n,0,m}\) 表示匹配了前 \(i\) 行,没有球与盒子未匹配,怪异度为 \(m\) 的方案数。
考虑转移,对于一行,有一个球和一个盒子,可以匹配 \(0,1,2\) 组三种可能,那么就分这三种情况进行转移。
匹配 \(0\) 组
都不匹配的话,应该是 \(dp_{i-1,j-1,k-2j}\)。
考虑第二维为什么是从 \(j-1\) 个未匹配组转移过来。
先考虑我们匹配 \(1\) 组的情况,我们新加入了 \(1\) 组,即第 \(i\) 行的球与盒子,又匹配了 \(1\) 组,那么新的没有匹配的组数没有发生变化,即第二维从 \(j\) 转移到 \(j\)。
那么匹配 \(2\) 组的情况,相比于匹配 \(1\) 组的情况多匹配了一组,所以要从 \(j + 1\) 转移到 \(j\);同理,匹配 \(0\) 组的情况就要从 \(j-1\) 转移到 \(j\)。
再考虑第三维。原本前面那些没有被匹配的盒子与球是可能被匹配到第 \(i\) 行及以后的,但是现在我们考虑的转移第 \(i\) 行并没有匹配这 \(j\) 组盒子与球。
那么这 \(j\) 组盒子与球只能匹配到第 \(i +1\) 行及以后,那么相等于我们前面的 \(j\) 组球与盒子又需要多穿过一条横线,那么总共 \(2j\) 个物品,就使得怪异值增加了 \(2j\),所以从 \(k-2j\) 转移过来。
匹配 \(1\) 组
将第 \(i\) 个球与前面的 \(i-1\) 行未被匹配的 \(j\) 个盒子进行匹配,有 \(j\) 种选择,每种选择的方案数为 \(j \times dp_{i-1,j,k-2j}\)。
用第 \(i\) 个盒子去匹配球的方案数同理。
第 \(i\) 个球连第 \(i\) 个盒子的方案数单独处理,为 \(dp_{i-1,j,k-2j}\)。
匹配 \(2\) 组
如果要匹配两组,那么第 \(i\) 行的球与盒子之间不能相互选择。
第 \(i\) 行的球与前 \(i-1\) 行的 \(j+1\) 个未匹配的盒子转移过来,盒子同理,根据乘法原理,有 \((j + 1)^2dp_{i-1,j+1,k-2j}\) 种方案。
状态转移方程
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long MainType;
const int N = 55;
const int Mod = 1e9 + 7;
int n,m;
MainType dp[N][N][N * N];
// dp[i][j][k]
// 对于前 i 组有 j 组没有配对,怪异度为 k 的方案数
int main() {
#ifdef ONLINE_JUDGE == 1
freopen("genshin.in","r",stdin);
freopen("genshin.out","w",stdout);
#endif
cin >> n >> m;
dp[0][0][0] = 1;
for(int i = 1;i <= n; i++) {
for(int j = 0;j <= i; j++) {
for(int k = j * 2;k <= m; k++) {
if(j < 1)
dp[i][j][k] = (dp[i - 1][j + 1][k - j * 2] * (j + 1) % Mod * (j + 1) % Mod + dp[i - 1][j][k - j * 2] * (j * 2 + 1) % Mod) % Mod;
else
dp[i][j][k] = (dp[i - 1][j + 1][k - j * 2] * (j + 1) % Mod * (j + 1) % Mod + dp[i - 1][j][k - j * 2] * (j * 2 + 1) % Mod + dp[i - 1][j - 1][k - j * 2] % Mod) % Mod;
}
}
}
cout << dp[n][0][m] % Mod;
#ifdef ONLINE_JUDGE == 1
fclose(stdin);
fclose(stdout);
#endif
return 0;
}

