CF1060E Sergey and Subway

题目大意

给定一棵树，每两个有边直接相连的点之间距离为 \(1\)。现在我们要给所有原来距离为 \(2\) 的城市之间修一条长度为 \(1\) 的道路。

记 \(\operatorname{dis}(a,b)\) 表示 \(a,b\) 之间的最短距离，求

\[\sum_{i=1}^n\sum^{n}_{j=i+1}\operatorname{dis}(i,j) \]

思路

考虑修改后的树任意两点间距离与修改前的关系。

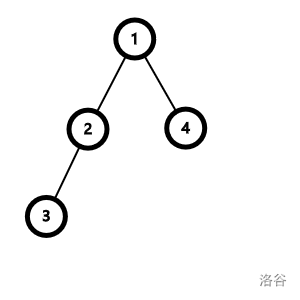
例如，\(1\) 和 \(3\) 原本距离为 \(2\)，现在距离为 \(1\)；\(3\) 和 \(4\) 原本距离为 \(3\)，现在距离为 \(2\)。

我们发现，对于原树中两点间的距离 \(\operatorname{dis}\)，现在的距离为 \(\lfloor \frac{dis + 1}{2} \rfloor\)。

考虑把这个式子转化一下，变成

\[\left\lfloor \frac{dis + 1}{2} \right\rfloor=\dfrac{\operatorname{dis}+\left[ \operatorname{dis}\equiv1(\!\!\!\!\mod 2 ) \right]}{2} \]

那么我们代入题目给出的式子，得到

\[\sum^{n}_{i=1}\sum^{n}_{j=i+1}(\dfrac{\operatorname{dis}(i,j)+\left[ \operatorname{dis}(i,j)\equiv1(\!\!\!\!\mod 2 ) \right]}{2}) \]

很显然，我们发现，最终答案与边权的奇偶性和原树边权和有关。

考虑如何求路径长度？两点间距离为

\[\operatorname{dis}(i,j)=\operatorname{dep}_i+\operatorname{dep}_j-2\times \operatorname{dep_{\operatorname{lca}(i,j)}} \]

其中后面 \(-2\times \operatorname{dep_{\operatorname{lca}(i,j)}}\) 的部分与路径长度的奇偶性无关，那么直接统计 \(\operatorname{dep}_i\) 和 \(\operatorname{dep}_j\) 奇偶性不同的点对数量就可以求出路径长度为奇数的路径数量。

Code

#include <bits/stdc++.h>

using namespace std;

const int N = 200500;

int n;

struct Edge{
    int next,to;
}e[N << 1];

int h[N],cnt;

void Add(int u,int v) {
    cnt ++;
    e[cnt].next = h[u];
    h[u] = cnt;
    e[cnt].to = v;
}

namespace SOL{
    long long ans = 0;
    int size[N],cnt[N];

    void dfs(int x,int fa,int dep) {
        cnt[dep ^ 1] ++;
        size[x] = 1;

        for(int i = h[x];i;i = e[i].next) {
            int to = e[i].to;

            if(to == fa) 
                continue;
            
            dfs(to,x,dep ^ 1);
            size[x] += size[to];
        }

        ans += 1ll * (n - size[x]) * size[x];
    }
    
    void Work() {
        memset(cnt,0,sizeof(cnt));
        memset(size,0,sizeof(size));

        dfs(1,1,0);

        ans = ans + 1ll * cnt[0] * cnt[1];
        ans /= 2;

        cout << ans << "\n";
        return ;
    }
}

int main() {
#ifdef ONLINE_JUDGE == 1
    freopen("road.in","r",stdin);
    freopen("road.out","w",stdout);
#endif
    scanf("%d",&n);

    for(int i = 1,u,v;i < n; i++) {
        scanf("%d%d",&u,&v);
        Add(u,v);
        Add(v,u);
    }

    SOL::Work();

    fclose(stdin);
    fclose(stdout);
    return 0;
}