位运算学习笔记

\(\text{Tips}:\) 除特殊说明外，本篇博客二进制数最低位默认为第 \(0\) 位。

二进制数

• 有符号数和无符号数
  二进制数的最高位是符号位，正数符号位为 \(0\)，负数符号位为 \(1\)。
• 原码、补码和反码

原码：原码就是机器数，是加了一位符号位的二进制数。

反码：原码在乘除运算时没有问题，但在加减运算时会出错。
用原码来运算 \(1 + (-1) = -2\)，所以我们发明反码，正数的反码就是它本身，负数的反码将原码除符号位外的各位取反（\(1\) 变 \(0\)，\(0\) 变 \(1\)）。

补码：在反码中，\(0\) 有了 \(0\) 和 \(-0\) 两种形态。
坏了啊，这怎么办？
所以发明补码，正数的补码仍然是其本身，负数的补码在其原码基础上，除符号位不变，其他各位取反，最后值再加 \(1\)。

注：

1. 正数的原码、反码和补码相同。

2. 负数的补码 \(=\) 其反码 \(+1\)。

3. \(0\) 的补码、反码都是 \(0\)。

4. 计算机以补码形式运算。

位运算

1. 基础位运算

• & 按位与

  两个相应的二进制位都为 \(1\) 则为 \(1\)，否则为 \(0\)。

• | 按位或

  两个相应的二进制位只要有一个为 \(1\) 就为 \(1\)，否则为 \(0\)。

• ^ 按位异或

  两个相应的二进制位相同则为 \(0\)，不同为 \(1\)，也可理解为不进位的二进制加法。

• ~ 按位取反

  将一个二进制数的 \(1\) 变成 \(0\)，\(0\) 变成 \(1\)。

• << 或 >> 移位运算

  二进制下将数字向左或右移动，原本位置用 \(0\) 补充。
  \(1<<n = 2^n\) \(n<<1 = 2n\)
  注：算术右移的结果向下取整。

• \(\text{lowbit}\) 运算：即 x&(-x)。

  得到 \(x\) 的二进制数从最低位起到第一个 \(1\) 的位置的二进制数的值。

  例如，\(114514\) 的二进制数是 \((1 1011 1111 0101 0010)_2\)，它从最低位起第一个 \(1\) 在第 \(1\) 位，因此进行 \(\text{lowbit}\) 运算后得到的值为 \(2^1\)，即 \(2\)。

2. 运算符优先级

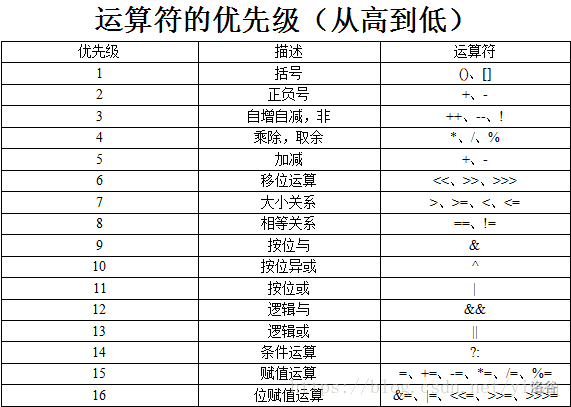
记这么多优先级肯定是不合常理的，建议多写一些括号就好。

3. 二进制状态压缩

二进制状态压缩，是指将一个长度为 \(m\) 的 \(\text{bool}\) 数组用一个 \(m\) 位二进制整数表示并存储的方法。
可以利用下列位运算操作实现原 \(\text{bool}\) 数组中对应下标元素的存取。

// 取出整数 n 在二进制表示下的第 k 位
	(n >> k) & 1

// 取出整数 n 在二进制表示下的第 0 ~ k - 1 位 (后 k 位)
	n & ((1 << k) - 1)

// 把整数 n 在二进制表示下的第 k 位 取反
	n ^ (1 << k)

// 对整数 n 在二进制表示下的第 k 位赋值 1
	n | (1 << k)

// 对整数 n 在二进制表示下的第 k 位赋值 0
	n & (~(1 << k))

此部分参考自李煜东《算法竞赛进阶指南》。