Codeforces Round #619 (Div. 2)
QAQ:
A. Three Strings
题意:
给你三个等长字符串a,b,c,你对于每一位i,你必须要cI去替换ai或者bi,问最后能不能让a串和b串相同。
思路:
简单题,直接模拟即可,详细见代码。
代码:
#include<bits/stdc++.h> using namespace std; string a,b,c; void solve() { cin >> a>>b>>c; int len = a.size(); for(int i = 0;i<len;++i) { if((a[i]==c[i]||c[i]==b[i])) continue; else { cout << "NO\n"; return ; } } cout << "YES\n"; return ; } int main() { int T; cin >> T; while(T--) { solve(); } return 0; }
B. Motarack's Birthday
题意:
给你一个数组,但有些数已经缺失了(用-1表示),你打算把缺失的值用k代替,求一个何时的k使得填完之后,相邻两数之差的绝对值最小。输出k,以及最大的差绝对值。
思路:
考虑k所能对总的结果所能产生影响的实际上只有一段连续的-1的左右两个点的值与k的差值的绝对值,根据这个思路那我们k的值应该是所有端点中最大的和最小的之间的中间值。细节请见代码。
代码:
#include<bits/stdc++.h> using namespace std; typedef long long LL; const int maxn = 1e5+100; LL num[maxn]; vector<int>vec; void solve() { int n; scanf("%d",&n); vec.clear(); for(int i = 1;i<=n;++i) cin >>num[i]; for(int i = 1;i<=n;++i) { if(num[i]!=-1) { if(i-1>0&&num[i-1]==-1) vec.push_back(num[i]); else if(i+1<=n&&num[i+1]==-1) vec.push_back(num[i]); } } if(vec.size()==0) { cout << "0 0\n"; return; } sort(vec.begin(),vec.end()); LL k =(vec[0]+vec[vec.size()-1])/2; for(int i = 1;i<=n;++i) { if(num[i]==-1) num[i] = k; } LL ma = abs(num[1]-num[2]); for(int i = 2;i<n;++i) ma = max(ma,abs(num[i]-num[i+1])); cout << ma << " " << k << "\n"; return ; } int main() { int T; cin >> T; while(T--) { solve(); } return 0; }
C. Ayoub's function
题意:
对于一个01字符串s,定义一个函数f(s),等满足条件的(l,r)的对数,(1<=l<=r<=len(s)),条件为sl到sr至少有一个字符“1”。现在给你两个数n和m,代表字符串s的长度以及字符串中1的数目,求最大的f(s)。
思路:
设字符串中0的数目位k,k = n-m,分类讨论(r-l=0的符合条件的对数已经确定,我们只讨论r-l>0的情况)
如果k<=m+1,则我们总能构造出一个字符串,此时字符串任意r-l>0的l,r都符合条件,所以此时的答案为C(n,2)+m(长度为1符合情况的字串数)
如果k>m+1,则我们现在相当于用m个1去分割长度为k的0串,使其成为m+1个段,那么不合法的方案应该是sum{ C(len(第i个段的长度),2),1<=i<=m+1},经过计算,我们发现最小的情况应该是每一段的长度尽可能接近时的值,所以按照这个思路去求值即可。详细可见代码
代码:
#include<bits/stdc++.h> using namespace std; typedef long long LL; void solve() { LL n,m; cin >> n >> m; if(n-m<=m+1) { cout << (n*(n-1))/2+n-(n-m) << "\n"; } else { if(m==0) { cout << "0\n"; return ; } LL num0 = n-m; LL d = num0/(m+1),d1 = num0 - d*(m+1); LL ans = 0; LL k = m; ans+=(d1*((d+1)*(d)/2)); k-=d1; ans+=((k+1)*(d*(d-1)/2)); cout << (n*(n-1))/2-ans+m <<"\n"; //cout << (n*(n-1))/2+n-m-((n-2*m)*(n-2*m-1)/2+(n-2*m)) << "\n"; } return ; } int main() { int T; cin >> T; while(T--) { solve(); } return 0; }
D. Time to Run
题意:
给你一个n*m的矩阵,矩阵中每两个相邻的格子都有两条方向相反的路径,问你能否构造出一个长度k的路径(每条道路只能经过一次)。能输出YES以及路径,否则输出NO。例如当n = 3以及m = 4,矩阵如下
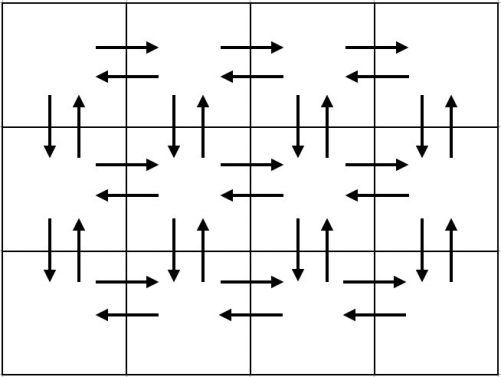
思路:
构造题,我们需要构造一条能够遍历每条道路的路径(这是这个图所能实现的最长路径),构造方案如下,需要特判下n = 1以及m = 1的情况。

红色为横向,蓝色为纵向。具体细节可以见代码。
代码:
#include <bits/stdc++.h> using namespace std; typedef long long LL; struct Node { int num; char c; Node(){}; Node(int _num,char _c):num(_num),c(_c){} }; vector<Node> ans; void solve() { // string ans; LL n,m,k; cin >> n >> m >>k; if(n==1) { ans.push_back(Node(m-1,'R')); ans.push_back(Node(m-1,'L')); } else if(m==1) { ans.push_back(Node(n-1,'D')); ans.push_back(Node(n-1,'U')); } else { for(int i = 1;i<n;++i) { ans.push_back(Node(m-1,'R')); ans.push_back(Node(m-1,'L')); ans.push_back(Node(1,'D')); } ans.push_back(Node(m-1,'R')); for(int i = 1;i<m;++i) { ans.push_back(Node(n-1,'U')); ans.push_back(Node(n-1,'D')); ans.push_back(Node(1,'L')); } ans.push_back(Node(n-1,'U')); } if(k>(4*m*n-2*m-2*n)) printf("NO\n"); else { queue<Node>q; printf("YES\n"); int l = 0; while(k>0) { int p = min(k,(LL)ans[l].num); // cout << p << " " << ans[l].c << "\n"; q.push(Node(p,ans[l].c)); k-=p; ++l; } cout << q.size() << "\n"; while(!q.empty()) { Node tmp = q.front(); cout << tmp.num << " " << tmp.c << "\n"; q.pop(); } } return ; } int main() { solve(); return 0; }

