lucas定理

Update:

代码已更新，之前的代码算数时会溢出 QAQ

应用：

Lucas定理的应用范围在于大的组合数取模。简而言之，就是用来求 c(n,m) mod p，p为素数的值。

定义：

C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p

求解上式时，递归出口为 m = 0 时返回 1.

证明：

下面附上Lucas定理的一种证明，见下图，参考冯志刚《初等数论》第37页。

 

 对于证明过程的一些解释：

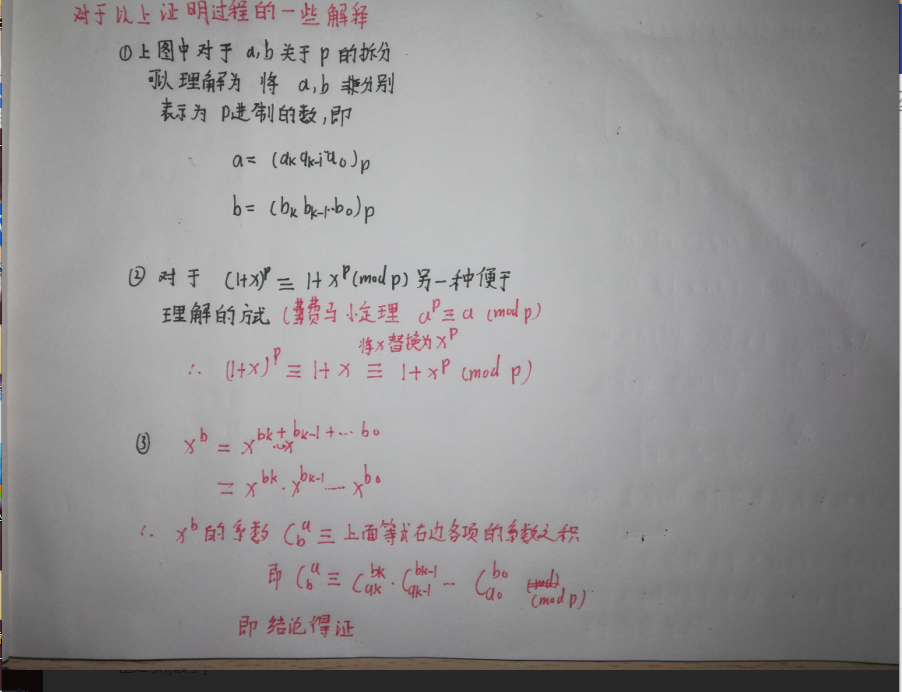
update：上面第三条的C(a,b)应该是C(b,a)。

代码实现：

typedef long long LL;
const LL mod = 1e9+7;
LL quick_pow(LL x, LL n, LL p)// 快速幂求x^n mod p 的结果
{
    if(n==0)
        return 1;
    if(n==1)
        return x%p;
    LL ans = 1;
    LL tmp = x%p;
    while(n)
    {
        if(n&1)
        {
            ans = (ans*tmp)%p;
        }
        tmp = tmp*tmp%p;
        n>>=1;
    }
    return ans%p;
}
LL inv(LL b,LL p) //求数 b mod p 的逆元
{
    return quick_pow(b,p-2,p);
}
LL C(LL n,LL m,LL p)//组合数取模
{
    if(m==0|| m== n)
        return 1;
    if(m==1||m==n-1)
        return n%p;
        m = min(m,n-m);
    LL up = 1,down = 1;
    for(LL i = n-m+1;i<=n;i++)
        up=(up*i)%p;
    for(LL i = 1;i<=m;i++)
        down=(down*i)%p;
    up%=p;
    down%=p;
    return (up*(inv(down,p)%p))%p;
}
LL lucas(LL n,LL m,LL p)//递归lucas函数
{
    if(m==0)
        return 1;
    return lucas(n/p,m/p,p)*C(n%p,m%p,p)%p;
}

如果对求逆元不是十分了解，欢迎去我的上一篇博客去看看。

如果还有疑问，欢迎在评论区留言/