归并排序和快速排序的衍生问题

分治算法思想

　　前两节的归并排序和快速排序都使用了分治算法的排序思想，分治算法：顾名思义，分而治之，就是将原问题分割成同等结构的子问题，之后将子问题逐一解决后，原问题也就得到了解决。

以下使用分支算法的思想解决一些问题。

 

逆数对

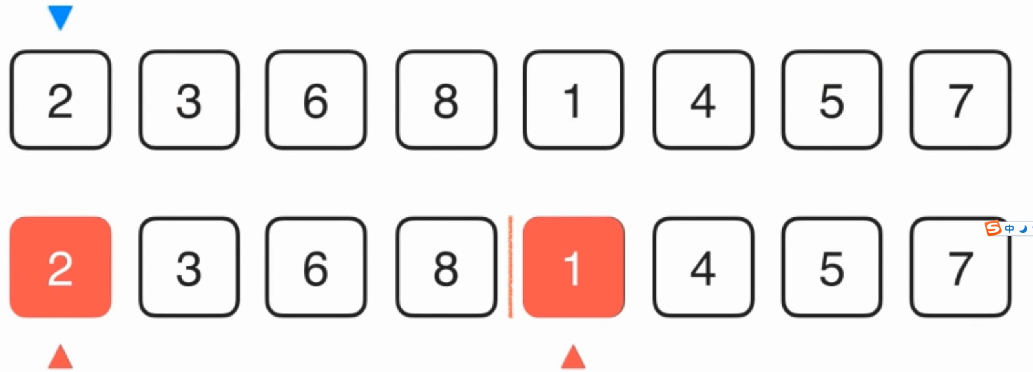
　　计算数组中逆数对的个数，一个数组中逆数对的个数能表示数组的有序程度。如下图所示‘2’和‘1’便是一对逆数对。

使用归并排序求逆数对

　　在归并排序中对两部分数据进行合并时，可以计算出某一个数据的逆数对，如上图所示，在合并两部分数据时，首先1和2比较，1小于2，因为两部分数据都是从小到大排序的，所以1同时也会与2后边的数据构成逆数对，依次类推，进行合并后续的数据时，可以分别计算出构成的逆数对，所有逆数对之和便是此数组的逆数对。

　　如下给出代码示例，代码基本与归并排序算法保持一致，只是在合并时记录了逆数对的个数。

// 对于一个大小为N的数组, 其最大的逆序数对个数为 N*(N-1)/2, 非常容易产生整型溢出
// merge函数求出在arr[l...mid]和arr[mid+1...r]有序的基础上, arr[l...r]的逆序数对个数
long long __merge( int arr[], int l, int mid, int r)
{
    int *aux = new int[r-l+1];
    for( int i = l ; i <= r ; i ++ )
        aux[i-l] = arr[i];

    // 初始化逆序数对个数 res = 0
    long long res = 0;
    // 初始化，i指向左半部分的起始索引位置l；j指向右半部分起始索引位置mid+1
    int j = l, k = mid + 1;
    for( int i = l ; i <= r ; i ++ ){
        if( j > mid ){ // 如果左半部分元素已经全部处理完毕
            arr[i] = aux[k-l];
            k ++;
        }
        else if( k > r ){ // 如果右半部分元素已经全部处理完毕
            arr[i] = aux[j-l];
            j ++;
        }
        else if( aux[j-l] <= aux[k-l] ){ // 左半部分所指元素 <= 右半部分所指元素
            arr[i] = aux[j-l];
            j ++;
        }
        else{ // 右半部分所指元素 < 左半部分所指元素
            arr[i] = aux[k-l];
            k ++;
            // 此时, 因为右半部分k所指的元素小
            // 这个元素和左半部分的所有未处理的元素都构成了逆序数对
            // 左半部分此时未处理的元素个数为 mid - j + 1
            res += (long long)(mid - j + 1);
        }
    }
    delete[] aux;
    return res;
}

// 求arr[l..r]范围的逆序数对个数
// 思考: 归并排序的优化可否用于求逆序数对的算法? :)
long long __inversionCount(int arr[], int l, int r)
{
    if( l >= r )
        return 0;

    int mid = l + (r-l)/2;

    // 求出 arr[l...mid] 范围的逆序数
    long long res1 = __inversionCount( arr, l, mid);
    // 求出 arr[mid+1...r] 范围的逆序数
    long long res2 = __inversionCount( arr, mid+1, r);

    return res1 + res2 + __merge( arr, l, mid, r);
}

// 递归求arr的逆序数对个数
long long inversionCount(int arr[], int n)
{
    return __inversionCount(arr, 0, n-1);
}

　　

取数组中第N大的元素

　　取出一个数组中第N大的元素，可以通过快速排序实现此需求。

使用快速排序取第N大的元素

// partition 过程, 和快排的partition一样
// 思考: 双路快排和三路快排的思想能不能用在selection算法中? :)
template <typename T>
int __partition( T arr[], int l, int r )
{
    int p = rand()%(r-l+1) + l;
    swap( arr[l] , arr[p] );

    int j = l; //[l+1...j] < p ; [lt+1..i) > p
    for( int i = l + 1 ; i <= r ; i ++ )
        if( arr[i] < arr[l] )
            swap(arr[i], arr[++j]);

    swap(arr[l], arr[j]);

    return j;
}

// 求出arr[l...r]范围里第k小的数
template <typename T>
int __selection( T arr[], int l, int r, int k )
{
    if( l == r )
        return arr[l];

    // partition之后, arr[p]的正确位置就在索引p上
    int p = __partition( arr, l, r );

    if( k == p )    // 如果 k == p, 直接返回arr[p]
        return arr[p];
    else if( k < p )    // 如果 k < p, 只需要在arr[l...p-1]中找第k小元素即可
        return __selection( arr, l, p-1, k);
    else // 如果 k > p, 则需要在arr[p+1...r]中找第k-p-1小元素
         // 注意: 由于我们传入__selection的依然是arr, 而不是arr[p+1...r],
         //所以传入的最后一个参数依然是k, 而不是k-p-1
        return __selection( arr, p+1, r, k );
}

// 寻找arr数组中第k小的元素
// 注意: 在我们的算法中, k是从0开始索引的, 即最小的元素是第0小元素, 以此类推
// 如果希望我们的算法中k的语意是从1开始的, 只需要在整个逻辑开始进行k--即可, 可以参考selection2
template <typename T>
int selection(T arr[], int n, int k) 
{
    assert( k >= 0 && k < n );

    srand(time(NULL));
    return __selection(arr, 0, n - 1, k);
}

// 寻找arr数组中第k小的元素, k从1开始索引, 即最小元素是第1小元素, 以此类推
template <typename T>
int selection2(T arr[], int n, int k) 
{
    return selection(arr, n, k - 1);
}

　　以上为通过熟悉的排序算法解决实际问题的示例，熟悉基础的算法，对算法进行延申可以解决众多实际问题。