选择排序、插入排序、冒泡排序、希尔排序

简介

以下总结几个基础的排序算法，包括选择排序、插入排序、冒泡排序、希尔排序，这几个排序算法是比较简单的几个。以下给出算法的分析和代码示例。

时间复杂度

选择排序、插入排序、冒泡排序、希尔排序四个排序算法的时间复杂度都是O(n^2)。

算法分析

选择排序

选择排序取第一个元素以此与后续的元素进行比较，保存最小的元素的下标，最终把最小的元素与第一个元素进行交换，第二次遍历取第二个元素，在剩余元素中选择最小的元素与第二个元素交换，依次类推。。。。，最终实现把所有元素按照从小到大进行排序。

以下为代码示例

template<typename T>
void selectionSort(T arr[], int n){

    for(int i = 0 ; i < n ; i ++){

        int minIndex = i;
        for( int j = i + 1 ; j < n ; j ++ )
            if( arr[j] < arr[minIndex] )
                minIndex = j;

        swap( arr[i] , arr[minIndex] );
    }
}

选择排序是基础的排序算法，但需要重点理解，以后复杂的算法也都会以此为基础进行衍生。

 

插入排序

插入排序分为两种，第一种是直接插入排序，第二种是折半插入排序，以下分别描述两种排序的基本思想：

直接插入排序的基本思想：当插入第i（i>1）个元素时，前面的data[0],data[1]……data[i-1]已经排好序。这时用data[i]的排序码与data[i-1],data[i-2],……的排序码顺序进行比较，找到插入位置即将data[i]插入，原来位置上的元素向后顺序移动。

折半插入排序的基本思想：设元素序列data[0],data[1],……data[n-1]。其中data[0],data[1],……data[i-1]是已经排好序的元素。在插入data[i]时，利用折半搜索法寻找data[i]的插入位置。

因为插入排序每次循环比较可能提前退出，所以比选择排序在性能上更优，特别是对于一些近乎有序的数据，插入排序的性能更优，插入排序对小数据量排序性能更好。

以下代码为直接插入排序的示例：

template<typename T>
void insertionSort(T arr[], int n)
{
	for(int i = 1; i < n; i++)
	{
		T tmp = arr[i];
		int j;
		for(j = i; j > 0 && arr[j - 1] > tmp; j --)
			arr[j] = arr[j - 1];

		arr[j] = tmp;
	}
}

 

冒泡排序

冒泡排序是进行两两比较，通过遍历一遍所有的数据把最大的元素放到最后，然后继续两两比较剩余的数据，依次类推，直到所有的数据都有序。冒泡排序与插入排序类似，对于几乎有序的数据，性能会更高。代码如下：

template<typename T>
void bubbleSort(T arr[], int n)
{
　　int newn;
　　do
　　{
　　　　newn = 0;
　　　　for(int i = 1; i < n; i++)
　　　　　　if(arr[i - 1] > arr[i])
　　　　　　{
　　　　　　　　swap(arr[i - 1], arr[i]);

　　　　　　　　//记录最后一次交换的位置，在此之后的元素在下一轮比较中均不考虑
　　　　　　　　newn = i;
　　　　　　}
			
　　　　　　n = newn;
　　　}while(newn > 0);
}

 

希尔排序

希尔排序的基本思想：

（1）希尔排序（shell sort）这个排序方法又称为缩小增量排序，是1959年D·L·Shell提出来的。该方法的基本思想是：设待排序元素序列有n个元素，首先取一个整数increment（小于n）作为间隔将全部元素分为increment个子序列，所有距离为increment的元素放在同一个子序列中，在每一个子序列中分别实行直接插入排序。然后缩小间隔increment，重复上述子序列划分和排序工作。直到最后取increment=1，将所有元素放在同一个子序列中排序为止。

（2）由于开始时，increment的取值较大，每个子序列中的元素较少，排序速度较快，到排序后期increment取值逐渐变小，子序列中元素个数逐渐增多，但由于前面工作的基础，大多数元素已经基本有序，所以排序速度仍然很快。

 

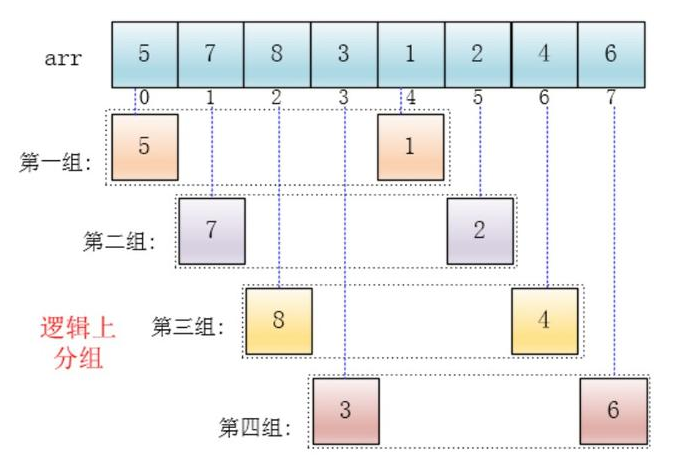
希尔排序的复杂度和增量序列是有关的

{1,2,4,8,...}这种序列并不是很好的增量序列，使用这个增量序列的时间复杂度（最坏情形）是O(n^2)

Hibbard提出了另一个增量序列{1,3,7，...,2^k-1}，这种序列的时间复杂度(最坏情形)为O(n^1.5)

Sedgewick提出了几种增量序列，其最坏情形运行时间为O（n^1.3）,其中最好的一个序列是{1,5,19,41,109,...}

 

示例代码如下：

template<typename T>
void InsertSort(T arr[], int h, int i)
{
	T tmp = arr[i]; 
	int j;
	for(j = i; j >= h && arr[j - h] > tmp; j -= h)
		arr[j] = arr[j - h];

	arr[j] = tmp;
}

template<typename T>
void shellSort(T arr[], int n)
{
	int h = 1;
	// 计算 increment sequence: 1, 4, 13, 40, 121, 364, 1093...
	while(h < n/3)
		h = 3 * h + 1;

	while(h >= 1)
	{
		//arr[h], arr[h+1], arr[h+2]....开始排序
		for(int i = h; i < n; i++)
		{
			//对arr[i], arr[i-h],...进行插入排序
			InsertSort(arr, h, i);
		}
		h /= 3;
	}
}