狄利克雷过程(Dirichlet Process)
先从狄利克雷过程的motivation开始说起,如果我们有一些数据,这些数据是从几个高斯分布中得出的,也就是混合高斯模型中得出的,比如下图这样
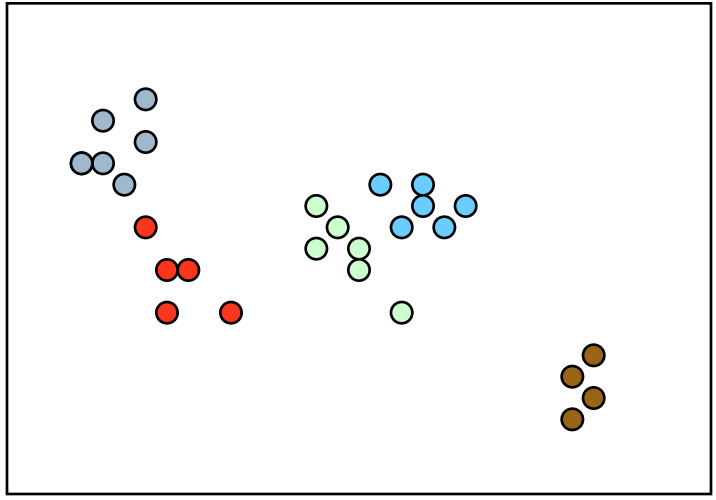
但是呢,我们并不知道混合高斯模型中到底有多少个高斯分布,它可能是这样
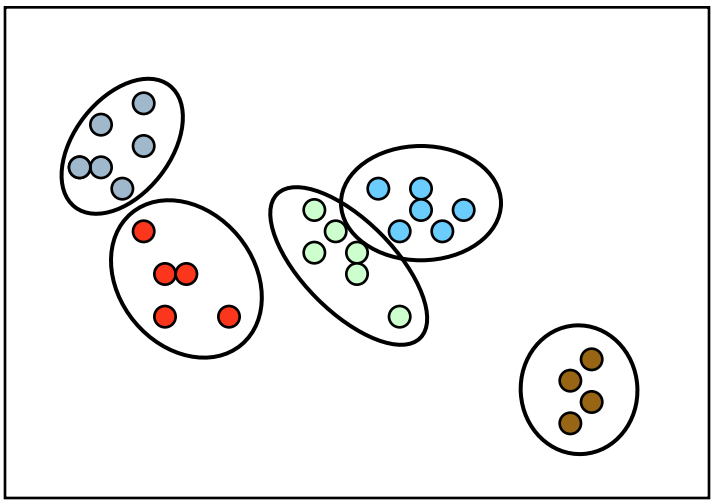
也可能是这样
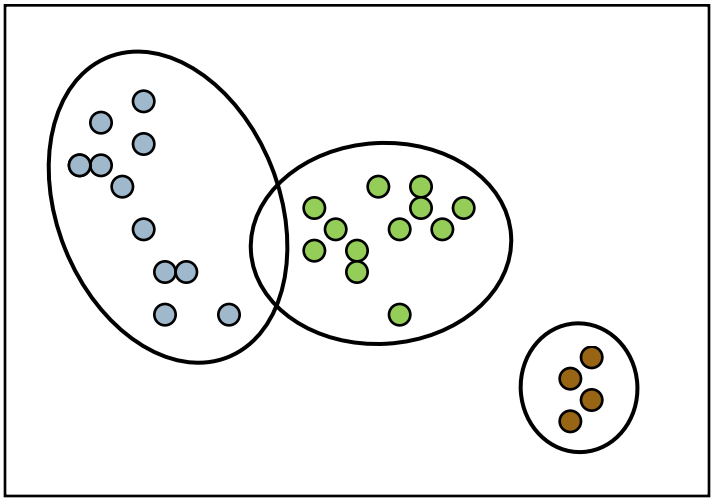
在这个情况下,最大期望算法并不能解决这个问题,所以我们就需要狄利克雷过程来帮助我们。现实生活中的例子可以是,我有一堆论文但是我不知道这些论文到底讨论了多少论题。
首先,需要明确的是我们使用狄利克雷过程是想解决聚类的问题,有多少类我并不知道。我们从最极端的例子开始考虑,假设有 个数据
,每个数据都是从不同的分布产生的
。那么,每一个分布会有对应自己的参数
,例如
是高斯分布,那么
。 既然,
是分布
产生的,
又可以用
来定义,那么我们可以对
建模。假设
是遵循某一个分布
,我们想想当
是连续分布的时候
,这也就是我之前假设的,每个数据都来自不同的分布。但是,这个假设并不是我们想要的,我们想要解决的是聚类问题。所以,我们就想到构造一个离散的分布
使得
,而且
要和
长得非常像。这个离散分布
就服从狄利克雷过程,也就是
。狄利克雷过程里的
,就是我之前提到的
也称作base measure,且不一定是连续的,也可以是离散的。
是一个矢量且
,可以理解为离散程度:如果
很大代表非常不离散,当
的时候
,
小就代表非常的离散,当
的时候,我们就是在用一个分布来对所有的
建模。这里我需要说一下,为了解释的简单一点,这样解释其实不是非常的准确,但是这样理解是没有问题的。
讲到这里,我必须提醒一下大家, 是从狄利克雷过程中产生的,不是一个随机变量而是一整个离散分布。
这里我讲完了狄利克雷过程的大致理解,接下来说狄利克雷过程具体是怎么定义的,和狄利克雷过程与狄利克雷分布的一些联系。
假设 都是从同一个狄利克雷过程中产生的,那么他们必然是有某一些内在的联系,至少得长得比较像。如下图,这两个分布,都是是从
过程中产生的。我们将这两个分布,分成
个不同的区域
,这个可以任意划分
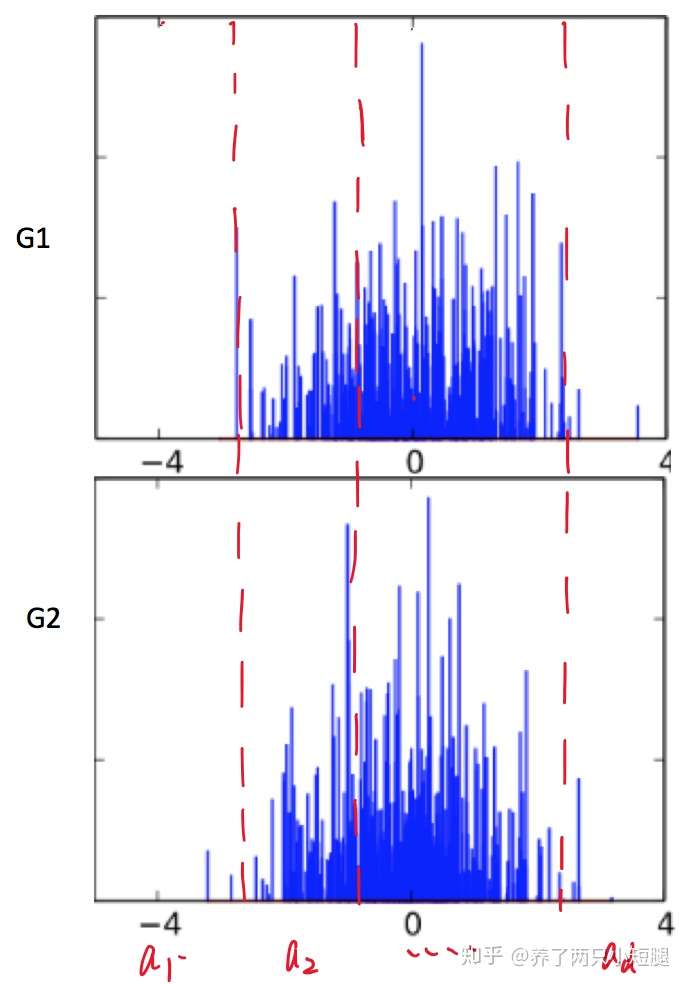
重申一下, 都是完整的分布,所以
从图中,我们也可以看出,每一个区域,长相都是略有相似的,所以我们定义:
以上其实就是狄利克雷过程的定义。也就是说 在每一个空间
里面的测度都要服从一个狄雷克雷分布。
以上就讲完了狄利克雷过程的定义,其实呢还想讲一讲狄利克雷过程的一些性质,因为确实有一些非常有意思的性质,也对我前面狄利克雷过程的解释有一些呼应。
随手百度就可以知道如果 ,则
,
根据狄利克雷过程的定义,
我们将 带入狄利克雷分布的期望和方差式子里面我们可以看到
因为
是一个分布,
从上面的式子中,首先我们可以看到, 的期望是和
没有关系的,而且就是等于
,这也符合最开始我说过的,我们的目的是构造一个尽量和
相近的离散分布。同样,前面我也提到
代表了这个狄利克雷过程到底有多离散。当
,
也就是最不离散的情况。当
,
,结合
,是不是有点儿眼熟?对,就是伯努利分布。也就是说,要么有一个测度在
里面,要么就不在,这也就是最离散的情况。
链接:https://www.zhihu.com/question/31398469/answer/533132532
DP的构造:stick breaking (掰棍构造,断棒过程)
是从
这个分布中产生的,它的位置和DP中的
参数无关,但是它的权重πi和
有关。βi~Beta(1,α) 服从Beta分布,范围为(0,1)
π1 = β1,π2= (1 - π1)*β2,... 第一根棍子的长度为权重值,第二根棍子的长度为剩余长度*权重值
E[βi] = 1/1+α , 如果α=0,说明第一次采样的时候,就把所有的权重都给第一个样本,对应只有一根棍子,也就是说G是最离散的版本(用一个值来代表整个分布)
当α趋于无穷,每个θ都是一个很小的权重,也就是说G=H。
G~DP(α,H)
θ~G
xi~F(θ)
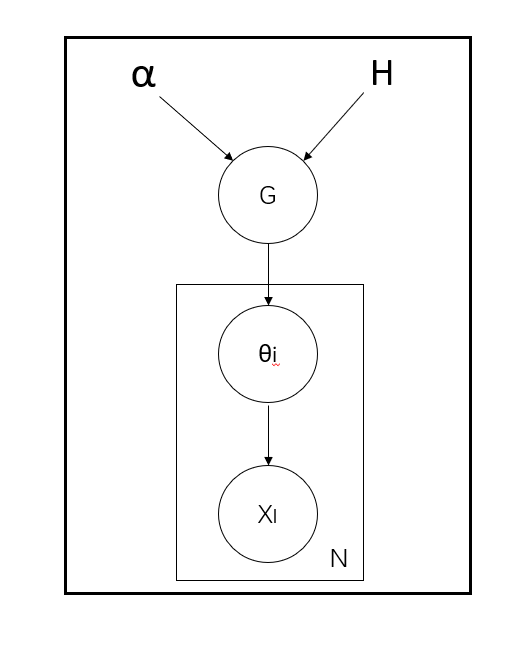
迪利克雷过程的性质:
G~DP(a,H) <=> (G(a1),...G(ak)) ~ DIR(aH(a1),...,aH(ak))
P(G|θ1.....θn) : G的后验
P(θ1.....θn|G):G的先验,因为G是一个分布,所以先验就为G
P(G):多项式似然函数
根据贝叶斯理论 ,P(G|θ1.....θn) 正比与 P(θ1.....θn|G) * P(G)
一个离散的分布P服从DIR迪利克雷分布,数据n1...nk服从多项式分布
(P1,...PK)~DIR(a1,...,ak)
(n1,...,nk)~mult(P1,...PK)
那么P(P1,...PK|n1,...,nk) = DIR(a1+n1,...,ak+nk)
类比下来
P(G(a1),...G(ak) | n1,...,nk) 正比与mult(n1,...,nk | G(a1),...G(ak))* DIR(aH(a1),...,aH(ak)) = DIR(aH(a1)+a1,...,aH(ak)+ak)
根据这个性质:G~DP(a,H) <=> (G(a1),...G(ak)) ~ DIR(aH(a1),...,aH(ak))
 δ是狄拉克函数,在集合里面取1,在集合外面取0,集合在这里是指基分布(H)被划分成的区间,\delta δ就是统计有多少atom落在每个区间的个数。
δ是狄拉克函数,在集合里面取1,在集合外面取0,集合在这里是指基分布(H)被划分成的区间,\delta δ就是统计有多少atom落在每个区间的个数。
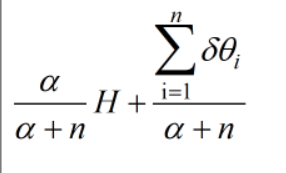 为一个连续的分布+一个离散的分布(称为 stick and slab)
为一个连续的分布+一个离散的分布(称为 stick and slab)





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 上周热点回顾(3.3-3.9)
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· AI 智能体引爆开源社区「GitHub 热点速览」