【洛谷P3372】【模板】线段树 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.求出某区间每一个数的和

输入输出格式

输入格式：

 

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

 

输出格式：

 

输出包含若干行整数，即为所有操作2的结果。

 

输入输出样例

输入样例#1：

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出样例#1：

11
8
20

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^，保证在int64/long long数据范围内）

样例说明：

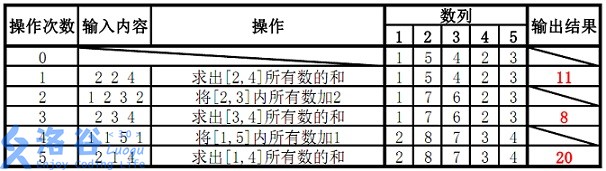
分析

此题同codevs1082线段树练习3。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=200000+5;
typedef long long ll;
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}
int n,m,len;
int a[maxn];
struct node
{
    int l,r,lc,rc,add;
    ll c;
}tr[maxn<<1];
inline void bt(int x,int y)
{
    len++; int now=len;
    tr[now].l=x; tr[now].r=y;
    if(x==y) tr[now].c=a[x];
    else
    {
        int mid=(x+y)>>1;
        tr[now].lc=len+1; bt(x,mid);
        tr[now].rc=len+1; bt(mid+1,y);
        tr[now].c=tr[tr[now].lc].c+tr[tr[now].rc].c;
    }
}
inline void pushdown(int now)
{
    int lc=tr[now].lc,rc=tr[now].rc;
    tr[lc].c+=tr[now].add*(tr[lc].r-tr[lc].l+1);
    tr[rc].c+=tr[now].add*(tr[rc].r-tr[rc].l+1);
    tr[lc].add+=tr[now].add;
    tr[rc].add+=tr[now].add;
    tr[now].add=0;
}
inline void update(int now,int x,int y,int k)
{
    if(tr[now].l==x&&tr[now].r==y)
    {
        tr[now].c+=k*(tr[now].r-tr[now].l+1);
        tr[now].add+=k;
    }else 
    {
        int lc=tr[now].lc,rc=tr[now].rc;
        pushdown(now);
        int mid=(tr[now].l+tr[now].r)>>1;
        if(y<=mid) update(lc,x,y,k);
        else if(x>=mid+1) update(rc,x,y,k);
        else {update(lc,x,mid,k); update(rc,mid+1,y,k);}
        tr[now].c=tr[lc].c+tr[rc].c;
    }
}
inline ll query(int now,int x,int y)
{
    if(tr[now].l==x&&tr[now].r==y) return tr[now].c;
    else 
    {
        int lc=tr[now].lc,rc=tr[now].rc;
        pushdown(now);
        int mid=(tr[now].l+tr[now].r)>>1;
        if(y<=mid) return query(lc,x,y);
        else if(x>=mid+1) return query(rc,x,y);
        else return query(lc,x,mid)+query(rc,mid+1,y);
    }
}
int main()
{
    n=read(); m=read();
    for(int i=1;i<=n;i++) a[i]=read();
    bt(1,n);
    for(int i=1;i<=m;i++)
    {
        int p,x,y,k;
        p=read();
        if(p==1)
        {
            x=read();y=read();k=read();
            update(1,x,y,k);
        }else if(p==2)
        {
            x=read();y=read();
            printf("%lld\n",query(1,x,y));
        }
    }
    return 0;
}