机器学习-3-线性回归

3.1基本形式

　　f(x)=w1x1+w2x2+....+wdxd+b

　　向量形式：f(x)=ω^Τx + b

　　线性回归试图学得f(x)=ω^Τx + b　，使得f(x_i) ≈ y_i (这里原著不是约等于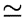，，是这个符号)

　　距离函数最小时，w，b的取值：

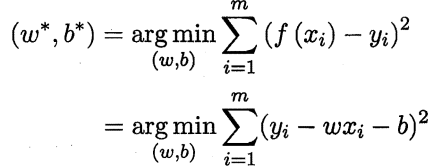
　　对距离函数求偏导数：

 

 

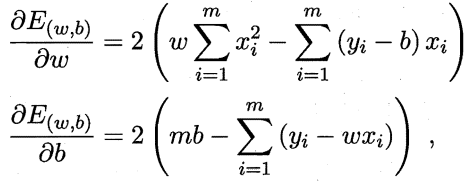
 　　然后，原著中是求偏导数为0的情况，类似于山峰顶部或者山峰底部的感觉。这是其中一种方法

　　第二种，我参考了吴达恩机器学习的课程，用的是梯度下降策略

　　即求偏导选定下降方向，使用基础的步长 a，

　　w = w - a*d_w

       b = b - a*d_b

　　这里a的选定很重要，选不好，有时是很难出结果的，a的建议可以是，0.0001，0.0003，0.0006，0.001，0.003，0.006，0.01这样的方案进行尝试

3.2线性回归代码

import numpy as np
import matplotlib.pyplot as plt

def plt_show(x,y,prt_w,prt_b):
    plt.scatter(x,y)
    plt.plot(x,prt_w*x+prt_b,c='red')
    plt.show()


#构造点
y=np.zeros(100)
x = np.random.rand(100)
suppose_b = 100
i=0
for i in range(100):
    x[i]=i+x[i]
    y[i]=x[i]*20+suppose_b+np.random.randint(-120,120)+np.random.random()
plt_show(x,y,20,100)
#假设初始线性函数
predict_w = 1
predict_b = 1

dis = 0
dist=[]
#梯度下降步长设置
a=0.0001

#40步
for i in range(40):
    # 构造偏导数
    d_w = np.mean((x * predict_w + predict_b - y) * x)
    d_b = np.mean(x * predict_w + predict_b - y)
    # 梯度下降
    predict_w = predict_w - a * d_w
    predict_b = predict_b - a * d_b
    # 构造距离函数
    dis = x * predict_w + predict_b - y
    disT = dis.T
    distance = dis.dot(disT)
    distance = distance / 100
    dist.append(distance)
    print('--------------')
print(predict_w)
print(predict_b)
print(dist)
plt_show(x,y,predict_w,predict_b)

具体我就不阐述了，有不明白可以去看原文。

参考文献：周志华《机器学习》，coursea-机器学习-吴达恩（这个b站也有），博客园的一位同学。