机器学习-5-神经网络

5.1  神经元模型

　　定义：神经网络（neural networks）是由具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应

　　神经元：神经网络的基本成分，在生物神经网络中，每个神经元之间相连，当它兴奋时，会向相邻的神经元发送化学物质，从而改变神经元内的电位；如果某神经元的电位超过了一个“阈值”（threshold），那么它就会被激活。

　　

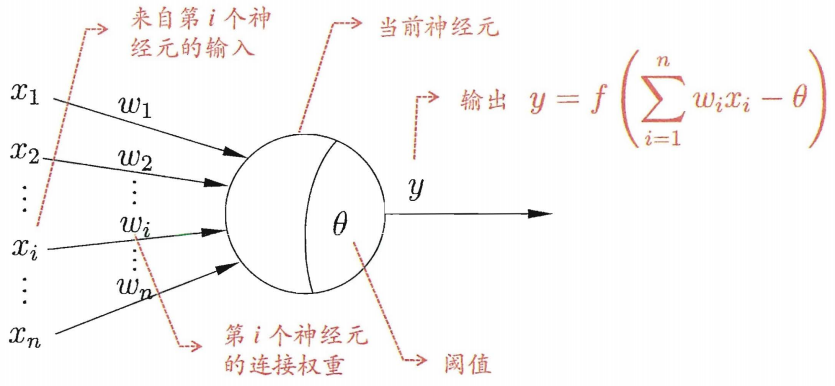
                                         M-P神经元模型

　　理想函数是阶跃函数，然而阶跃函数有不连续，不太光滑等不好的性质，因此实际常用函数为Sigmoid函数。

 

 

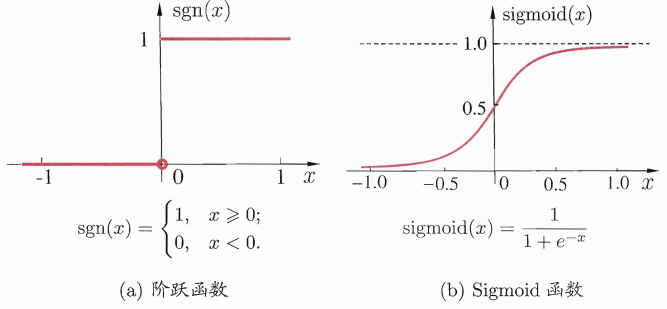
 　　将许多个这样的神经元连接，便得到了神经网络。

　　从计算机科学角度看，不必考虑神经网络是否模仿了生物神经网络，其自有数学证明在幕后支撑。

 

5.2  感知机与多层网络

　　感知机（Perceptron）由两层神经元组成，输入层接收外界信号后传递给输出层，输出层是M-P神经元，亦称“阈值逻辑单元”（threshold logic unit）

 

 　　感知机容易实现与或非运算。

5.3  误差逆传播算法

5.4  全局最小与局部最小

5.5  其他常见神经网络

5.6  深度学习

 

理论没写完，先上初版代码：(因为线性代数学艺不精，代码中求偏导部分的代码不是正经的矩阵求导，但是结果没错)

import math
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

'''
已知参数：x,y
未知参数：
输入层到隐层的权值  v
隐层到输出层的权值  w
隐层神经元的阈值    r
输出层神经元的阈值  θ
计算参数：
隐层神经元接受输入 a = v*x
隐层神经元输出     b
b = sigmoid( a - r )
输出层神经元接受输入β = w*b
输出层神经元输出 y = sigmoid(β-θ)
函数 sigmoid  f(x)=1/(1+e^(-x))

误差函数：wucha=(cy-ty)^2

给定学习步长 a, 对wucha函数， v,w,r,theta变量求偏导，进行迭代,使误差函数达到最小值。
'''
#仿神经网络函数
def sigmoid(x):
    return 1/(1+np.exp(-x))

#sigmoid函数的导数
def sigmoid_derivative(x):
    return x*(1-x)

#初始化四个参数v,r,w,theta
def initialize(number_x,number_y):
    v = np.ones(number_x*(number_x+1)).reshape(number_x,number_x+1)
    r = np.ones(number_x+1)
    w = np.ones(number_x+1)
    theta=np.ones(number_y)
    v = np.mat(v)
    r = np.mat(r)
    w = np.mat(w).T
    theta = np.mat(theta)
    return v,r,w,theta
    
def compute_y(x,v,r,w,theta):
    #计算隐层输入
    a = x*v
    #print('a')
    #print(a)
    #计算隐层输出
    b = sigmoid(a-r)
    #print('b')
    #print(b)
    #计算y层输入
    beta = b*w
    #print('beita')
    #print(beta)
    #计算y层输出
    y = sigmoid(beta-theta)
    #print('y')
    #print(y)
    return y

 
    
#参数根据梯度下降的迭代    
def diedai():
    return 0

def compute_wucha(cy,true_y):
    wucha = np.sum(np.square(true_y-cy))
    return wucha

def gradient_descent(learn,x,ty,v,r,w,theta):
    #计算隐层输入
    a = x*v
    #计算隐层输出
    b = sigmoid(a-r)
    #计算y层输入
    beta = b*w
    
    cy=compute_y(x,v,r,w,theta)

    e=np.mat([1,1,1,1])
    print('ty',ty,'cy',cy)
    g=np.multiply(np.multiply(cy,(1-cy)),(ty-cy))
    #对theta求偏导，以下几个求导都不属于正规的矩阵求导，结果没错
    theta_new=theta-learn*e*g
    print('theta_new',theta_new)
    
    #对w求偏导
    w_new=w+learn*np.multiply(g,b)*e.T
    print('w_new',w_new)
    
    #对r求偏导
    r_new=r-learn*e*np.multiply(np.multiply(b,(1-b)),np.multiply(w,g))
    print('r_new',r_new)
    
    #对v求偏导
    v_new=v+learn*x.T*np.multiply(np.multiply(b,(1-b)),np.multiply(w,g))
    print('v_new',v_new)
    cy_new=compute_y(x,v_new,r_new,w_new,theta_new)
    wucha=compute_wucha(cy_new,ty)
    print(wucha)
    return v_new,r_new,w_new,theta_new,wucha

if __name__ == '__main__':
    
    #给定学习率
    learn = 0.1
    #初始x
    x = np.mat([[1,1,2],[3,3,4],[2,3,4],[-1,-2,-3]])
    print('x',x)
    #现实y
    true_y=np.mat([1,1,1,0]).T
    #初始化参数
    v,r,w,theta=initialize(3,1)
    print('v',v)
    print('---------')
    print('r',r)
    print('---------')
    print('w',w)
    print('---------')
    print('theta',theta)
    print('---------')
    #神经网络函数计算的y
    cy=compute_y(x,v,r,w,theta)
    #计算ture_y与compute_y的误差
    wucha=compute_wucha(cy,true_y)
    wucha_list=[]
    print(wucha)
    xzhou=[]
    for i in range(10000):
        v,r,w,theta,wucha=gradient_descent(learn,x,true_y,v,r,w,theta)
        wucha_list.append(wucha)
        xzhou.append(i)
    print(wucha_list)

plt.plot(xzhou,wucha_list)
plt.show()

　　

 

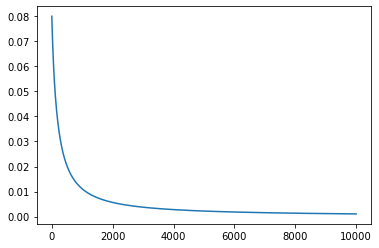
未完待续