使用 TF-IDF 加权的空间向量模型实现句子相似度计算
使用 TF-IDF 加权的空间向量模型实现句子相似度计算

字符匹配层次计算句子相似度
计算两个句子相似度的算法有很多种,但是对于从未了解过这方面算法的人来说,可能最容易想到的就是使用字符串匹配相关的算法,来检查两个句子所对应的字符串的字符相似程度。比如单纯的进行子串匹配,搜索 A 串中能与 B 串匹配的最大子串作为得分,亦或者用比较常见的最长公共子序列算法来衡量两个串的相似程度,使用编辑距离算法来衡量等。
上述基于字符匹配层次的算法一定程度上都可以计算出两个句子的相似度,不过他们只是单纯的从字符角度来计算,但是我们的句子都是有一定含义的,且句子中的每个词不应当被视为无关字符组合,而是不可分割的一个实体。所以这就需要对句子进行 分词 操作。在分词后,基于字符匹配的算法就应当以词组为单位进行匹配而不是单个字符。
向量空间模型
空间向量模型首先要对待处理的两个句子进行分词,这将会得到两个由 词 组成的序列。比如两个句子:
A:你怎么样? B:你还好吗?
分词后的结果就为:
A:["你","怎么样"]
B:["你","还好吗"]
然后将两个列表取并集得到列表 C:["你","怎么样","还好吗"];如果将 C 中的每一项(即一个词) 出现 标记为 1 ,不出现 标记为 0,那么这样离散化处理后,每一项所有的取值组合就构成了一个三维向量空间(实际上是空间中的八个点,因为是离散值)。像这样:
[1,1,1],[1,0,1],[0,0,1] ...;
此时再考虑 A 句子与 B 句子对应的两个词组列表,同样可以这样处理,得到两个三维向量(注意A、B要升到三维):
C:["你", "怎么样", "还好吗"]
A:["你", "怎么样" ]
A:[1, 1, 0 ]
C:["你", "怎么样", "还好吗"]
B:["你", "还好吗" ]
B:[1, 0, 1 ]
此时如果我们要计算这两个句子的相似度的话,事情就变得很简单了,只需要计算 A、B 两个向量的夹角即可。因为我们知道,当两个向量完全相同时,代表两个句子完全相同,此时两个向量的夹角为 0°,两个向量完全不同(无关)时,其夹角为 90°。一般计算两个向量的余弦值要比计算角度更容易(余弦值越大角度越小),所以计算两个句子相似度的问题就转化为计算两个 n 维向量的余弦值问题,问题被简化很多。而且引入空间向量模型的另一个好处就是,将原问题转化为数学模型,这样就可以带入数学的体系,利用很多强大的数学工具。
比如,引入词的统计信息,为每个分量加权。
使用 TF-IDF 算法为分量加权
TF-IDF 算法原理
TF-IDF 算法主要由两个概念组成,分别是 TF、IDF,我想可以用两句话来分别简单概括:
TF(词频):重要的事情说三遍。
IDF(逆文档频率):脚踩几条船应该是渣男。
以上两条均对一个句子中的某个词而言。
TF (Term Frequency),描述的是一个词在一个文档中出现的频率。如句子:”我喜欢吃苹果,你喜欢吃什么?“该句话中“喜欢”一词的频率即为 2/句子总词数;所以可知:$$TF = \frac{词 wi 在文档 D 中出现的次数}{文档 D 的总词数}$$ (注:在句子相似度计算中,不区分句子与文档,认为一个句子即为一篇文档)
TF 可以用来确定一个词从统计角度来说对一句话的重要性,比如:“记得吃早饭,早饭,早饭!” 显然这句话重复了三次“早饭”,即该词的词频较大,所以可以认为这句话中“早饭”是十分重要的词。
而 IDF(Inverse Document Frequency) 描述的是一个词在所有句子中出现的次数。如果一个词在很多句子都出现过,那么可以认为,这个词通用性较强,所以不具备一定的区分能力,像“东西”,“相信”,“可以” 等等。IDF 的计算公式为:$$IDF = log(\frac{语料库中的所有文档数}{包含词 wi 的文档数+1})$$ ,其中分式用来衡量“脚踏几条船”的程度,而 log 函数,据说该算法作者也未明确给出理论论述,应该属于信息论范畴(对信息论知之甚少,希望以后有机会了解并解释)。最后的 TF-IDF 的公式为 $$TF*IDF$$ ,将此值作为一个句子词组向量的某个分量的权值。
接下来讲讲通过加权后,原来的空间向量模型发生了什么变化。
加权后的空间向量模型
首先做一个直观对比:
加权前:[1, 0, 1, 1, 0, 1]
加权后:[0.21, 3.12, 1, 0, 1.2, 1]
加权后的每个分量的取值发生了变化。未加权前每个分量的取值为 {0,1} 表示一个词的有无,而加权后取值为 {0,weight} ,表示一个词或者无,或者存在且有自己对于所属句子的重要性(注意:仍是离散的两个量)。为了便于演示和理解,现在使用二维的向量做加权前与加权后在计算句子相似度(即计算向量余弦值)上的比较。
未加权的二维向量取值可表示为如下图:
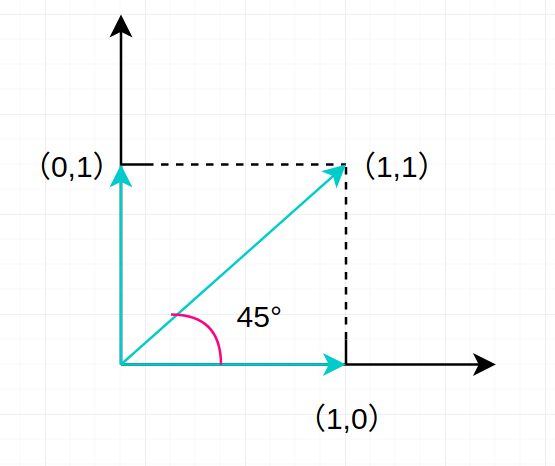
由于两个分量只能分别取 0,1,所以句子的词组向量 [1,1] 与 [1,0] 所成夹角为 45°。相似度为 \(\frac{\sqrt{2}}{2}\) 。
给其中一个分量加权后的向量取值可表示为下图:
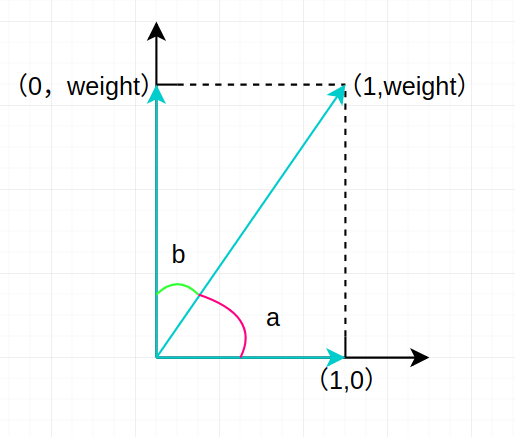
现在我们通过加权算法给一个句子词组向量中的某个分量以 weight 且 weight > 1,此时我们要做两个对比,分别是向量 [0,weight] 与 [1,weight] 、向量 [1,weight] 与 [1,0] 。 通过对比我们将看到 weight 权重所代表的词对于计算两个句子相似度的影响。
先考虑向量 [0,weight] 与 [1,weight]。
这两个向量由于有一个相同的词,weight 权重对应的词,从上图中可以看出(亦可证明出)二者成的一个夹角 b 要小于 45°,即这两个词组向量所代表的句子相似度要大于未加权时的相似度。
再考虑向量 [1,weight] 与 [1,0]。
这两个向量没有相同的 weight 权重对应的词,而从上图中可以看出(亦可证出) a 的角度要大于 45°,即这两个词组向量算所代表的句子的相似度要小于未加权时的相似度。
所以结论就是,当我们给一个句子中的某个词一个权值,这个权值表示该词从语料库中区分出其所在句子的能力,这样加权后,当待考察的两个句子如果同时包含了一个词 wi,无论这个 wi 对于其中那个句子有较高的权值,此时都会基于单纯的空间向量模型之上增大两个句子的相似度。相反,如果二者不同时包含词 wi ,就会基于空间向量模型减少二者相似度。可以说,通过 TF-IDF 为句子词组向量加权后,空间向量模型融入了统计信息,增加了计算两个句子相似度的准确性。
TF-IDF 算法特点
TF-IDF 算法计算句子相似度具有执行速度快的优点,对于长句子、长文本效果较好,因为句子越长统计信息越多。对于短文本可能效果稍差一些,但即便这样仍不会退化为普通的向量空间模型,因为即便 TF 退化,仍有 IDF 统计整个语料库的数据,仍然可以影响权重。
结语
本文内容基于个人理解,所学有限,若有任何错误、问题,欢迎指出、讨论。
下一篇文章将讨论该算法的实现。
作者:Skipper
出处:https://www.cnblogs.com/backwords/p/12321390.html
本博客中未标明转载的文章归作者 Skipper 和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号