2024熵密杯wp

第一部分：初始谜题

这一部分算是开胃菜，形式也更像平时见到的CTF题目，三个题目都是python加密的，做出其中任意一个就可以进入第二部分，也就是一个更类似真实情境的大型密码渗透系统。

但每个初始谜题都是有分数的，所以就算开了第二部分也当然要接着做。

每个题目也都有前三血的加成，一血5%，二血3%，三血1%，在最后排名的时候会先根据分数再根据解题时间，所以血量分其实很重要，但是手速实在不太够

然后就是他每个初始谜题下发的附件不仅包含加密用的.py文件，还有一个.exe文件，开启实例并输入ip和端口，之后题目就会下发加密数据，与他进行正确交互后就能拿到flag了。

初始谜题一(300 pts)

题目：

from sympy import Mod, Integer
from sympy.core.numbers import mod_inverse

# 模数
N_HEX = "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123"
MODULUS = Integer(int(N_HEX, 16))
MSG_PREFIX = "CryptoCup message:"


# 加密函数
def encrypt_message(message, key):
    # 添加前缀
    message_with_prefix = MSG_PREFIX + message
    message_bytes = message_with_prefix.encode('utf-8')
    message_len = len(message_bytes)
    num_blocks = (message_len + 15) // 16
    blocks = [message_bytes[i * 16:(i + 1) * 16] for i in range(num_blocks)]

    # 进行0填充
    blocks[-1] = blocks[-1].ljust(16, b'\x00')

    encrypted_blocks = []

    k = key

    # 加密每个分组
    for block in blocks:
        block_int = int.from_bytes(block, byteorder='big')
        encrypted_block_int = Mod(block_int * k, MODULUS)
        encrypted_blocks.append(encrypted_block_int)
        k += 1  # 密钥自增1

    # 将加密后的分组连接成最终的密文
    encrypted_message = b''.join(
        int(block_int).to_bytes(32, byteorder='big') for block_int in encrypted_blocks
    )

    return encrypted_message


# 解密函数
def decrypt_message(encrypted_message, key):
    num_blocks = len(encrypted_message) // 32
    blocks = [encrypted_message[i * 32:(i + 1) * 32] for i in range(num_blocks)]

    decrypted_blocks = []

    k = key

    # 解密每个分组
    for block in blocks:
        block_int = int.from_bytes(block, byteorder='big')
        key_inv = mod_inverse(k, MODULUS)
        decrypted_block_int = Mod(block_int * key_inv, MODULUS)
        decrypted_blocks.append(decrypted_block_int)
        k += 1  # 密钥自增1

    # 将解密后的分组连接成最终的明文
    decrypted_message = b''.join(
        int(block_int).to_bytes(16, byteorder='big') for block_int in decrypted_blocks
    )

    # 去除前缀
    if decrypted_message.startswith(MSG_PREFIX.encode('utf-8')):
        decrypted_message = decrypted_message[len(MSG_PREFIX):]

    return decrypted_message.rstrip(b'\x00').decode('utf-8')


# 测试
initial_key = Integer(0x123456789ABCDEF0123456789ABCDEF0123456789ABCDEF0123456789ABCDEF0)
message = "Hello, this is a test message."
print("Original Message:", message)

# 加密
encrypted_message = encrypt_message(message, initial_key)
print("Encrypted Message (hex):", encrypted_message.hex())

# 解密
decrypted_message = decrypt_message(encrypted_message, initial_key)
print("Decrypted Message:", decrypted_message)

题目加密流程大概如下：

有一个未知的initial_key，与一个未知的message
对于这个message，题目会在他前面填上一个固定的前缀”CryptoCup message:”，并在最后补充上”\x00”使得整个消息长为16的倍数
将填充了前后缀的消息按16字节为一组分组
从第一个分组开始，将该分组消息转化为整数，记为mi，并计算：

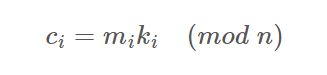
其中ki是key在对应分组的值(key每个分组之后会自增一)

将所有ci转成32字节，并连接在一起得到密文

靶机只会发送encrypted_message，要发送给他message来拿到flag。这个可以说是相当轻松了，由于有一个已知的前缀，并且他超过了16字节，因此就有第一个分组对应的明文和密文，所以就可以直接求出key来。

exp：

from Crypto.Util.number import *

N_HEX = "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123"
MODULUS = int(N_HEX, 16)
MSG_PREFIX = b"CryptoCup message:"

c = bytes.fromhex("a7ea042608ffce5be79a19ee45533506819e85f8d9250fccef5a89731151fd7a76d83aa85c47ba1357a86d0e9763470fb608cd54d0927125f500353e156a01da759fa814e96fa41a888eea3a9cf9b062923ed70774add490c7ed7f83d6b47e711e7b3c8a960dcc2838e577459bb6f2769d0917e1fd57db0829633b77652c2180")
C = [c[32*i:32*i+32] for i in range(len(c)//32)]

msg = b""
key = bytes_to_long(C[0]) * inverse(bytes_to_long(MSG_PREFIX[:16]), MODULUS) % MODULUS
for i in range(len(C)):
    msg += long_to_bytes(bytes_to_long(C[i]) * inverse(key,MODULUS) % MODULUS)
    key += 1
print(msg)


#CryptoCup message:dHyNBCgxEq4prNBbxjDOiOgmvviuAgfx\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\

发送message回去之后就会拿到flag，以及一个登录Gitea的帐号密码：

验证通过
flag{OYLXbASQsEc5SVkhBj7kTiSBc4AM5ZkR}
gitea账号：giteauser2024
gitea口令：S(*HD^WY63y89TY71
提示：gitea账号和口令用于登录第二环节的gitea服务器，请注意保存！

后面两个初始谜题也都是给一个拿分的flag，以及一个账号密码作为开第二部分的钥匙，所以后面两个初始谜题就不写这个了

初始谜题二(300 pts)

题目：

import binascii
from gmssl import sm3


# 读取HMAC key文件
def read_hmac_key(file_path):
    with open(file_path, 'rb') as f:
        hmac_key = f.read().strip()
    return hmac_key


# 生成token
def generate_token(hmac_key, counter):
    # 如果HMAC_KEY长度不足32字节，则在末尾补0，超过64字节则截断
    if len(hmac_key) < 32:
        hmac_key = hmac_key.ljust(32, b'\x00')
    elif len(hmac_key) > 32:
        hmac_key = hmac_key[:32]

    # 将计数器转换为字节表示
    counter_bytes = counter.to_bytes((counter.bit_length() + 7) // 8, 'big')
    # print("counter_bytes:", binascii.hexlify(counter_bytes))

    tobe_hashed = bytearray(hmac_key + counter_bytes)

    # print("tobe_hashed:", binascii.hexlify(tobe_hashed))

    # 使用SM3算法计算哈希值
    sm3_hash = sm3.sm3_hash(tobe_hashed)

    # 将SM3的哈希值转换为十六进制字符串作为token
    token = sm3_hash

    return token


current_counter = 0


def verify_token(hmac_key, counter, token):
    # 生成token
    generated_token = generate_token(hmac_key, counter)
    global current_counter
    # 比较生成的token和输入的token是否相同
    if generated_token == token:
        if counter & 0xFFFFFFFF > current_counter:
            current_counter = counter & 0xFFFFFFFF
            print("current_counter: ", hex(current_counter))
            return "Success"
        else:
            return "Error: counter must be increasing"
    else:
        return "Error: token not match"


# 假设HMAC key文件路径
hmac_key_file = 'hmac_key.txt'
# 假设计数器值
counter = 0x12345678

# 读取HMAC key
hmac_key = read_hmac_key(hmac_key_file)

# 生成token
token = generate_token(hmac_key, counter)
print("Generated token:", token)
print(verify_token(hmac_key, counter, token))

题目内容很简单：

读取一个未知的hmac_key，并生成一个随机的counter
将hmac_key控制在32字节(不足则填充”\x00”，超出则截断)
将hmac_key与counter拼接起来进行SM3哈希

然后下发的数据有：

SM3得到的哈希值
counter值

我们需要完成的事情是：

找到一个新的counter，使得新counter的低32位比原来的counter大
计算出hmac_key与新counter拼接后的SM3哈希值
发送新counter和这个哈希值就能拿到flag

看明白题意就会知道这是一个基于SM3的哈希长度扩展攻击，由于控制了hmac_key为32字节，并且counter只有4字节，而SM3的分组长度是64字节，所以说我们拿到的哈希值是只有一个分组的。而按照SM3的填充规则，这个分组哈希的完整分组其实是下面这部分内容的part1 + part2：(单引号代表字节串，双引号代表比特串)

#448 bits
part1 = 'hmac_key'(32 bytes) + 'counter'(4 bytes) + "1" + "00...0"

#64 bits
part2 = bin(8*(len(hmac_key + counter)))[2:].zfill(64)

这两部分拼起来就得到了完整的第一个分组。

SM3的哈希长度扩展攻击基于其Merkle Damgard结构，我们可以用一个已知分组的哈希值，去继续迭代计算更长的含有该分组消息的哈希值，而不需要知道这个分组对应的明文是什么。所以我们完全可以构造下面这样的counter：

New_counter = 'counter'(4 bytes) + "1" + "00...0" + bin(8*(len(hmac_key + counter)))[2:].zfill(64) + '\xff\xff\xff\xff'

那么hmac_key拼接上这个counter后，其用于SM3哈希的消息就会按64字节分为两组，而第一组是和靶机发送的消息完全一样的，因此我们就可以利用哈希长度扩展攻击迭代计算整个消息的哈希值了，具体实现代码是赛前那天晚上在github上随便找的：

KKrias/length-extension-attack-for-SM3 (github.com)

稍微对着题意改一改就好。

exp：

def zero_fill(a,n):
    if len(a)<n:
        a="0"*(n-len(a))+a
    return a
def cycle_shift_left( B, n):
    n=n%32
    return ((B << n) ^ (B >> (32 - n)))%(2**32)

def T(j):
    if j>=0 and j<=15:
        return int("79cc4519",16)
    elif j>=16 and j<=63:
        return int("7a879d8a",16)

def FF(X,Y,Z,j):
    if j>=0 and j<=15:
        return X^Y^Z
    elif j>=16 and j<=63:
        return (X&Y)|(X&Z)|(Y&Z)
def GG(X,Y,Z,j):
    if j >= 0 and j <= 15:
        return X ^ Y ^ Z
    elif j >= 16 and j <= 63:
        return (X & Y) | (~X & Z)

def P0(x):
    return x^(cycle_shift_left(x,9))^cycle_shift_left(x,17)
def P1(x):
    return x^(cycle_shift_left(x,15))^cycle_shift_left(x,23)

def Message_extension(a):  #a的数一定要满足512bit,不够要补零!!  ,承接的是字符串
    W1 = []            #  W0-15
    W2=[]             #  W' 0-63
    #print("a消息扩展的a:",a)
    for i in range(int(len(a) / 8)):
        W1.append(int(a[8 * i:8 * i + 8],16))
        #print("W1的前16个",a[8 * i:8 * i + 8])
    for j in range(16,68):
        temp=P1(W1[j-16] ^ W1[j-9] ^ cycle_shift_left(W1[j-3],15)) ^cycle_shift_left(W1[j-13],7)^W1[j-6]
        #print("消息扩展：",hex(temp))
        W1.append(temp)

    for j in range(0,64):
        W2.append(W1[j]^W1[j+4])

    W1.append(W2)
    return W1

def CF(V,Bi):  #V是字符串
    Bi=zero_fill(Bi,128)
    W=[]
    W=Message_extension(Bi)   #消息扩展完的消息字
    #print("W:",W)
    A=int(V[0:8],16)
    #print("A:", hex(A))
    B = int(V[8:16], 16)
    C = int(V[16:24], 16)
    D = int(V[24:32], 16)
    E = int(V[32:40], 16)
    F = int(V[40:48], 16)
    G = int(V[48:56], 16)
    H = int(V[56:64], 16)
    for j in range(0,64):
        temp=(cycle_shift_left(A,12) + E +cycle_shift_left(T(j),j)) %(2**32)
        SS1=cycle_shift_left(temp,7)
        SS2=SS1 ^ cycle_shift_left(A,12)
        TT1=(FF(A,B,C,j) +D +SS2 +W[-1][j] ) %(2**32)
        TT2=(GG(E,F,G,j)+H+SS1+W[j])%(2**32)
        D=C
        C=cycle_shift_left(B,9)
        B=A
        A=TT1
        H=G
        G=cycle_shift_left(F,19)
        F=E
        E=P0(TT2)
        #print("B:", hex(B))
    t1=zero_fill(hex(A^int(V[0:8],16))[2:],8)
    t2 = zero_fill(hex(B ^ int(V[8:16], 16))[2:], 8)
    t3 = zero_fill(hex(C ^ int(V[16:24], 16))[2:], 8)
    t4 = zero_fill(hex(D ^ int(V[24:32], 16))[2:], 8)
    t5 = zero_fill(hex(E ^ int(V[32:40], 16))[2:], 8)
    t6 = zero_fill(hex(F ^ int(V[40:48], 16))[2:], 8)
    t7 = zero_fill(hex(G ^ int(V[48:56], 16))[2:], 8)
    t8 = zero_fill(hex(H ^ int(V[56:64], 16))[2:], 8)
    t=t1+t2+t3+t4+t5+t6+t7+t8
    return t

def SM3(plaintext):
    Vtemp=IV
    a=(len(plaintext)*4+1 ) % 512
    #print(a)
    k=0
    B=[]
    if a<=448:
        k=448-a
    elif a>448:
        k=512-a+448
    #print(k)
    m=plaintext+"8"+"0"*int((k+1)/4-1)+zero_fill(str(hex(len(plaintext)*4))[2:],16)
    #print(m)
    block_len=int((len(plaintext)*4 + k + 65) / 512)
    #print(block_len)
    for i in range(0,block_len):
        B.append(m[128*i:128*i+128])     #分组
    #print("B:",B)
    for i in range(0,block_len):
        Vtemp=CF(Vtemp,B[i])

    return Vtemp

def SM3_len_ex_ak(num_block,IV,plaintext):
    Vtemp=IV
    a=(len(plaintext)*4+1 ) % 512
    #print(a)
    k=0
    B=[]
    if a<=448:
        k=448-a
    elif a>448:
        k=512-a+448
    #print(k)
    m=plaintext+"8"+"0"*int((k+1)/4-1)+zero_fill(str(hex(len(plaintext)*4+num_block*512))[2:],16)
    #print(m)
    block_len=int((len(plaintext)*4 + k + 65) / 512)
    #print(block_len)
    for i in range(0,block_len):
        B.append(m[128*i:128*i+128])     #分组
    #print("B:",B)
    for i in range(0,block_len):
        Vtemp=CF(Vtemp,B[i])

    return Vtemp

IV="7380166f4914b2b9172442d7da8a0600a96f30bc163138aae38dee4db0fb0e4e"


#############################################################################
IV2="c2427b818b1fb3b9e72e0ec8c60d101a17865842506e6b0052278a0c156d9e7a"
num_block=1
counter = "51f18456"
New_Counter = hex(int((bin(int(counter,16))[2:].zfill(32) + "1") + "0"*(448 - 32*8 - 1 - 4*8) + bin(36*8)[2:].zfill(64) , 2))[2:] + "ffffffff"

print(New_Counter)
print(SM3_len_ex_ak(1,IV2,"FFFFFFFF"))

#flag{3WhlSlIw4tSOhbY52j6CMrUCAYSLfrS9}

初始谜题三(300 pts)

题目：

import sympy as sp
import random

# 设置参数
n = 16  # 向量长度
q = 251  # 模数

# 生成随机噪声向量e
e = sp.Matrix(sp.randMatrix(n, 1, min=0, max=1))  # 噪声向量

# 生成随机n维私钥向量s和n*n矩阵A
s = sp.Matrix(sp.randMatrix(n, 1, min=0, max=q - 1))  # 私钥向量
Temp = sp.Matrix(sp.randMatrix(n, n, min=0, max=q - 1))  # 中间变量矩阵Temp
A = Temp.inv_mod(q)  # 计算矩阵Temp在模 q 下的逆矩阵作为A

# 计算n维公钥向量b
b = (A * s + e) % q  # 公钥向量b = A * s + e


# 加密函数
def encrypt(message, A, b):
    m_bin = bin(message)[2:].zfill(n)  # 将消息转换为16比特的二进制字符串
    m = sp.Matrix([int(bit) for bit in m_bin])  # 转换为SymPy矩阵
    x = sp.Matrix(sp.randMatrix(n, n, min=0, max=q // (n * 4)))  # 随机产生一个n*n的矩阵x
    e1 = sp.Matrix(sp.randMatrix(n, 1, min=0, max=1))  # 随机产生一个n维噪声向量e
    c1 = (x * A) % q  # 密文部分c1 =   x * A
    c2 = (x * b + e1 + m * (q // 2)) % q  # 密文部分c2 = x * b + e1 + m * q/2
    return c1, c2


# 解密函数
def decrypt(c1, c2, s):
    m_dec = (c2 - c1 * s) % q
    m_rec = m_dec.applyfunc(lambda x: round(2 * x / q) % 2)  # 还原消息
    m_bin = ''.join([str(bit) for bit in m_rec])  # 将SymPy矩阵转换为二进制字符串
    m_rec_int = int(m_bin, 2)  # 将二进制字符串转换为整数
    return m_rec_int


# 测试加解密
message = random.randint(0, 2 ** n - 1)  # 要加密的消息，随机生成一个16比特整数
c1, c2 = encrypt(message, A, b)  # 加密

print("原始消息: ", message)
print("公钥A=sp.", A)
print("公钥b=sp.", b)
print("密文c1=sp.", c1)
print("密文c2=sp.", c2)

decrypted_message = decrypt(c1, c2, s)
print("解密后的消息: ", decrypted_message)  # 输出解密

题目名字叫lwe，具体来说给了一些如下数据：

随机生成16维的01向量e
随机生成16维的向量s以及16x16的可逆矩阵A，并计算：
$b = A s + e$
将m转化为比特串，并进一步变为长度为16的01向量(也就是说m本身也只有2字节)

给出A、b、c1、c2，要求还原message并发送给他

虽然说题目叫lwe，似乎也可以通过lwe的方法求出s来，但是很显眼的一点是维数仅仅为16，实在太小了，只需要琼剧2^16其中就一定有正确的e、e1了。

然而再仔细看发现有更离谱的一点，既然A、c1都给好了并且A可逆，那么x直接求就好了，然后就可以轻松得到：

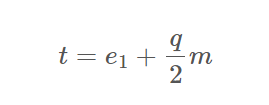
而由于e1也是01向量，他对向量t的大小影响可以忽略不计，所以t中大于等于q/2的位置就是m中为1的位置，否则就是0。

exp：

A = Matrix(ZZ,[[139, 63, 18, 202, 166, 185, 85, 108, 58, 90, 211, 248, 240, 44, 137, 39], [5, 230, 89, 226, 139, 24, 233, 20, 12, 108, 127, 11, 52, 64, 188, 156], [80, 61, 105, 3, 165, 96, 154, 40, 62, 103, 157, 75, 190, 101, 31, 239], [193, 100, 124, 216, 248, 95, 241, 196, 67, 192, 217, 114, 171, 248, 219, 169], [116, 71, 221, 105, 167, 153, 22, 124, 178, 45, 7, 183, 125, 8, 127, 123], [182, 162, 164, 184, 27, 148, 206, 73, 217, 86, 187, 137, 82, 150, 99, 65], [106, 60, 153, 91, 213, 41, 188, 92, 121, 246, 164, 223, 199, 85, 161, 25], [93, 97, 145, 31, 48, 36, 7, 110, 56, 47, 108, 79, 233, 186, 93, 181], [195, 98, 47, 147, 49, 40, 158, 89, 218, 8, 23, 118, 170, 19, 50, 17], [127, 95, 37, 48, 230, 244, 130, 37, 75, 125, 103, 154, 148, 218, 227, 178], [162, 235, 129, 44, 204, 228, 221, 130, 239, 36, 57, 38, 41, 74, 61, 155], [246, 11, 11, 97, 218, 57, 209, 72, 229, 27, 250, 73, 19, 64, 25, 62], [60, 162, 1, 110, 191, 130, 120, 227, 214, 98, 165, 245, 28, 55, 94, 190], [129, 212, 185, 156, 119, 239, 83, 221, 4, 174, 65, 218, 32, 211, 213, 223], [80, 218, 135, 245, 238, 127, 55, 68, 113, 145, 110, 59, 50, 177, 159, 146], [68, 239, 36, 166, 206, 23, 59, 126, 67, 152, 99, 189, 133, 113, 243, 198]])
b = Matrix(ZZ,[[88], [74], [219], [244], [81], [109], [81], [216], [125], [218], [170], [56], [152], [229], [204], [45]])
c1 = Matrix(ZZ,[[173, 2, 67, 11, 40, 80, 187, 38, 16, 226, 243, 79, 117, 127, 100, 113], [208, 231, 211, 196, 2, 146, 35, 2, 221, 119, 12, 25, 208, 152, 83, 201], [154, 43, 180, 76, 235, 5, 179, 196, 206, 171, 98, 145, 92, 144, 247, 98], [121, 145, 123, 232, 87, 78, 181, 145, 79, 166, 112, 169, 208, 102, 201, 63], [204, 141, 165, 225, 213, 137, 40, 43, 229, 151, 72, 237, 58, 15, 2, 31], [35, 114, 241, 31, 122, 123, 164, 231, 197, 89, 41, 236, 128, 22, 152, 82], [141, 133, 235, 79, 43, 120, 209, 231, 58, 85, 3, 44, 73, 245, 227, 62], [28, 158, 71, 41, 152, 32, 91, 200, 163, 46, 19, 121, 23, 209, 25, 55], [156, 17, 218, 146, 231, 242, 91, 76, 217, 57, 100, 212, 243, 87, 62, 159], [100, 111, 107, 62, 106, 72, 51, 79, 223, 93, 86, 145, 192, 21, 218, 243], [196, 250, 248, 166, 155, 39, 7, 93, 103, 54, 168, 188, 190, 104, 183, 64], [16, 131, 148, 193, 19, 149, 179, 212, 109, 170, 201, 168, 165, 167, 68, 25], [30, 222, 171, 32, 141, 105, 232, 104, 198, 53, 50, 157, 206, 165, 200, 42], [90, 149, 148, 112, 142, 228, 231, 119, 235, 248, 233, 9, 242, 102, 241, 93], [150, 32, 78, 183, 68, 249, 80, 165, 95, 229, 211, 0, 75, 14, 172, 139], [175, 69, 15, 100, 113, 63, 123, 71, 24, 250, 135, 232, 53, 32, 81, 117]])
c2 = Matrix(ZZ,[[18], [67], [187], [237], [99], [127], [128], [23], [83], [66], [64], [69], [7], [214], [43], [156]])

p = 251
A = Matrix(Zmod(p), A)
c1 = Matrix(Zmod(p), c1)
b = vector(b.T)
c2 = vector(c2.T)
x = c1*A^(-1)
t = c2 - x*b
m = ""
for i in t:
    if(i >= p // 2):
        m += "1"
    else:
        m += "0"
print(hex(int(m,2)))


#21c4

第二部分：大型密码系统

这一部分共有4个题目和一个最终挑战，题目之间是有顺序关系的，也就是要先做出某些题目，才能得到后续题目的附件、数据、登录密码之类的相关信息，具体来说这次挑战的先后顺序是：

flag1和flag3可以同时挑战
做出flag1可以开启flag2
做出flag3可以开启flag4
全部完成后可以开启最终挑战

flag1(600 pts)

题目：

passwordEncryptorV2.c：

#include <stdio.h>
#include <string.h>
#include <openssl/sha.h>

#define ROUND 16

//S-Box 16x16
int sBox[16] =
        {
                2, 10, 4, 12,
                1, 3, 9, 14,
                7, 11, 8, 6,
                5, 0, 15, 13
        };


// 将十六进制字符串转换为 unsigned char 数组
void hex_to_bytes(const char* hex_str, unsigned char* bytes, size_t bytes_len) {
    size_t hex_len = strlen(hex_str);
    if (hex_len % 2 != 0 || hex_len / 2 > bytes_len) {
        fprintf(stderr, "Invalid hex string length.\n");
        return;
    }

    for (size_t i = 0; i < hex_len / 2; i++) {
        sscanf(hex_str + 2 * i, "%2hhx", &bytes[i]);
    }
}


// 派生轮密钥
void derive_round_key(unsigned int key, unsigned char *round_key, int length) {

    unsigned int tmp = key;
    for(int i = 0; i < length / 16; i++)
    {
        memcpy(round_key + i * 16,      &tmp, 4);   tmp++;
        memcpy(round_key + i * 16 + 4,  &tmp, 4);   tmp++;
        memcpy(round_key + i * 16 + 8,  &tmp, 4);   tmp++;
        memcpy(round_key + i * 16 + 12, &tmp, 4);   tmp++;
    }
}


// 比特逆序
void reverseBits(unsigned char* state) {
    unsigned char temp[16];
    for (int i = 0; i < 16; i++) {
        unsigned char byte = 0;
        for (int j = 0; j < 8; j++) {
            byte |= ((state[i] >> j) & 1) << (7 - j);
        }
        temp[15 - i] = byte;
    }
    for (int i = 0; i < 16; i++) {
        state[i] = temp[i];
    }
}


void sBoxTransform(unsigned char* state) {
    for (int i = 0; i < 16; i++) {
        int lo = sBox[state[i] & 0xF];
        int hi = sBox[state[i] >> 4];
        state[i] = (hi << 4) | lo;
    }
}


void leftShiftBytes(unsigned char* state) {
    unsigned char temp[16];
    for (int i = 0; i < 16; i += 4) {
        temp[i + 0] = state[i + 2] >> 5 | (state[i + 1] << 3);
        temp[i + 1] = state[i + 3] >> 5 | (state[i + 2] << 3);
        temp[i + 2] = state[i + 0] >> 5 | (state[i + 3] << 3);
        temp[i + 3] = state[i + 1] >> 5 | (state[i + 0] << 3);
    }
    for (int i = 0; i < 16; i++)
    {
        state[i] = temp[i];
    }
}


// 轮密钥加
void addRoundKey(unsigned char* state, unsigned char* roundKey, unsigned int round) {
    for (int i = 0; i < 16; i++) {
        for (int j = 0; j < 8; j++) {
            state[i] ^= ((roundKey[i + round * 16] >> j) & 1) << j;
        }
    }
}

// 加密函数
void encrypt(unsigned char* password, unsigned int key, unsigned char* ciphertext) {
    unsigned char roundKeys[16 * ROUND] = {}; //

    // 生成轮密钥
    derive_round_key(key, roundKeys, 16 * ROUND);

    // 初始状态为16字节的口令
    unsigned char state[16]; // 初始状态为16字节的密码
    memcpy(state, password, 16); // 初始状态为密码的初始值

    // 迭代加密过程
    for (int round = 0; round < ROUND; round++)
    {
        reverseBits(state);
        sBoxTransform(state);
        leftShiftBytes(state);
        addRoundKey(state, roundKeys, round);
    }

    memcpy(ciphertext, state, 16);
}

void main() {
    unsigned char password[] = "pwd:xxxxxxxxxxxx"; // 口令明文固定以pwd:开头，16字节的口令
    unsigned int key = 0xF0FFFFFF; // 4字节的密钥
    unsigned char ciphertext[16]; // 16字节的状态

    printf("Password: \n");
    printf("%s\n", password);

    encrypt(password, key, ciphertext);

    // 输出加密后的结果
    printf("Encrypted password:\n");
    for (int i = 0; i < 16; i++) {
        printf("%02X", ciphertext[i]);
    }
    printf("\n");
}

题目基于一个对称加密，给出了其具体实现步骤。连接靶机之后会给出密文，要求求出password，来解压带密码的协同签名源码文件压缩包，压缩包内含有本题的flag值以及flag2的源码。

可以看出在有key的情况下，解密就是把整个加密过程逆一下，这一部分交给学长很快就写好了。

然而学长发现对于靶机给出的密文，用题目给定的0xF0FFFFFF当作key是解不出他要求的”pwd:”开头的password的，所以我猜测这个key只是个示例，实际上要用这个已知的开头来爆破4字节的key。4字节对于c来说似乎也不算很大，因此简单修改下解密部分就开爆了。但是，实际效果并不是很理想，如果要爆破完所有解空间的话，差不多需要2^16秒，这对于仅仅6h的比赛来说太长了，所以要考虑一些优化。而比起仔细查看代码来说，最简单的优化当然是直接用多进程来做。

可是我只用过python的多进程，并且考虑到python本身的速度，为了用个多进程把整个求解代码转成python实在是不太划算。可是比赛不出网，要查询资料不仅需要申请，时间也只限10min，还会对整个队伍的成绩产生影响，更不划算。所以想来想去也只能三个人都多开点窗口，然后从不同的位置开爆。

也算是一种多进程了。

然而这样做有意想不到的效果——我让学弟倒着爆破的那个窗口过了一段时间真的跑出了结果，这个题也就顺利解掉了。

实际上最后一轮提示中有提到，因为某些原因，key首字节一定是F，所以倒着爆才更加快；此外还有一些其他地方可以减少耗时。
这里就不仔细研究产生这些优化的原因了，多进程肯定是最有力的XD，做出来就行。

exp：(header.h就是题目加密源码里的函数)

#include "header.h"

void print(unsigned char* m) {
    for (int i = 0; i < 16; i++) {
        printf("%02X", m[i]); 
    }
    printf("\n"); 
}

int sBox_inv[16] =
{
    13, 4, 0, 5, 2, 12, 11, 8, 10, 6, 1, 9, 3, 15, 7, 14
}; 

void rightShiftBytes(unsigned char* state) {
    unsigned char temp[16]; 
    for (int i = 0; i < 16; i += 4) {
        temp[i + 0] = state[i + 2] << 5 | (state[i + 3] >> 3); 
        temp[i + 1] = state[i + 3] << 5 | (state[i + 0] >> 3); 
        temp[i + 2] = state[i + 0] << 5 | (state[i + 1] >> 3); 
        temp[i + 3] = state[i + 1] << 5 | (state[i + 2] >> 3); 
    }
    for (int i = 0; i < 16; i++) {
        state[i] = temp[i]; 
    }
}

void decrypt(unsigned char* password, unsigned int key, unsigned char* ciphertext) {
    unsigned char roundKeys[16 * ROUND] = {}; 
    derive_round_key(key, roundKeys, 16 * ROUND); 
    unsigned char state[16]; 
    memcpy(state, ciphertext, 16); 
    for (int round = ROUND - 1; round >= 0; round--) {
        addRoundKey(state, roundKeys, round);
        rightShiftBytes(state);
        sBoxTransform(state, sBox_inv);
        reverseBits(state);
    }
    memcpy(password, state, 16); 
}

int main() {
    // cipher = "B17164A27E035012107D6F7B0454D51D"
    // cipher = "99F2980AAB4BE8640D8F322147CBA409"

    unsigned char password[] = "pwd:xxxxxxxxxxxx"; // 口令明文固定以pwd:开头，16字节的口令
    unsigned char ciphertext[16]; // 16字节的状态
    hex_to_bytes("99F2980AAB4BE8640D8F322147CBA409", ciphertext, 16); 



    for (unsigned int key = 0; key < 0xFFFFFFFF; key++) {
        if ((key & 0xFFFF) == 0) printf("%d\n", key); 
        decrypt(password, key, ciphertext); 
        if (password[0] == 112 && password[1] == 119 && password[2] == 100 && password[3] == 58) {
            print(password); 
        }
    }

    return 0; 
}

flag2(900 pts)

题目：

co-signing_client.js：

const form = ref({
    password: "",
    msgdigest: "",
})

const k1: any = ref("");

const submit = () => {
    isform.value.validate((valid: boolean) => {
        if (valid) {
            
            loading.value = true;
            let smPassword = ref("");
            smPassword.value = sm3(form.value.password);
            // 客户端通过用户口令、消息摘要和用户私钥d1，计算客户端协同签名值 p1x, p1y, q1x, q1y, r1, s1
            var { str_e, str_p1x, str_p1y, str_q1x, str_q1y, str_r1, str_s1, errMessage } = clientSign1(smPassword.value, form.value.msgdigest);
            if (errMessage) {
                ElMessage.error(errMessage)
                loading.value = false;
                return
            }
            let data = {
                q1x: str_q1x,
                q1y: str_q1y,
                e: str_e,
                r1: str_r1,
                s1: str_s1,
                p1x: str_p1x,
                p1y: str_p1y
            }
            // 客户端将 e, p1x, p1y, q1x, q1y, r1, s1发送给服务端
            // 服务端用服务端私钥d2计算服务端协同签名值 s2, s3, r 发送给客户端
            sign_param_send(data).then((res: any) => {
                // 客户端通过s2, s3, r，计算协同签名值 s
                let str_s: any = clientSign2(smPassword.value, res.s2, res.s3, res.r);
                if (str_s.errMessage) {
                    ElMessage.error(errMessage)
                    loading.value = false;
                    return
                }
                ElMessage.success("协同签名成功");
                signature_send({ client_sign: str_s }).then((res: any) => {
                    qmz.value = str_s;
                    loading.value = false;
                }).then((err: any) => {
                    loading.value = false;
                })
            }).catch((err: any) => {
                loading.value = false;
            })
        }
    })
}
const clientSign1: any = (str_d1: any, str_e: any) => {
    let d1 = new BN(str_d1, 16);
    // console.log("e",str_e)
    
    let e = new BN(str_e, 16);
    // console.log("e",e)
    const sm2: any = new elliptic.curve.short({
        p: 'FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF',
        a: 'FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC',
        b: '28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93',
        n: 'FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123',
        g: [
            '32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7',
            'BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0'
        ]
    } as any);

    let n = new BN(sm2.n.toString(16), 16);    
    let G = sm2.g;

    // generate random k1
    const randomBytes = cryptoRandomStringAsync({ length: 64 });
    k1.value = new BN(randomBytes as any, 16);
    while(k1.value.mod(n).isZero()){
        const randomBytes = cryptoRandomStringAsync({ length: 64 });
        k1.value = new BN(randomBytes as any, 16);     
    }
    k1.value = k1.value.mod(n);

    // d1 = d1 mod n
    d1 = d1.mod(n);
    if (d1.isZero()) {
        let errMessage = "d1=0，签名失败"
        return { errMessage }
    }

    //P1 = ((d1)^(-1)) * G
    let tmp1 = d1.invm(n);
    let P1 = G.mul(tmp1);

    //Q1 = k1*G = (x, y)
    let Q1 = G.mul(k1.value);
    let x = new BN(Q1.getX().toString(16), 16);

    //r1 = x mod n
    let r1 = x.mod(n);
    if (r1.isZero()) {
        let errMessage = "r1=0，签名失败"
        return { errMessage }
    }

    //s1 = k1^(-1) * (e + d1^(-1) * r1) mod n
    tmp1 = d1.invm(n);
    let tmp2 = tmp1.mul(r1).mod(n);
    let tmp3 = tmp2.add(e).mod(n);
    tmp1 = k1.value.invm(n);
    let s1 = tmp1.mul(tmp3).mod(n);
    if (s1.isZero()) {
        let errMessage = "s1=0，签名失败"
        return { errMessage }
    }

    str_e = e.toString(16);
    // console.log("str_e",str_e)
    let str_p1x = P1.getX().toString(16);
    let str_p1y = P1.getY().toString(16);
    let str_q1x = Q1.getX().toString(16);
    let str_q1y = Q1.getY().toString(16);
    let str_r1 = r1.toString(16);
    let str_s1 = s1.toString(16);
    return { str_e, str_p1x, str_p1y, str_q1x, str_q1y, str_r1, str_s1 }
}
const clientSign2 = (str_d1: any, str_s2: any, str_s3: any, str_r: any) => {
    const sm2 = new elliptic.curve.short({
        p: 'FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF',
        a: 'FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC',
        b: '28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93',
        n: 'FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123',
        g: [
            '32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7',
            'BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0'
        ]
    } as any);

    let d1 = new BN(str_d1, 16);
    let n = new BN(sm2.n.toString(16), 16);
    let s2 = new BN(str_s2, 16);
    let s3 = new BN(str_s3, 16);
    let r = new BN(str_r, 16);
    //s = d1*k1*s2 + d1*s3 -r mod n
    let tmp1 = d1.mul(k1.value).mod(n);
    let tmp2 = tmp1.mul(s2).mod(n);
    let tmp3 = d1.mul(s3).mod(n);
    tmp1 = tmp2.add(tmp3).mod(n);
    let s = tmp1.sub(r).mod(n);
    if (s.isZero()) {
        let errMessage = "s=0，签名失败"
        return { errMessage }
    }
    if (s.add(r).mod(n).isZero()) {
        let errMessage = "s=n-r，签名失败"
        return { errMessage }
    }
    let str_s = s.toString(16);
    if (str_s[0] == '-') {
        s = s.add(n).mod(n);
        str_s = s.toString(16);
    }
    return str_s;
}

co-signing_client.c：

#include <stdio.h>
#include <stdlib.h>
#include <openssl/ec.h>
#include <openssl/rand.h>

#define SM2LEN 32

int error() {
    printf("Error.\n");
    return 0;
}

int error_partial_verify() {
    printf("Error partial verify.\n");
    return 0;
}

void print_flag2(const BIGNUM *d2) {
    char *hex_str = BN_bn2hex(d2);
    for (int i = 0; hex_str[i] != '\0'; i++) {
        if (hex_str[i] >= 'A' && hex_str[i] <= 'F') {
            hex_str[i] += 32;
        }
    }
    printf("flag2{%s}\n", hex_str);
}

typedef struct {
    char s2[SM2LEN * 2 + 1];
    char s3[SM2LEN * 2 + 1];
    char r[SM2LEN * 2 + 1];
    int success;
} Result;

// 协同签名服务端签名算法
Result server(char* str_e,char* str_p1x,char* str_p1y,char* str_q1x,char* str_q1y,char* str_r1,char* str_s1){
    Result res = {"", "", "", 0};

	int rv = 1;
	BIGNUM *e,*a,*b,*p,*n,*x,*y;
	BIGNUM *d2,*r1,*s1,*p1x,*p1y,*q1x,*q1y;
	BIGNUM *u1,*u2,*xprime,*yprime,*k2,*k3,*x1,*y1,*r,*s2,*s3,*s,*tmp1,*tmp2,*tmp3;
	EC_GROUP* group;
	EC_POINT *generator,*G,*P,*P1,*Q1,*TMP;

	BN_CTX* bn_ctx = BN_CTX_new();
	BN_CTX_start(bn_ctx);
	if (!bn_ctx)
		{ error(); return res; }
	e = BN_CTX_get(bn_ctx);
	a = BN_CTX_get(bn_ctx);
	b = BN_CTX_get(bn_ctx);
	p = BN_CTX_get(bn_ctx);
	n = BN_CTX_get(bn_ctx);
	d2 = BN_CTX_get(bn_ctx);
	x = BN_CTX_get(bn_ctx);
	y = BN_CTX_get(bn_ctx);
	p1x = BN_CTX_get(bn_ctx);
	p1y = BN_CTX_get(bn_ctx);
	q1x = BN_CTX_get(bn_ctx);
	q1y = BN_CTX_get(bn_ctx);
	r1 = BN_CTX_get(bn_ctx);
	s1 = BN_CTX_get(bn_ctx);
	u1 = BN_CTX_get(bn_ctx);
	u2 = BN_CTX_get(bn_ctx);
	xprime = BN_CTX_get(bn_ctx);
	yprime = BN_CTX_get(bn_ctx);
	k2 = BN_CTX_get(bn_ctx);
	k3 = BN_CTX_get(bn_ctx);
	x1 = BN_CTX_get(bn_ctx);
	y1 = BN_CTX_get(bn_ctx);
	r = BN_CTX_get(bn_ctx);
	s2 = BN_CTX_get(bn_ctx);
	s3 = BN_CTX_get(bn_ctx);
	s = BN_CTX_get(bn_ctx);
	tmp1 = BN_CTX_get(bn_ctx);
	tmp2 = BN_CTX_get(bn_ctx);
	tmp3 = BN_CTX_get(bn_ctx);

	if (
		!BN_hex2bn(&e, str_e) ||
		!BN_hex2bn(&p1x, str_p1x) ||
		!BN_hex2bn(&p1y, str_p1y) ||
		!BN_hex2bn(&q1x, str_q1x) ||
		!BN_hex2bn(&q1y, str_q1y) ||
		!BN_hex2bn(&r1, str_r1) ||
		!BN_hex2bn(&s1, str_s1) ||
		!BN_hex2bn(&a, "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC") ||
		!BN_hex2bn(&b, "28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93") ||
		!BN_hex2bn(&p, "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF") ||
		!BN_hex2bn(&n, "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123") ||
		// d2 = ds (server key)
		!BN_hex2bn(&d2, "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX") ||
		!BN_hex2bn(&x, "32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7") ||
		!BN_hex2bn(&y, "BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0") ||
		!BN_rand_range(k2,n) ||
		!BN_copy(k3, k2)
		)
		{ error(); return res; }

    // generate k2 in [1, n-1]
	while(BN_is_zero(k2)){
        if (
            !BN_rand_range(k2,n) ||
            !BN_copy(k3, k2)
            )
            { error(); return res; }
	}

	group = EC_GROUP_new_curve_GFp(p, a, b, bn_ctx);
	generator = EC_POINT_new(group);
	if (!generator)
		{ error(); return res; }
	if (1 != EC_POINT_set_affine_coordinates_GFp(group, generator, x, y, bn_ctx))
		{ error(); return res; }
	if (1 != EC_GROUP_set_generator(group, generator, n, NULL))
		{ error(); return res; }

	G = EC_POINT_new(group);
	P = EC_POINT_new(group);
	P1 = EC_POINT_new(group);
	Q1 = EC_POINT_new(group);
	TMP = EC_POINT_new(group);

    // if r1=0 or s1=0, error
	if (BN_is_zero(r1) || BN_is_zero(s1))
		{ error(); return res; }

	// set P1 = (p1x, p1y)
	if (1 != EC_POINT_set_affine_coordinates_GFp(group, P1, p1x, p1y, bn_ctx))
		{ error(); return res; }

	// set Q1 = (q1x, q1y)
	if (1 != EC_POINT_set_affine_coordinates_GFp(group, Q1, q1x, q1y, bn_ctx))
		{ error(); return res; }

	//u1 = e * (s1^(-1)) mod n, u2 = r1 * (s1^(-1)) mod n
	if (!BN_mod_inverse(tmp1, s1, n, bn_ctx) ||
		!BN_mod_mul(u1, e, tmp1, n, bn_ctx) ||
		!BN_mod_mul(u2, r1, tmp1, n, bn_ctx) ||
		!BN_mod(u1, u1, n, bn_ctx) ||
		!BN_mod(u2, u2, n, bn_ctx)
		)
		{ error(); return res; }

	//u1*G + u2*P1 = (x', y')
	if (!EC_POINT_mul(group, TMP, u1, P1, u2, bn_ctx))
		{ error(); return res; }

	if (!EC_POINT_get_affine_coordinates_GFp(group, TMP, xprime, yprime, bn_ctx))
		{ error(); return res; }

	//verify r1 = x' mod n
	if (!BN_mod(xprime, xprime, n, bn_ctx))
		{ error(); return res; }

	if(BN_cmp(r1,xprime))
		{ error_partial_verify(); return res; }

	//k2*G + k3*Q1 = (x1, y1)
	if (!EC_POINT_mul(group, TMP, k2, Q1, k3, bn_ctx))
		{ error(); return res; }

	if (!EC_POINT_get_affine_coordinates_GFp(group, TMP, x1, y1, bn_ctx))
		{ error(); return res; }

	//r=(e+x1) mod n
	if (!BN_mod_add(r, e, x1, n, bn_ctx))
		{ error(); return res; }

	if (BN_is_zero(r))
		{ error(); return res; }
	strncpy(res.r, BN_bn2hex(r), 2*SM2LEN+1);

	//s2 = d2 * k3 mod n, s3 = d2 * (r+k2) mod n
	if (!BN_mod_mul(s2, d2, k3, n, bn_ctx) ||
		!BN_mod_add(tmp1, r, k2, n, bn_ctx) ||
		!BN_mod_mul(s3, d2, tmp1, n, bn_ctx) ||
		!BN_mod(s2, s2, n, bn_ctx) ||
		!BN_mod(s3, s3, n, bn_ctx)
		)
		{ error(); return res; }
	printf("s2: %s\n",BN_bn2hex(s2));
	printf("s3: %s\n",BN_bn2hex(s3));
	strncpy(res.s2, BN_bn2hex(s2), 2*SM2LEN+1);
	strncpy(res.s3, BN_bn2hex(s3), 2*SM2LEN+1);

    // flag2 的格式如下：flag2{xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx}，大括号中的内容为 16 进制格式（字母小写）的 d2。
    print_flag2(d2);

    rv = 0;
    BN_CTX_free(bn_ctx);

    return rv;
}

// 计算公钥P
int getPublicKey(char *str_d2, char *str_p1x, char *str_p1y) {
    int rv = 1;
    BIGNUM *negone, *a, *b, *p, *n, *x, *y;
    BIGNUM *d2, *p1x, *p1y, *px, *py;
    BIGNUM *tmp1, *tmp2;
    EC_GROUP *group;
    EC_POINT *generator, *G, *P, *P1;

    BN_CTX *bn_ctx = BN_CTX_new();
    BN_CTX_start(bn_ctx);
    if (!bn_ctx) {
        error();
        return 1;
    }

    negone = BN_CTX_get(bn_ctx);
    a = BN_CTX_get(bn_ctx);
    b = BN_CTX_get(bn_ctx);
    p = BN_CTX_get(bn_ctx);
    n = BN_CTX_get(bn_ctx);
    d2 = BN_CTX_get(bn_ctx);
    x = BN_CTX_get(bn_ctx);
    y = BN_CTX_get(bn_ctx);
    p1x = BN_CTX_get(bn_ctx);
    p1y = BN_CTX_get(bn_ctx);
    px = BN_CTX_get(bn_ctx);
    py = BN_CTX_get(bn_ctx);
    tmp1 = BN_CTX_get(bn_ctx);
    tmp2 = BN_CTX_get(bn_ctx);

    if (
        !BN_hex2bn(&d2, str_d2) ||
        !BN_hex2bn(&p1x, str_p1x) ||
        !BN_hex2bn(&p1y, str_p1y) ||
        !BN_hex2bn(&a, "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC") ||
        !BN_hex2bn(&b, "28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93") ||
        !BN_hex2bn(&p, "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF") ||
        !BN_hex2bn(&n, "FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123") ||
        !BN_hex2bn(&x, "32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7") ||
        !BN_hex2bn(&y, "BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0")
    ) {
        error();
        return 1;
    }
    group = EC_GROUP_new_curve_GFp(p, a, b, bn_ctx);
    generator = EC_POINT_new(group);
    if (!generator) {
        error();
        return 1;
    }
    if (1 != EC_POINT_set_affine_coordinates_GFp(group, generator, x, y, bn_ctx)) {
        error();
        return 1;
    }
    if (1 != EC_GROUP_set_generator(group, generator, n, NULL)) {
        error();
        return 1;
    }

    G = EC_POINT_new(group);
    P = EC_POINT_new(group);
    P1 = EC_POINT_new(group);

    // set P1 = (p1x, p1y)
    if (1 != EC_POINT_set_affine_coordinates_GFp(group, P1, p1x, p1y, bn_ctx)) {
        error();
        return 1;
    }

    //P = ((d2)^(-1)) * P1 - G
    if (!BN_zero(tmp1) ||
        !BN_one(tmp2) ||
        !BN_mod_sub(negone, tmp1, tmp2, n, bn_ctx)
    ) {
        error();
        return 1;
    }
    if (!BN_mod_inverse(tmp1, d2, n, bn_ctx) || !EC_POINT_mul(group, P, negone, P1, tmp1, bn_ctx)) {
        error();
        return 1;
    }

    if (!EC_POINT_get_affine_coordinates_GFp(group, P, px, py, bn_ctx)) {
        error();
        return 1;
    }
    printf("Px: %s\n", BN_bn2hex(px));
    printf("Py: %s\n", BN_bn2hex(py));

    rv = 0;
    BN_CTX_free(bn_ctx);

    return rv;
}

int main(int argc, char *argv[]) {
    int rv = 1;
    if (server(argv[1], argv[2], argv[3], argv[4], argv[5], argv[6], argv[7])) {
        error();
        return rv;
    }

    rv = 0;
    return rv;
}

这个题目代码特别特别的长，具体细节可以慢慢读。

.js文件是交互部分，梳理一下主要交互流程是：

用户输入口令和消息摘要，并发送给服务器

用户本地计算出如下数据，这些数据可以在发送包的负载里找到：

e, p1x, p1y, q1x, q1y, r1, s1

服务器接收到数据后，进行协同签名，并发送以下数据返回：

   s2, s3, r

我们需要计算出服务器的私钥d2，d2就是flag2的值

而.c文件则是告诉我们协同签名流程，这些数据主要有以下一些关系(运算均在模n下，n是曲线阶)：

使用SM2的标准曲线，参数及生成元G均已知，服务器私钥为d2，并有以下P点坐标：

使用用户发送来的p1x, p1y, q1x, q1y这几个数据设置点P1、Q1

使用用户发送来的e、r1、s1计算u1、u2：

计算中间点T(x’,y’)，验证r1=x’：

生成随机数k2、k3，并计算：

计算r：

计算s2、s3：

返回r、s2、s3

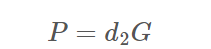
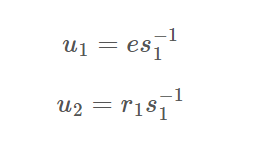
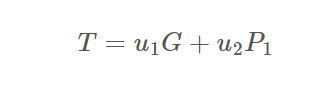
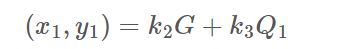
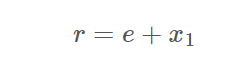
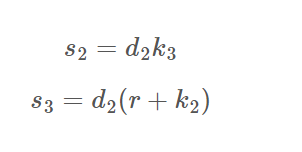
整个步骤就是看注释一步步梳理出来的，我们的目的是算出d2来，而s2、s3中一共有三个变量d2、k2、k3，并不足以求出所有未知数，所以可能需要利用r再构造一个等式才行。

然而这个题藏了个相当阴的地方，仔细观察可以发现一行代码：

BN_copy(k3, k2)

这也就是说k3=k2，因此未知数实际上就只有两个，所以很轻松就可以拿到d2了XD。

exp：

from Crypto.Util.number import *

a = int("FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC", 16)
b = int("28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93", 16)
p = int("FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF", 16)
n = int("FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123", 16)
x = int("32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7", 16)
y = int("BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0", 16)

E = EllipticCurve(Zmod(p),[a,b])
G = E(x,y)


################################################################################# res
e = "ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff"
p1x = "3e8eda67c5f1b70ac1950f615c2c4e0b0fe2544823ac96cb127ba318d96b4f5"
p1y = "ab1bbde72e7d1ef42e0c9d18d44a10e7250a0dfea98194f2d8d591b355fc636"
q1x = "bc44ec67a42c1613d9cf99f7bd2d1d859ab94823ba6cfb1836e8083e23bbd41e"
q1y = "faef1f853c095d6de79ba9ad9a2026d742042116b38b1c672ae67c7c7e9e762d"
r1 = "bc44ec67a42c1613d9cf99f7bd2d1d859ab94823ba6cfb1836e8083e23bbd41e"
s1 = "6c1bfef8bacf4f9c8bc4703c66458715475e50d17ba84f666372b4f4c364e16f"
r = "C987C22813DD2D0537433FF583C84B047E0313DCA072E187ACBB5A638D4E2BC0"
s2 = "E1E08110628EEB528DC26AA117AFEF8613B1D22EBFD77A9F42524CEFEB57F676"
s3 = "758CBCCFADFB5078DB26DF382A179C9AFDE1D0617D92EC5496F67380162235B6"

tt = [e,p1x,p1y,q1x,q1y,r1,s1,r,s2,s3]
e,p1x,p1y,q1x,q1y,r1,s1,r,s2,s3 = [int(i,16) for i in tt]
P1 = E(p1x,p1y)
Q1 = E(q1x,q1y)
u1 = e * inverse(s1, n) % n
u2 = r1 * inverse(s1, n) % n
T = u1*G + u2*P1
x_, y_ = T.xy()
assert r1 == x_
x1 = r - e

d2 = (s3-s2)*inverse(r,n) % n
print(hex(d2))

#flag2{a61bdbacbad62b141284a6955b14a27df01c09984e23785ec75b5e5c79e18f62}

flag3(500 pts)

题目：

package controllers

import (
	"crypto/ecdsa"
	"encoding/hex"
	"encoding/pem"
	"fmt"
	jwtgo "github.com/dgrijalva/jwt-go"
	"github.com/gin-gonic/gin"
	"github.com/tjfoc/gmsm/sm2"
	"github.com/tjfoc/gmsm/x509"
	"http_svr/config"
	"http_svr/models"
	"http_svr/utils"
	"math/big"
	"net/http"
	"time"
)

// 加载证书
func loadCertificate(certPEM string) (*x509.Certificate, error) {
	//certPEM := "-----BEGIN CERTIFICATE-----\nMIIBQDCB6KADAgECAgECMAoGCCqBHM9VAYN1MBIxEDAOBgNVBAoTB1Jvb3QgQ0Ew\nHhcNMjQwNzI0MDkyMTI5WhcNMjUwNzI0MDkyMTI5WjAaMRgwFgYDVQQKEw9NeSBP\ncmdhbml6YXRpb24wWTATBgcqhkjOPQIBBggqgRzPVQGCLQNCAASlPepwTvt5c4rF\nEsg1Mqs+Tyx/BwRkwyWqDyZd/gBFKp7veuoZnGK11c24xPOqR/eQZNW7ugsZW6eb\nLyXSsE9ooycwJTAOBgNVHQ8BAf8EBAMCBaAwEwYDVR0lBAwwCgYIKwYBBQUHAwEw\nCgYIKoEcz1UBg3UDRwAwRAIgG4/snkgUCW819OotUWUfMOo0BzHX8KeTTUSLpIjy\nEO4CIEq6X7h3nVNeFzdtLWdy5+1MeNwsWawHU5YzITsNtqOe\n-----END CERTIFICATE-----\n"
	block, _ := pem.Decode([]byte(certPEM))
	if block == nil || block.Type != "CERTIFICATE" {
		return nil, fmt.Errorf("无效的证书格式")
	}

	return x509.ParseCertificate(block.Bytes)
}

// 验证证书
func validateCertificate(cert *x509.Certificate, rootCert *x509.Certificate) error {
	// 检查颁发者
	if cert.Issuer.CommonName != rootCert.Subject.CommonName {
		return fmt.Errorf("证书校验失败")
	}
	// 检查颁发者组织
	if len(cert.Issuer.Organization) != 1 || cert.Issuer.Organization[0] != rootCert.Subject.Organization[0] {
		return fmt.Errorf("证书校验失败")
	}
	// 检查颁发者国家
	if len(cert.Issuer.Country) != 1 || cert.Issuer.Country[0] != rootCert.Subject.Country[0] {
		return fmt.Errorf("证书校验失败")
	}

	// 检查有效日期
	if time.Now().Before(cert.NotBefore) || time.Now().After(cert.NotAfter) {
		return fmt.Errorf("证书校验失败")
	}

	// 检查组织
	if len(cert.Subject.Organization) != 1 || cert.Subject.Organization[0] != "ShangMiBei" {
		return fmt.Errorf("证书校验失败")
	}

	// 检查组织单元
	if len(cert.Subject.OrganizationalUnit) != 1 || cert.Subject.OrganizationalUnit[0] != "ShangMiBei2024" {
		return fmt.Errorf("证书校验失败")
	}

	// 检查国家
	if len(cert.Subject.Country) != 1 || cert.Subject.Country[0] != "CN" {
		return fmt.Errorf("证书校验失败")
	}

	// 创建证书链
	roots := x509.NewCertPool()
	roots.AddCert(rootCert)

	opts := x509.VerifyOptions{
		Roots:       roots,
		CurrentTime: time.Now(),
	}

	// 验证证书链
	if _, err := cert.Verify(opts); err != nil {
		return fmt.Errorf("证书链校验失败: %v", err)
	}

	return nil
}

type SM2Signature struct {
	R, S *big.Int
}

// 验证签名
func validateSignature(message, signature string, publicKey *sm2.PublicKey) (bool, error) {
	//rawSignatureHex, err := base64.StdEncoding.DecodeString(base64EncodedSignature)
	hexSignature, err := hex.DecodeString(signature)
	if err != nil {
		return false, fmt.Errorf("invalid signature format")
	}

	isValid := publicKey.Verify([]byte(message), hexSignature)
	if isValid {
		return true, nil
	} else {
		return false, fmt.Errorf("signature is invalid")
	}
}

// Login 登录
func Login(c *gin.Context, conf config.Config) {
	// 解析请求参数
	var req models.LoginReq
	if err := c.ShouldBind(&req); err != nil {
		c.JSON(http.StatusBadRequest, gin.H{"error": err.Error()})
		return
	}

	// 校验用户名是否已注册过
	if _, exists := models.Users[req.Username]; !exists {
		c.JSON(http.StatusBadRequest, gin.H{"error": "username not exists"})
		return
	}

	// 校验随机字符串是否过期
	randomStr, exists := conf.Cache.Get(req.Username)
	if !exists {
		c.JSON(http.StatusBadRequest, gin.H{"error": "random string has expired"})
		return
	}

	// 校验证书
	cert, err := loadCertificate(req.Cert)
	if err != nil {
		c.JSON(http.StatusBadRequest, gin.H{"error": err.Error()})
		return
	}
	if err := validateCertificate(cert, models.RootCert); err != nil {
		c.JSON(http.StatusBadRequest, gin.H{"error": err.Error()})
		return
	}

	// 判断是否挑战成功（随机字符串的签名能否用证书中的公钥验签过）
	ecdsaPubKey, ok := cert.PublicKey.(*ecdsa.PublicKey)
	if !ok {
		c.JSON(http.StatusBadRequest, gin.H{"error": "public key in cert is not sm2"})
		return
	}
	sm2PubKey := sm2.PublicKey{
		Curve: ecdsaPubKey.Curve,
		X:     ecdsaPubKey.X,
		Y:     ecdsaPubKey.Y,
	}
	isValid, err := validateSignature(randomStr.(string), req.Signature, &sm2PubKey)
	if isValid {
		//c.JSON(http.StatusOK, gin.H{"msg": "success", "flag3": config.Flag3, "download_url": config.DownloadUrl})
		generateToken2(c, req.Username, conf)
	} else {
		c.JSON(http.StatusBadRequest, gin.H{"error": err.Error()})
	}
}

// 生成令牌
func generateToken2(c *gin.Context, username string, conf config.Config) {
	j := &utils.JWT{
		SigningKey: []byte(conf.SignKey),
	}
	claims := utils.CustomClaims{
		Name: username,
		StandardClaims: jwtgo.StandardClaims{
			NotBefore: time.Now().Unix() - conf.NotBeforeTime, // 签名生效时间
			ExpiresAt: time.Now().Unix() + conf.ExpiresTime,   // 过期时间
			Issuer:    conf.Issuer,                            // 签名的发行者
		},
	}

	token, err := j.CreateToken(claims)
	if err != nil {
		c.JSON(http.StatusOK, gin.H{
			"code": 5091,
			"msg":  "登录失败，系统有误",
		})
		return
	}

	// 将当前用户对应的缓存中的随机字符串删除
	conf.Cache.Delete(username)

	isAdmin := false
	if username == "shangmibeiadmin" {
		isAdmin = true
	}
	c.JSON(http.StatusOK, gin.H{
		"code":     0,
		"msg":      "登录成功",
		"token":    token,
		"is_admin": isAdmin,
	})
	return
}

数据库管理系统管理员证书.cer：

题目连接上之后有一个简易的网站，由于复现不了所以只能大致描述一下它的功能：

有一个登录界面，可以输入用户名、私钥以及公钥文件，如果能通过login.go中的所有check就能成功登录
还有一个注册界面，可以输入用户名和裸公钥，如果裸公钥格式正确，服务器就会用根证书发放一个完整公钥文件给你

我们的目标是用“shangmibeiadmin”成功登录，就可以拿到flag3的值以及flag4的源码。

已知的这个证书文件是个公钥文件，查看一下发现这个证书的用户就是“shangmibeiadmin”，所以如果我们能知道他的私钥的话就可以直接登录了。结合这个题只有500分这个事实，我第一反应是私钥相当小，可以直接爆出来，但是用mitm爆了2^50无果，所以只能从其他部分入手。

用gmssl这个工具可以比较轻松的生成一对公私钥证书，我们只需要把公钥里的裸公钥拆出来，然后自己随便生成个用户名就可以注册一个用户，并得到服务器颁发的公钥证书。

这里需要注意一下不能直接注册“shangmibeiadmin”，它会显示已注册

然后查看login.go可以发现他似乎根本没检验证书持有者是不是和用户名一样，所以按理来说接下来的步骤很简单，我们只需要在用户名一栏输入“shangmibeiadmin”，然后输入刚才我们生成的公私钥证书中的私钥，再输入刚才服务器下发的证书就可以成功登录。

然而我们实在是不熟悉gmssl乃至openssl这些工具，并且不出网，不能自由查找怎么使用，所以只能一直用help来看有什么参数可以用。我们遇到的最大问题是：gmssl必须要一个密码，才能生成sm2私钥文件，而这个私钥文件是用这个密码加密过的，但是我们怎么找都找不到怎么解密这个私钥文件并解析他。

这里花了很长很长时间，最后离比赛结束不到一小时的时候想了一个笨办法出来——直接去源码c文件里面加几行打印私钥d的文件，并重新编译一下再用这个工具：

这个方法很笨但是确实有效，由于脑子有点混乱，也想不太清楚d具体该怎么拼，就用从前往后和从后往前两种顺序得到两个d，并用是否满足P=dG这个式子来进行核验，最后好歹是把自己生成的私钥d搞出来了：

from Crypto.Util.number import *
from tqdm import *

a = int("FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC", 16)
b = int("28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93", 16)
p = int("FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF", 16)
n = int("FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123", 16)
x = int("32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7", 16)
y = int("BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0", 16)

E = EllipticCurve(Zmod(p),[a,b])
G = E(x,y)

t = "3059301306072a8648ce3d020106082a811ccf5501822d03420004ed7a7dce0e4e2e4b779f76b4ec407b8987ba5c3beba5cd454604e587fce0a17160b29510b2beb36e36470fba3ed6bd436049a0b588e931c71df6cf0b0d0e6407"
x1 = int(t[-128:-64], 16)
y1 = int(t[-64:], 16)

P = E(x1,y1)

dd = [12437958772606967559,9879664919779981675,172814172046494727,15816591967453487196]

d = (dd[3] << (64*3)) + (dd[2] << (64*2)) + (dd[1] << (64*1)) + (dd[0] << (64*0))
print(d)
print(hex(d))
print(d*G == P)

之后按刚才的方式就可以登录上网站拿到flag3以及flag4的源码。

flag4(1000 pts)

题目：

SM4加密解密代码.py：

from gmssl.sm4 import CryptSM4, SM4_ENCRYPT, SM4_DECRYPT

MULTIPLIER = 6364136223846793005
ADDEND = 1
MASK = 0xffffffffffffffff
ITERATIONS = 1000

# 从文件中读取seed
def read_seed(file_path):
    with open(file_path, 'r') as file:
        seed = int(file.read().strip(), 16)
        print("seed:", hex(seed))
    return seed

global_seed = read_seed('seed.txt')

def genRandom():
    global global_seed
    # print("global_seed", hex(global_seed))
    for _ in range(ITERATIONS):
        global_seed = (global_seed * MULTIPLIER + ADDEND) & MASK
    return (global_seed >> 32) & 0xffffffff

# 16进制字符串转bytes
def HexStringToBytes(hex_str):
    return bytes.fromhex(hex_str)

# bytes转16进制字符串
def BytesToHexString(byte_seq):
    return byte_seq.hex()

def genSM4KeyOrIV():
    return HexStringToBytes(''.join(f'{genRandom():08x}' for _ in range(4)))

def SM4Encrypt(data_bytes, key_bytes, iv_bytes):
    sm4 = CryptSM4()
    sm4.set_key(key_bytes, SM4_ENCRYPT)
    return sm4.crypt_cbc(iv_bytes, data_bytes)

def SM4Decrypt(cipher_bytes, key_bytes, iv_bytes):
    sm4 = CryptSM4()
    sm4.set_key(key_bytes, SM4_DECRYPT)
    return sm4.crypt_cbc(iv_bytes, cipher_bytes)


print("############ SM4 Cryptographic Services Start... ###################")

iv_bytes = genSM4KeyOrIV()
print("iv hex:", BytesToHexString(iv_bytes))

key_bytes = genSM4KeyOrIV()
print("key hex:", BytesToHexString(key_bytes))

# 从test.pcapng读取数据并加密
with open('test.pcapng', 'rb') as f1:
    plain1_bytes = f1.read()
    cipher1_bytes = SM4Encrypt(plain1_bytes,key_bytes,iv_bytes)

# 写密文数据到cipherText.dat
with open('cipherText.dat', 'wb') as f2:
    f2.write(cipher1_bytes)

# 从cipherText.dat读密文数据
with open('cipherText.dat', 'rb') as f3:
    cipher2_bytes = f3.read()
    plain2_bytes = SM4Decrypt(cipher2_bytes,key_bytes,iv_bytes)

# 解密密文并将明文写入到plainText.pcapng(含flag4)
with open('plainText.pcapng', 'wb') as f4:
    f4.write(plain2_bytes)

总经理协同签名流量包加密使用的iv.txt：

90fc5cf2e2f47488a257fd51e0ae615

终于是一个python加密了，倍感亲切。题目主要流程是：

读取seed.txt文件得到初始seed
用genSM4KeyOrIV函数连续生成16字节的iv和key
读取一个流量包文件，并用iv、key对流量包文件进行SM4加密
给出密文文件以及iv，要求还原流量包

有古怪的地方只可能在genSM4KeyOrIV函数里，查看一下发现其是连续调用四次genRandom函数并拼接而成，而genRandom函数是：

def genRandom():
    global global_seed
    # print("global_seed", hex(global_seed))
    for _ in range(ITERATIONS):
        global_seed = (global_seed * MULTIPLIER + ADDEND) & MASK
    return (global_seed >> 32) & 0xffffffff

可以看出这是一个LCG过程，其会返回seed迭代一千次之后的高32位。

我们知道IV，也就是我们知道连续四次迭代一千次之后的seed高位，这就变成了一个简单的HNP问题。由于LCG迭代过程可以写为如下矩阵乘法：

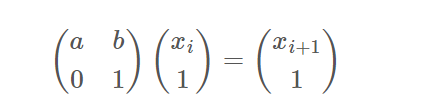
所以一千次迭代也就是：

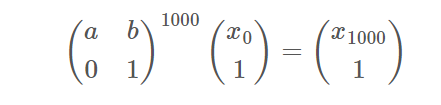
对于题目来说是已知高32位，那么以IV的第一个分组和第二个分组为例，式子就可以写成：

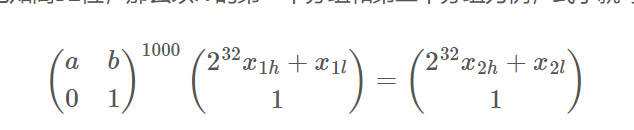
所以对IV所有连续的两组用第一行对应的线性等式，就可以把问题转化成规约低32位的HNP问题了，得到所有低位之后就可以向后迭代得到key，从而恢复流量包。

exp：

get xl：

c = "90fc5cf2e2f47488a257fd51e0ae615b"

MULTIPLIER = 6364136223846793005
ADDEND = 1
MASK = 0xffffffffffffffff + 1
ITERATIONS = 1000

t1,t2,t3,t4 = c[:8],c[8:16],c[16:24],c[24:32]
res = [t1,t2,t3,t4]
t = [int(i,16) for i in res]

################################################## 
M = Matrix(Zmod(MASK),[
    [MULTIPLIER,1],
    [0,1]
])
Mn = M^ITERATIONS
a,b = Mn[0]
a,b = int(a),int(b)

nums = 4
L = Matrix(ZZ,2*nums,2*nums)
for i in range(nums+1):
    L[i,i] = 1
for i in range(nums-1):
    L[i,nums+i+1] = a
    L[i+1,nums+i+1] = -1
    c = a*2^32*t[i] - 2^32*t[i+1] + b
    L[nums,nums+i+1] = c
L[nums,nums] = 2^32
for i in range(nums-1):
    L[-i-1,-i-1] = MASK
L[:,-(nums-1):] *= MASK

res = L.LLL()[0][:4]
print(res)

decrypt：

from gmssl.sm4 import CryptSM4, SM4_ENCRYPT, SM4_DECRYPT

MULTIPLIER = 6364136223846793005
ADDEND = 1
MASK = 0xffffffffffffffff
ITERATIONS = 1000

global_seed = 0 # TODO
iv_high = 0xe0ae615b
iv_low = 187714221
iv_last = (iv_high << 32) + iv_low
global_seed = iv_last

def genRandom():
    global global_seed
    # print("global_seed", hex(global_seed))
    for _ in range(ITERATIONS):
        global_seed = (global_seed * MULTIPLIER + ADDEND) & MASK
    return (global_seed >> 32) & 0xffffffff

# 16进制字符串转bytes
def HexStringToBytes(hex_str):
    return bytes.fromhex(hex_str)

# bytes转16进制字符串
def BytesToHexString(byte_seq):
    return byte_seq.hex()

def genSM4KeyOrIV():
    return HexStringToBytes(''.join(f'{genRandom():08x}' for _ in range(4)))

def SM4Encrypt(data_bytes, key_bytes, iv_bytes):
    sm4 = CryptSM4()
    sm4.set_key(key_bytes, SM4_ENCRYPT)
    return sm4.crypt_cbc(iv_bytes, data_bytes)

def SM4Decrypt(cipher_bytes, key_bytes, iv_bytes):
    sm4 = CryptSM4()
    sm4.set_key(key_bytes, SM4_DECRYPT)
    return sm4.crypt_cbc(iv_bytes, cipher_bytes)

iv_bytes = HexStringToBytes("90fc5cf2e2f47488a257fd51e0ae615b")
key_bytes = genSM4KeyOrIV()
print(key_bytes)

with open("总经理协同签名流量包（加密后的文件）.dat", "rb") as fp:
    cipher_bytes = fp.read()
    plain_bytes = SM4Decrypt(cipher_bytes, key_bytes, iv_bytes)

with open("plainText.pcapng", "wb") as fp:
    fp.write(plain_bytes)

然后就可以在流量包里找到flag4。

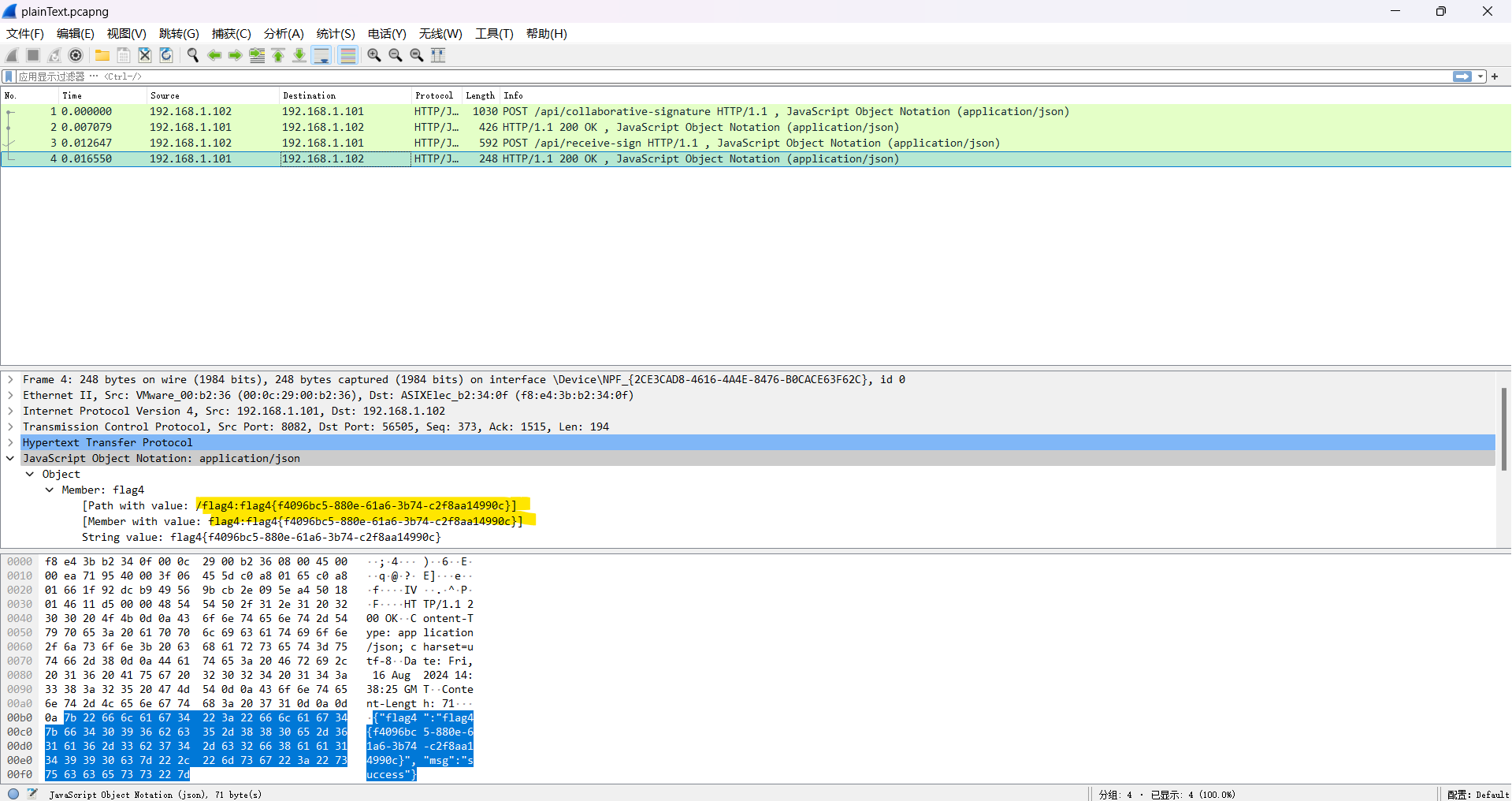
最终挑战 *

在比赛还是不到半分钟的时候，我们队才惊险地交上flag4，完全没有时间看最终挑战了，因此只能赛后复现一下。

flag4的流量包跟踪TCP流，可以看到里面有以下内容：

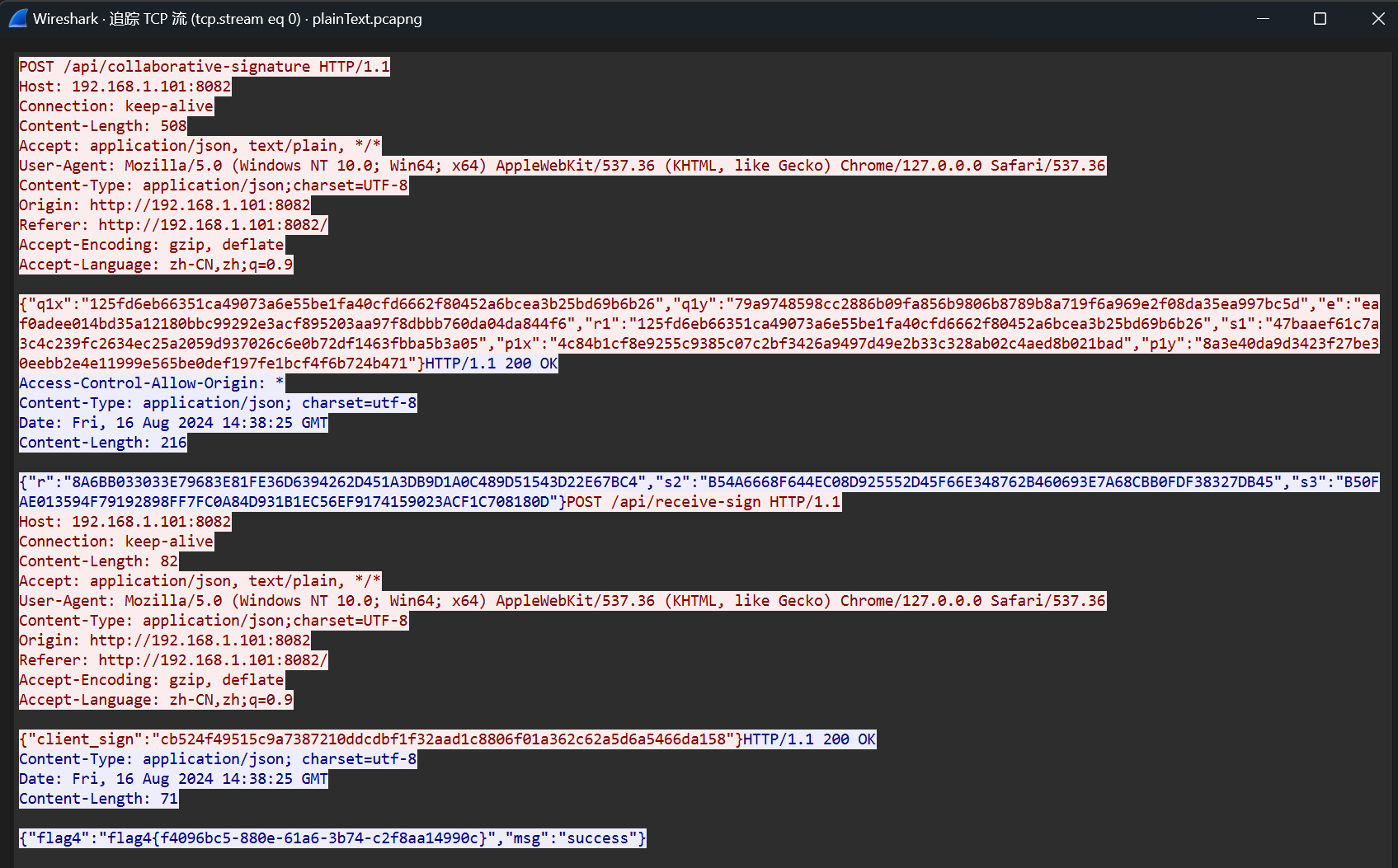
除了flag4外，剩下的数据很显然是和flag2的协同签名有关的，而相比于flag2来说，这里多给了一个client_sign字段的值，再回头看看.js文件可以发现这是clientSign2函数的返回值，其流程为：

在clientSign1的过程里会生成一个随机数k1，满足：

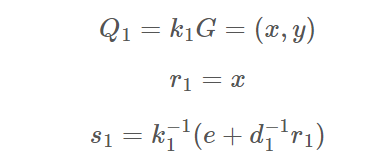
传入未知的用户私钥d1，以及已知的s2、s3、r

计算s：

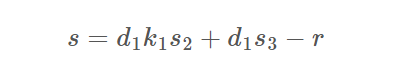
可以看出s1、s的生成等式其实分别就是关于d1、k1的两个变量的方程，所以就可以解出d1了。而我们的目的是伪造一个签名，解出d1之后走一遍协同签名的流程就好了，自然也就没有难度。

没有交互部分了，但可以用d1联系的两个点来检验d1的正确性

exp：

from Crypto.Util.number import *

a = int("FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC", 16)
b = int("28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93", 16)
p = int("FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF", 16)
n = int("FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123", 16)
x = int("32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7", 16)
y = int("BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0", 16)

E = EllipticCurve(Zmod(p),[a,b])
G = E(x,y)


################################################################################# res
q1x = "125fd6eb66351ca49073a6e55be1fa40cfd6662f80452a6bcea3b25bd69b6b26"
q1y = "79a9748598cc2886b09fa856b9806b8789b8a719f6a969e2f08da35ea997bc5d"
e = "eaf0adee014bd35a12180bbc99292e3acf895203aa97f8dbbb760da04da844f6"
r1 = "125fd6eb66351ca49073a6e55be1fa40cfd6662f80452a6bcea3b25bd69b6b26"
s1 = "47baaef61c7a3c4c239fc2634ec25a2059d937026c6e0b72df1463fbba5b3a05"
p1x = "4c84b1cf8e9255c9385c07c2bf3426a9497d49e2b33c328ab02c4aed8b021bad"
p1y = "8a3e40da9d3423f27be30eebb2e4e11999e565be0def197fe1bcf4f6b724b471"

r = "8A6BB033033E79683E81FE36D6394262D451A3DB9D1A0C489D51543D22E67BC4"
s2 = "B54A6668F644EC08D925552D45F66E348762B460693E7A68CBB0FDF38327DB45"
s3 = "B50FAE013594F79192898FF7FC0A84D931B1EC56EF9174159023ACF1C708180D"

s = "cb524f49515c9a7387210ddcdbf1f32aad1c8806f01a362c62a5d6a5466da158"


tt = [e,p1x,p1y,q1x,q1y,r1,s1,r,s2,s3,s]
e,p1x,p1y,q1x,q1y,r1,s1,r,s2,s3,s = [int(i,16) for i in tt]
P1 = E(p1x,p1y)
Q1 = E(q1x,q1y)

################################################################################# solve d1
PR.<k1,d1> = PolynomialRing(Zmod(n))
f1 = (s1*k1 - e)*d1 - r1
f2 = d1*k1*s2 + d1*s3 - r - s
res = f1.sylvester_matrix(f2, k1).det().univariate_polynomial().monic().roots()
d1 = int(res[1][0])

print(d1*P1 == G)

或者
from sage.all import *

a = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
b = 0x28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
p = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
n = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
x = 0x32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7
y = 0xBC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0
E = EllipticCurve(GF(p), [a, b])
G = E(x, y)

s = 0xcb524f49515c9a7387210ddcdbf1f32aad1c8806f01a362c62a5d6a5466da158

r = 0x8A6BB033033E79683E81FE36D6394262D451A3DB9D1A0C489D51543D22E67BC4
s2 = 0xB54A6668F644EC08D925552D45F66E348762B460693E7A68CBB0FDF38327DB45
s3 = 0xB50FAE013594F79192898FF7FC0A84D931B1EC56EF9174159023ACF1C708180D

e = 0xeaf0adee014bd35a12180bbc99292e3acf895203aa97f8dbbb760da04da844f6
r1 = 0x125fd6eb66351ca49073a6e55be1fa40cfd6662f80452a6bcea3b25bd69b6b26
s1 = 0x47baaef61c7a3c4c239fc2634ec25a2059d937026c6e0b72df1463fbba5b3a05

d2 = ZZ((s3 - s2) * inverse_mod(r, n) % n)

'''
s1*k1-e = d1^(-1) * r1
r1 = d1*(s1*k1-e)
r1 = d1*k1 * s1 - d1*e
s = d1*k1*s2 + d1*s3 -r
s*s1 = d1*k1*s1 * s2 + d1*s3*s1 - r*s1
s*s1 = (r1+d1*e)*s2 + d1 * s3*s1 - r*s1
'''
R = PolynomialRing(GF(n), 'x')
x = R.gens()[0]
f = (r1 + x*e)*s2 + x*s3*s1 - r*s1 - s*s1
ans = f.roots()

d1 = 90919127323695568397119051689582862352296983775157729258730148362152821090405
d2 = 75133153874808200698750375741973887146735262423059242244009334005845482114914
e = 0x9e810778a6b177c6aa1799365977adfbeef605c19b5ea917527d1541c1339019

k1 = 233
P = inverse_mod(d1, n) * G
Q = k1*G
r1 = ZZ(Q.xy()[0])
s1 = ZZ(inverse_mod(k1, n) * (e + inverse_mod(d1, n) * r1) % n)

k2 = 17
k3 = 71
R = k2*G + k3*Q
x1 = ZZ(R.xy()[0])
r = ZZ((e + x1) % n)
s2 = ZZ(d2 * k3 % n)
s3 = ZZ(d2 * (r+k2) % n)

s = (d1*k1*s2 + d1*s3 - r) % n
print(s)
print(hex(r)[2:])
print(hex(s)[2:])

来源： https://tangcuxiaojikuai.xyz/post/6452f9a0.html

posted @ 2024-10-07 12:09 渗透测试中心阅读(82) 评论(0) 编辑收藏举报

刷新页面返回顶部

渗透测试中心

2024熵密杯wp

第一部分：初始谜题

初始谜题一(300 pts)

初始谜题二(300 pts)

初始谜题三(300 pts)

第二部分：大型密码系统

flag1(600 pts)

flag2(900 pts)

flag3(500 pts)

flag4(1000 pts)

最终挑战 *

公告