Unity中的shadows（二）cast shadows

本文是Unity中的shadows系列的第二篇文章。上一篇文章主要介绍了不同光源下的阴影和阴影的一些设置参数。本篇着重研究阴影投射相关的内容。

投射阴影（平行光，聚光灯）

由于点光源的shadowmap是cube map，所以需要和平行光源，聚光灯分开处理。先看平行光源和聚光灯。在shadow caster阶段，unity提供了UnityClipSpaceShadowCasterPos和UnityApplyLinearShadowBias两个API。那么，现在ShadowCaster的代码变成了这样：

	float4 MyShadowVertexProgram (VertexData v) : SV_POSITION {
		float4 position =
			UnityClipSpaceShadowCasterPos(v.position.xyz, v.normal);
		return UnityApplyLinearShadowBias(position);
	}

	half4 MyShadowFragmentProgram () : SV_TARGET {
		return 0;
	}

UnityApplyLinearShadowBias

让我们看下这两个API的实现，首先是UnityApplyLinearShadowBias：

float4 UnityApplyLinearShadowBias(float4 clipPos)

{
    // For point lights that support depth cube map, the bias is applied in the fragment shader sampling the shadow map.
    // This is because the legacy behaviour for point light shadow map cannot be implemented by offseting the vertex position
    // in the vertex shader generating the shadow map.
#if !(defined(SHADOWS_CUBE) && defined(SHADOWS_CUBE_IN_DEPTH_TEX))
    #if defined(UNITY_REVERSED_Z)
        // We use max/min instead of clamp to ensure proper handling of the rare case
        // where both numerator and denominator are zero and the fraction becomes NaN.
        clipPos.z += max(-1, min(unity_LightShadowBias.x / clipPos.w, 0));
    #else
        clipPos.z += saturate(unity_LightShadowBias.x/clipPos.w);
    #endif
#endif

#if defined(UNITY_REVERSED_Z)
    float clamped = min(clipPos.z, clipPos.w*UNITY_NEAR_CLIP_VALUE);
#else
    float clamped = max(clipPos.z, clipPos.w*UNITY_NEAR_CLIP_VALUE);
#endif
    clipPos.z = lerp(clipPos.z, clamped, unity_LightShadowBias.y);
    return clipPos;
}

前面的宏是用来判断如果是点光源且当前的硬件平台支持depth cube map，就跳过bias的相关计算。bias的计算和是否UNITY_REVERSED_Z有关。如果定义了UNITY_REVERSED_Z，那么在clip space中近剪裁面的z值为1，远剪裁面的z值为0。使用reversed-z技术的原因是为了弥补深度缓存的精度问题。由于z不是均匀分布的，离近剪裁面越近的地方，z的精度越高，而越远的地方，z的精度越低。而如果用浮点数来保存z的值，浮点数又在值靠近0时有较高的精度，靠近1时精度较差。因此，为了让其互补，就将z的取值进行reverse，这样靠近1的z值虽然浮点精度有限，但是离近剪裁面会更近；同样地，靠近0的z值虽然离近剪裁面较远，但是浮点精度更高。

扯远了，继续看函数实现，我们可以看到一个神秘的unity_LightShadowBias，它是一个四维向量，保存与阴影相关的参数。这个值与光源类型有关，先看平行光源的情况。

当平行光源的bias值设置为0.05时，打开frame debugger定位到shadow caster阶段：

此时unity_LightShadowBias.x是一个比较小的负数，而不是简单的0.05。通过反复实验和猜测得出：

unity_LightShadowBias.x = -UNITY_MATRIX_P._33 * _Bias

代入截图中的值计算，-0.026 * 0.05 = -0.0013刚刚好。

再看聚光灯的情况，同样当聚光灯的bias值设置为0.05时，打开frame debugger定位到shadow caster阶段：

此时unity_LightShadowBias.x就是_Bias的值单纯取反得到。

最后看一下点光源：

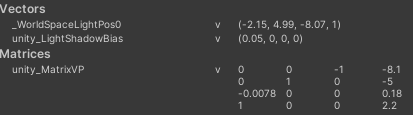
这个就十分nice了，直接就是_Bias的值。继续看代码，有个unity_LightShadowBias.x / clipPos.w的处理，这就有点奇怪了，一般除w的操作，都是在fragement shader中出现的，这里还是vertex shader阶段，除w作用是什么呢？由于光源空间的投影可能有两种，正交投影和透视投影，因此让我们分别来看下。

首先是正交投影，平行光源就是正交投影。我们可以打开frame debugger确认一下：

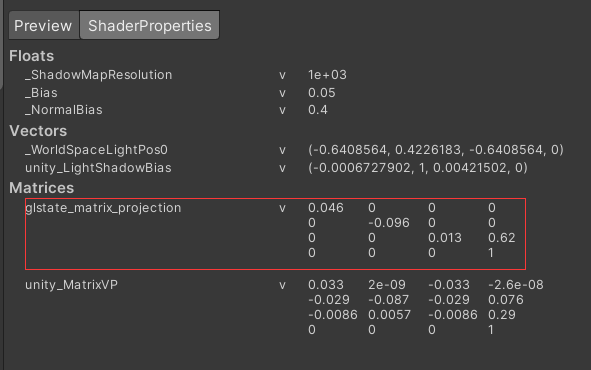
把矩阵写成数学形式为：

\[M = \begin{bmatrix} a & 0 & 0 & 0 \\ 0 & b & 0 & 0 \\ 0 & 0 & c & d \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

显然这是一个正交投影矩阵。对于相机空间中的任一点\(P(x,y,z,1)\)，变换到齐次剪裁空间后的\(P'\)坐标为：

\[P' = MP^T = \begin{bmatrix} a & 0 & 0 & 0 \\ 0 & b & 0 & 0 \\ 0 & 0 & c & d \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = (ax, by, cz + d, 1)^T \]

可以发现，对于正交投影，clipPos.w的值为1。所以除w这件事情对正交投影压根没有影响。那么，在先不考虑各种边界的情况下，就有：

        clipPos.z += -UNITY_MATRIX_P._33 * _Bias;

这里Unity需要乘上一个系数的原因就真相大白了。带有负号是因为RESERVE Z，这里不必考虑，_Bias这个值是暴露给使用者的参数，它的自身意义就是让物体在光源空间中往后偏移一个量，而无需考虑光源空间本身，换句话说就是物体在光源空间中延z方向往后偏移\(\Delta z\)，那么它在齐次剪裁空间中z的偏移量\(\Delta z'\)是多少？这个很好计算：

\[P_1 = (x,y,z,1) \\ P_2 = (x,y,z+\Delta z, 1) \\ P'_1 = (ax,by,cz+d,1) \\ P'_2 = (ax,by,c(z+\Delta z) +d, 1) = P'_1 + (0,0,c\Delta z, 0) \]

也就是说，在齐次空间中，要让z的值偏移\(c\Delta z\)才行。这个c恰恰就是上面提到的UNITY_MATRIX_P._33！Unity选择直接参数传递而不是在shader中计算的原因，猜测是传递不必要的矩阵到GPU上是一种浪费，而且对GPU而言这本身就是个常量，没必要在每个顶点上都去算一遍。

再来看透视投影，聚光灯就是透视投影。我们可以打开frame debugger确认一下：

把矩阵写成数学形式为：

\[M = \begin{bmatrix} a & 0 & 0 & 0 \\ 0 & b & 0 & 0 \\ 0 & 0 & c & d \\ 0 & 0 & -1 & 0 \end{bmatrix} \]

显然这是一个透视投影矩阵。对于相机空间中的任一点\(P(x,y,z,1)\)，变换到齐次剪裁空间后的\(P'\)坐标为：

\[P' = MP^T = \begin{bmatrix} a & 0 & 0 & 0 \\ 0 & b & 0 & 0 \\ 0 & 0 & c & d \\ 0 & 0 & -1 & 0 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = (ax, by, cz + d, -z)^T \]

同样，在先不考虑各种边界的情况下，就有：

clipPos.z += -_Bias / -viewPos.z;

这里对viewPos.z取负，是因为相机空间是右手坐标系，相机看向的是z轴负方向，所以viewPos.z < 0，而在剪裁空间又是左手坐标系，需要对z轴取反。

类似正交投影，我们假设物体在光源空间中延z方向往后偏移\(\Delta z\)，那么它在齐次剪裁空间中z的偏移量\(\Delta z'\)是多少？

\[P_1 = (x,y,z,1) \\ P_2 = (x,y,z+\Delta z, 1) \\ P'_1 = (ax,by,cz+d,-z) \\ P'_2 = (ax,by,c(z+\Delta z) +d, -(z + \Delta z)) \]

好像没那么直观，让我们继续往下推导：

\[P'_2 = (\dfrac{ax \cdot (-z)}{-(z + \Delta z)}, \dfrac{by \cdot (-z)}{-(z + \Delta z)}, \dfrac{(c(z+\Delta z) +d) \cdot (-z)}{-(z + \Delta z)}, -z) \]

这回x和y都变了。但其实也是正常的，毕竟对于透视投影来说，将一个物体往z方向平移，投影的位置还和位移前相同，那么它的x，y方向也需要平移。不过，这里我们不需要考虑x和y的部分。继续放大z的计算部分往下看：

\[\Delta z' = \dfrac{(c(z+\Delta z) +d) \cdot (-z)}{-(z + \Delta z)} - (cz +d) \\ = \dfrac{(c(z+\Delta z) +d) \cdot z - (cz+d)(z+\Delta z)}{(z + \Delta z)} \\ = \dfrac{-d\Delta z}{z + \Delta z} \]

对于同一个光源空间来说，d其实是一个常数，为了计算方便可以直接拿掉，而\(\Delta z\)和z本身相比，可以忽略不计，所以有：

\[\Delta z' = \dfrac{-d\Delta z}{z + \Delta z} \approx \dfrac{-\Delta z}{z} \]

这就和代码中的描述一致了。其实从直观上也好理解，这步操作是为了让物体在光源空间的不同位置往后偏移时，都能偏移相同的一个量，因为透视投影具有近大远小的性质，除z就是做了一个透视补偿。

再往下看代码，这里定义了一个clamped的分量，它在unity_LightShadowBias.y为1的时候生效。通过查阅资料可以知道，这个值只有在平行光源的情况为1，其他情况都为0。clamped所做的事情就是让clipPos.z不要超过近剪裁面，代表的是光源背面（近似）的点的z值。而平行光源是不存在光源背面这一概念的，理论上只要位于平行光源的光源空间内，就一定要跑一遍shadow caster。所以这么做的原因是为了防止裁掉平行光“背面”的点。

UnityClipSpaceShadowCasterPos

接下来看UnityClipSpaceShadowCasterPos：

float4 UnityClipSpaceShadowCasterPos(float4 vertex, float3 normal)
{
    float4 wPos = mul(unity_ObjectToWorld, vertex);

    if (unity_LightShadowBias.z != 0.0)
    {
        float3 wNormal = UnityObjectToWorldNormal(normal);
        float3 wLight = normalize(UnityWorldSpaceLightDir(wPos.xyz));

        // apply normal offset bias (inset position along the normal)
        // bias needs to be scaled by sine between normal and light direction
        // (http://the-witness.net/news/2013/09/shadow-mapping-summary-part-1/)
        //
        // unity_LightShadowBias.z contains user-specified normal offset amount
        // scaled by world space texel size.

        float shadowCos = dot(wNormal, wLight);
        float shadowSine = sqrt(1-shadowCos*shadowCos);
        float normalBias = unity_LightShadowBias.z * shadowSine;

        wPos.xyz -= wNormal * normalBias;
    }

    return mul(UNITY_MATRIX_VP, wPos);
}
// Legacy, not used anymore; kept around to not break existing user shaders
float4 UnityClipSpaceShadowCasterPos(float3 vertex, float3 normal)
{
    return UnityClipSpaceShadowCasterPos(float4(vertex, 1), normal);
}

unity_LightShadowBias.z存储了与normal dias相关的参数。这个值还与shadow map的贴图尺寸有关。而且通过实践可以发现，这个值只在平行光源的情况下有效，其他光源都是0。让我们回到之前的图：

我们要求的normal bias就是CG的长度，它等于DI：

\[CG = DI = DH \cdot sin\theta = \dfrac{1}{2}AB \cdot sin\theta \]

AB其实是光源视锥体大小与shadowmap尺寸的比值，可以理解成是shadowmap的一个texel所能覆盖的视锥体区域。这里也可以看出，shadowmap的精度越高，覆盖的光源视锥体区域越小，引起shadow acne的可能性也越小。

\[AB = \dfrac{frustumSize}{shadowMapSize} \]

从图中容易看出\(\theta\)其实就是光源与法线的夹角，所以：

\[sin\theta = \sqrt{1 - (N \cdot L)^2} \]

目前尚不清楚Unity是如何计算frustumSize的，但在某些情况下，这个frustumSize就是：

frustumSize = 2 / UNITY_MATRIX_P._11

也就得到：

\[CG = \dfrac{1}{MatrixP_{11} \cdot shadowMapSize} \cdot sin\theta \]

正弦前面这货就是unity_LightShadowBias.z（可能不准确）。

投射阴影（点光源）

现在让我们回到点光源来。对于点光源来说，ShadowCaster的代码是这样的：

	struct Interpolators {
		float4 position : SV_POSITION;
		float3 lightVec : TEXCOORD0;
	};

	Interpolators MyShadowVertexProgram (VertexData v) {
		Interpolators i;
		i.position = UnityObjectToClipPos(v.position);
		i.lightVec =
			mul(unity_ObjectToWorld, v.position).xyz - _LightPositionRange.xyz;
		return i;
	}

	float4 MyShadowFragmentProgram (Interpolators i) : SV_TARGET {
		float depth = length(i.lightVec) + unity_LightShadowBias.x;
		depth *= _LightPositionRange.w;
		return UnityEncodeCubeShadowDepth(depth);
	}

代码看上去很直观，除了最后的UnityEncodeCubeShadowDepth，看一下它是做什么的：

// Encoding/decoding [0..1) floats into 8 bit/channel RGBA. Note that 1.0 will not be encoded properly.
inline float4 EncodeFloatRGBA( float v )
{
    float4 kEncodeMul = float4(1.0, 255.0, 65025.0, 16581375.0);
    float kEncodeBit = 1.0/255.0;
    float4 enc = kEncodeMul * v;
    enc = frac (enc);
    enc -= enc.yzww * kEncodeBit;
    return enc;
}

float4 UnityEncodeCubeShadowDepth (float z)
{
    #ifdef UNITY_USE_RGBA_FOR_POINT_SHADOWS
    return EncodeFloatRGBA (min(z, 0.999));
    #else
    return z;
    #endif
}

因为有些硬件不支持渲染到浮点纹理，只能将一个浮点数拆成4个部分，分别存储到RGBA上。而不支持浮点纹理的硬件往往也不支持整数指令和位运算操作，就只能采用传统的加减乘除四则运算了。代码中kEncodeMul的值实际上是：

\[kEncodeMul = (255^0, 255^1, 255^2, 255^3) \]

我们希望把v表示成：

\[v = v_R + \dfrac{1}{255}v_G + \dfrac{1}{255^2}v_B + \dfrac{1}{255^3}v_A \\ \dfrac{1}{255} \leq v_R < 1 \\ \dfrac{1}{255} \leq v_G < 1 \\ \dfrac{1}{255} \leq v_B < 1 \\ \dfrac{1}{255} \leq v_A < 1 \\ \]

让我们对enc.x分量的计算过程进行分析，其他的分量也是类似的：

\[enc_x = v_R + \dfrac{1}{255}v_G + \dfrac{1}{255^2}v_B + \dfrac{1}{255^3}v_A \\ enc_y = v_G + \dfrac{1}{255}v_B + \dfrac{1}{255^2}v_A \\ enc_x = enc_x - enc_y \cdot \dfrac{1}{255} = v_R \]

对于点光源，我们显式地在fragment shader中返回了像素点的深度信息，这是因为点光源的cube map不一定支持depth，也就是硬件不一定会把深度信息自动写入cube map。Unity使用SHADOWS_CUBE_IN_DEPTH_TEX宏进行区分。