感慨
周五比赛的测试题,结果到比赛结束也没有读懂题意。。。给的样例太少了,我一直以为我是不是spfa敲错了。。。没想到中间还有卡的地方
分析
题目中的一句耐人寻味的话“路径上的所有点的出边所指向的点都直接或间接与终点连通。”就是这句话直接忽略掉了spfa才导致的WA。这句话的意思实际上是说如果这条路径上所有连通的点只要有一个点没有与终点连通,那么这条路就不合适。换句话说就是比如1-2-3-4是以1为起点4为终点的一条路,我们现在找到的一条。然后如果3-5-6意思是3和5和6又相连,其中如果5和6有一个点所连通的点里面没有到达终点的,那么3这个点就不合适了。我们假设只能由5-6,6没有除了5之外连通的点了,那么3这个点就是不合适的。就算这是你找到的最短路,那也是不合适的。还需要再找到比最短路长的合适的路
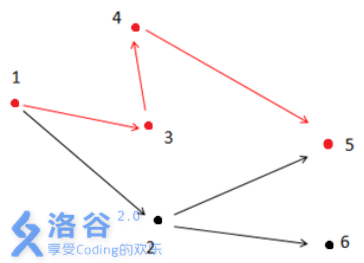
洛谷第二个样例的图(咱们比赛应该把样例2出上啊,要不看不懂题啊。。。也可能是我语文不好。。。)
其中红线是答案的路线
解法
①反向存边
第一遍我们要找到所有与终点连通的边,所以我们应该从终点开始bfs整个图,然后去寻找与终点连通的边,这里我们需要反向存边
②枚举各个顶点
这一步是为了确保上述分析中3这样的点的存在,把他们找出来。注意这个地方要开其他的临时的数组,避免寻找的时候出现混乱
③SPFA
直接把所有能符合规定的点入队spfa即可
④输出dis数组
这里注意判断条件,如果不连通直接-1
具体看下面的代码,代码里面也有注释
#include <bits/stdc++.h>
using namespace std;
//我这里用的是vector存边所以先开一个结构体
struct node
{
int to,cost;
};
//map是为了能够避免迷之re,然后long long是为了避免spfa int爆表成负数
map<long long,long long> vis,bk,bk1,dis,bk2;
//两个队列, q是spfa qq是bfs
queue<int> q,qq;
//两个存边的vector
vector <node> G1[10005];
vector <node> G2[10005];
const int inf=INT_MAX;
int main()
{
ios::sync_with_stdio(0);//关闭同步三步走,只要c++就要关同步
cin.tie(0);
cout.tie(0);
int n,m;
cin>>n>>m;//输入点和边的个数
while(m--)
{
int t1,t2;
cin>>t1>>t2;
G1[t2].push_back((node){t1,1});//反向存边
G2[t1].push_back((node){t2,1});//正向存边
}
int s,e;
cin>>s>>e;//输入s起点和e终点
for(int i=1;i<=n;i++)//初始化dis数组,为了spfa
dis[i]=i==s?0:inf;
qq.push(e);//从e开始bfs
bk2[e]=1;//bk2数组是给bfs剪枝用的
while(qq.size())
{
int f=qq.front();
qq.pop();
bk[f]=1;
vis[f]=1;
for(int i=0;i<G1[f].size();i++)//直接进行所有的遍历,如果满足条件那么就标记上
{
vis[G1[f][i].to]=1;//1号标记
bk[G1[f][i].to]=1;//2号标记
if(!bk2[G1[f][i].to])//剪枝,避免已经入队过的点重新入队
{
bk2[G1[f][i].to]=1;
qq.push(G1[f][i].to);
}
}
}
for(int i=1;i<=n;i++)//枚举各个点
{
if(!vis[i])//如果他与终点不连通
for(int j=0;j<G1[i].size();j++)
if(vis[G1[i][j].to])//如果他的连通的点与终点连通
bk[G1[i][j].to]=0;//去掉标记
}
q.push(s);//spfa起点入队
while(q.size())
{
int p=q.front();
q.pop();
bk1[p]=0;
if(bk[p])//如果是一个标记的点
{
for(int i=0;i<G2[p].size();i++)//老生常谈的spfa模板
{
if(dis[G2[p][i].to]>dis[p]+G2[p][i].cost)
{
dis[G2[p][i].to]=dis[p]+G2[p][i].cost;
if(!bk1[G2[p][i].to])
{
bk1[G2[p][i].to]=1;
q.push(G2[p][i].to);
}
}
}
}
}
if(dis[e]<INT_MAX)//判断一下条件输出dis数组即可
cout<<dis[e];
else
cout<<-1;
}


