什么是树状数组?
百度原文
·树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和,但是每次只能修改一个元素的值;经过简单修改可以在log(n)的复杂度下进行范围修改,但是这时只能查询其中一个元素####的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。
·这种数据结构(算法)并没有C++和Java的库支持,需要自己手动实现。在Competitive Programming的竞赛中被广泛的使用。树状数组和线段树很像,但能用树状数组解决的问题,基本上都能用线段树解决,而线段树能解决的树状数组不一定能解决。相比较而言,树
状数组效率要高很多。
经典图示
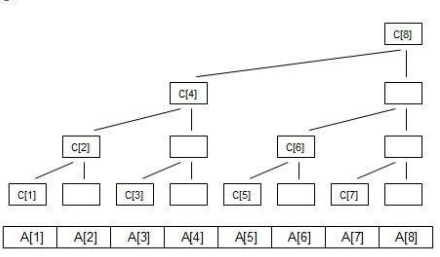
为什么要选择树状数组?
因为树状数组能够做到大数据下快速计算区间、区间异或和、区间乘积和区间最大值和最小值等基本上一切区间的操作。
怎么实现?
lowbit函数
什么是lowbit函数?
lowbit函数即为求二进制数的最右边的1的值,例如6(110)lowbit(6)=2;
怎么实现lowbit函数?
int lowbit(int x)
{
return x&(-x);
}
把这个数的二进制写出来,然后从右向左找到第一个1(这个1就是我们要求的结果,但是现在表示不出来,后来的操作就是让这个1能表示出来),这个1不要动和这个1右边的二进制不变,左边的二进制依次取反,这样就求出的一个数的补码,说这个方法主要是让我们理解一个负数的补码在二进制上的特征,然后我们把这个负数对应的正数与该负数与运算一下,由于这个1的左边的二进制与正数的原码对应的部分是相反的,所以相与一定都为0,;由于这个1和这个1右边的二进制都是不变的,因此,相与后还是原来的样子,故,这样搞出来的结果就是lowbit(x)的结果。
update函数
什么是update函数?
update函数即为更改单个值后树状数组的更新函数
怎么实现update?
void update(int x,int k)
{
for(int i=x;i<=n;i+=lowbit(i))
tree[i]+=k;
}
sum函数
什么是sum函数?
即为求前缀区间和的函数
怎么实现sum函数?
int sum(int x)
{
int ans=0;
for(int i=x;i;i-=lowbit(i))
ans+=tree[i];
return ans;
}
完整模板
#include <bits/stdc++.h>
using namespace std;
int tree[500010];
int n,m;
int lowbit(int x)
{
return x&(-x);
}
void update(int x,int k)
{
for(int i=x;i<=n;i+=lowbit(i))
tree[i]+=k;
}
int sum(int x)
{
int ans=0;
for(int i=x;i;i-=lowbit(i))
ans+=tree[i];
return ans;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
int a;
cin>>a;
update(i,a);
}
for(int i=1;i<=m;i++)
{
int t1,t2,t3;
cin>>t1>>t2>>t3;
if(t1==1)
update(t2,t3);
else
cout<<sum(t3)-sum(t2-1)<<endl;
}
}
改版树状数组
如何改版?
原来朴素的树状数组只是单个元素的更改以及求区间的答案,现在倒过来对区间元素的修改求单个元素的值
如何实现?
用普通的树状数组维护差分数组即可
基本思路
维护差分数组的值,更改区间和仅仅只需要更改区间的左端点和右端点+1的值,然后输出一个原数组的项,那么就是求差分数组的前i项和
完整模板
#include <bits/stdc++.h>
using namespace std;
int tree[500010];
int n,m;
int lowbit(int x)
{
return x&(-x);
}
void update(int x,int k)
{
for(int i=x;i<=n;i+=lowbit(i))
tree[i]+=k;
}
int sum(int x)
{
int ans=0;
for(int i=x;i;i-=lowbit(i))
ans+=tree[i];
return ans;
}
int main()
{
cin>>n>>m;
int last=0;
for(int i=1;i<=n;i++)
{
int a;
cin>>a;
update(i,a-last);
last=a;
}
for(int i=1;i<=m;i++)
{
int t1;
cin>>t1;
if(t1==1)
{
int t2,t3,t4;
cin>>t2>>t3>>t4;
update(t2,t4);
update(t3+1,-t4);
}
else
{
int t2;
cin>>t2;
cout<<sum(t2)<<endl;
}
}
}


