对泰勒公式又有了新的认识

之前的泰勒公式只用在了做极限上面，日日的做极限直接背过了好几个常用的展开，直到今天才发现原来我之前连泰勒公式定义都没搞明白。

当然浅显易懂的泰勒就是让你求个极限展开然后多加一个\(O(x^n)\)之类的东西。

不过正统的泰勒是一个函数逼近的玩意，这个类似于之前搞过的Simpson积分法，也是用多项式去拟合。

看这个定义肯定觉得很熟悉，不过实际上他还有一层关系在于我可以选取任意的\(x_0\)去做，然后只要我当前要算的\(x\)在\(x_0\)邻域内能求到那些导数，那就是可以的了。

所以实际上来说\(x_0\)还是很自由的了，之前并没有这种理解，而且要拟合的\(f(x)\)也是很自由的，可以用任意的\(x_0\)拟合。

然后就是今天的一个小疑问，

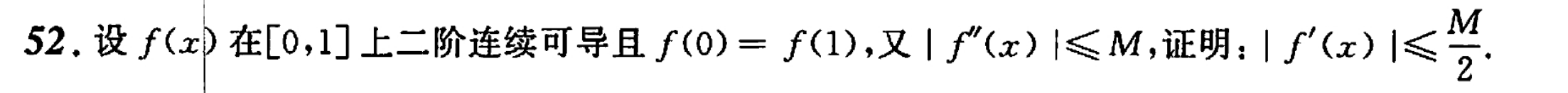
这玩意我搞了一阵子，没搞出来，答案是说要用泰勒，但是他泰勒我又看了一阵子

发现不应该都是\(x\)吗怎么还不一样，这就是泰勒还有的两个小贱的地方了，也就是两个余项。所谓余项就是拟合的过程中肯定要出现误差，我再给他加上。

两个余项对于考研来说，就是为了做题服务的，一个叫做拉格朗日余项，也就是我能展开到\((n+1)\)阶导数，但是我就展开到\(n\)阶，第\((n+1)\)阶导数我就给他上面的\(x_0\)换一个字母，然后这个字母介于\(x_0\)和\(x\)之间。。。。实际上没啥用，就是换个字母，做题的时候注意一下严谨性就好，就是玩。

另一个就是常见的佩亚诺余项，多一个高阶无穷小，实际上也就是玩。

不过对于做极限用泰勒的更深层的含义，实际上就是我选取\(x_0=0\)这个就转换成了一个叫做麦克劳林公式的玩意，实际上还是泰勒，然后我把要求的极限式子当作\(f(x)\)然后用这个\(x_0=0\)去拟合，算出来的\(f(x)\)是一个多项式再加一个佩亚诺余项，然后用这个多项式去\(x->0\)就好算了。