一文带你零基础深入理解随机变量，概率分布与统计量

一. 随机事件与概率

1.1 随机现象

在自然界和人类活动中，发生的现象多种多样，比如下列这些现象：

1. 偶数能被2整除　　　　　　　　　　　　2. 光的速度是常数　　　　　　　  3. 一家门店一天之内的订单量

4. 一个新生儿可能是男生也可能是女生　　  5. AB实验存在对照组和实验组　　 6. 李华上厕所的时间

不难发现，其中①②⑤这类现象在一定条件下必然发生，我们称这类现象是确定性现象。在③④⑥现象中，事先无法预知会出现哪个结果，我们称这类结果不确定的现象为随机现象。

 

由于随机现象结果在一次实验中不缺定的，在大量重复试验中结果将呈现某种规律性，例如相对比较稳定的性别比例，这种规律性称为统计规律性。为了研究随机现象的统计规律性，就要对客观事物进行观察，观察的过程叫随机试验（简称试验）。例如，为了研究一家门店的客流情况，可以反复地观察并记录门店的客流。

 

随机试验有三个特点：（1）在相同的条件下试验可以重复进行；（2）每次试验的结果不止一种，但是试验之前必须明确试验的所有可能结果；（3）每次试验将会出现什么样的结果是事先无法预知的．

 

PS：实验：为了检验某种科学理论或假设而进行某种操作或从事某种活动。试验：为了察看某事的结果或某物的性能而从事某种活动。

 

1.2 样本空间

随机试验的一切可能结果组成的集合称为样本空间，记为Ω={ω}，其中ω表示试验的每一个可能结果，又称为样本点，即样本空间为全体样本点的集合。

下面给出以③④⑥为随机试验的样本空间：Ω3={0, 1, 2, ..., n, ...}，Ω4={'Male'，'female'}，Ω6={t: t>0}，样本空间中的元素可以是数，也可以不是数．从样本空间中含有样本点的个数来看，可以是有限个也可以是无限个；可以是可列个也可以是不可列个。

 

1.3 随机事件

在随机试验中，常常会关心其中某一些结果是否出现．例如，一家门店的客流，关心客流是否低于800；李华上厕所的时间是否超过20分钟等．这些在一次试验中可能出现，也可能不出现的一类结果称为随机事件，简称为事件，随机事件通常用大写字母A，B，C，…表示。例如关心客流是否低于800，定义A=“门店客流大于800”是一个可能发生也可能不发生的随机事件，可描述为A={n: n>800 | n ∈N}，它是样本空间Ω={n: n ∈N}的一个子集．所以，从集合的角度来说，样本空间的部分样本点组成的集合称为随机事件。

必然事件：Ω　　不可能事件：∅　

 

1.4 概率的定义和性质

在n次试验中如果事件A出现了a次，则称比值a/n为这n次试验中事件A出现的频率．a称为事件A发生的频数．概率的统计定义为：随着试验次数n的增大，频率值逐步“稳定”到一个实数，这个实数称为事件A发生的概率。(还有公理化定义)

概率的性质

① P(Ω) = 1　　② P(∅) = 0　　③  

 

1.5 条件概率，全概率和贝叶斯公式

条件概率是指在某随机事件A发生的条件下，另一随机事件B发生的概率，记为P（B|A），它与P（B）是不同的两类概率．设E是随机试验，Ω是样本空间，A，B是随机试验E上的两个随机事件且P（A）>0，称 P(B | A) = P(AB) / P(A) 为在事件A发生的条件下事件B发生的概率，称为条件概率，记为P(B|A)。例如：假设一批顾客中有客单为25元，35元，50元的顾客共200人，100人， 50人，现从中抽取一位顾客，发现其客单不是50元，则抽取的顾客客单为25元的概率可表示为 P(客单为25 | 客单不为50)

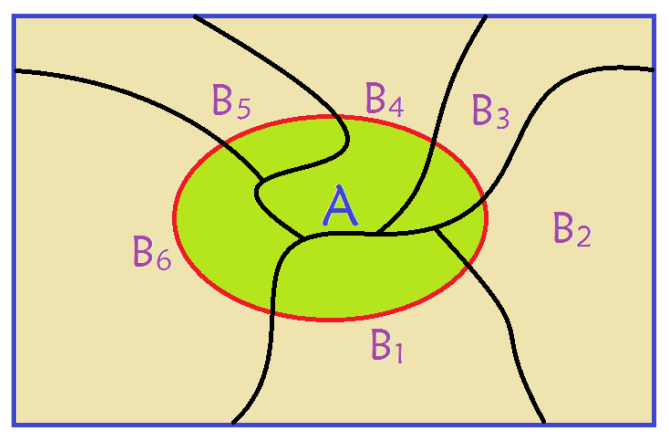
设B1，B2，…，Bn为样本空间Ω的一个完备事件组，且P（Bi）>0（i=1，2，…，n），A为任一事件，则

其中，完备事件组即对样本空间的一个分割。

设B1，B2，…，Bn为样本空间Ω的一个完备事件组，且P(Bi) > 0 (i=1，2，…，n)，A为满足条件P(A)＞0的任一事件，则

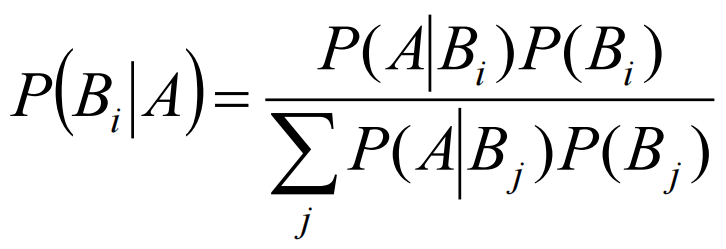
以下图为例：其中B1，B2, ..., B6，对整个样本空间进行了划分，他们之间两两的交集为空集，并且并集为整个样本空间。

思考题：n（n≤365）个人中至少有两个人的生日相同的概率是多少？

 

二. 随机变量与分布

2.1 随机变量的定义

在随机试验E中，Ω是相应的样本空间，如果对Ω中的每一个样本点ω，有唯一一个实数X（ω）与它对应，那么就把这个定义域为Ω的单值实值函数X=X（ω）称为（一维）随机变量．随机变量一般用大写字母X，Y等来表示，随机变量的取值一般用小写字母x，y等来表示．如果一个随机变量仅可能取有限或可列个值，则称其为离散型随机变量．如果一个随机变量的取值充满了数轴上的一个区间（或某几个区间的并），则称其为非离散型随机变量．连续型随机变量就是非离散型随机变量中最常见的一类随机变量．

随机变量的定义可直观解释为：随机变量X是样本点的函数，这个函数的自变量是样本点，可以是数，也可以不是数，定义域是样本空间，而因变量必须是实数．这个函数可以让不同的样本点对应不同的实数，也可以让多个样本点对应于一个实数．

 

2.2 随机变量的分布函数

设X是一个随机变量，对于任意实数x，称函数 F(x) = P(X≤x)，-∞<x<+∞为随机变量X的分布函数．对任意的两个实数-∞＜a＜b＜+∞，有 P(a<X≤b) = F(b) - F(a)．因此，只要已知X的分布函数，就可以知道 X 落在任一区间（a，b］内的概率，所以说，分布函数可以完整地描述一个随机变量的统计规律性．

从这个定义可以看出: (1) 分布函数是定义在（-∞，+∞）上，取值在［0，1］上的一个函数；(2) 任一随机变量X都有且仅有一个分布函数，有了分布函数，就可计算与随机变量X相关事件的概率问题．

例1. 设一盒子中装有10个球，其中5个球上标有数字1，3个球上标有数字2，2个球上标有数字3．从中任取一球，记随机变量X表示为“取得的球上标有的数字”，求X的分布函数F(x).

　　解: 根据题意可知，随机变量X可取1，2，3，可知对应的概率值分别为0.5，0.3，0.2．分布函数的定义为 F(x) = P(X≤x)，因此当 x<1 时，概率 P(X≤x) = 0；当1≤x<2时，概率P（X≤x）=P（X=1）=0.5；当2≤x<3时，概率P（X≤x）=P（X=1）+P（X=2）=0.5+0.3=0.8；当x≥3时，随机事件{X≤x}为必然事件，因此P（X≤x）=1，即 P(X≤x) = P(X=1) + P(X=2) + P(X=3) = 0.5 + 0.3 + 0.2 = 1．

 

 

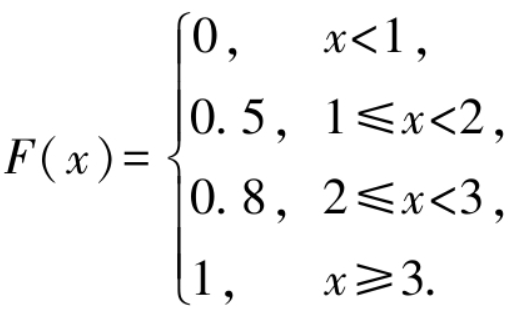
2.3 离散型随机变量及其分布律

设E是随机试验，Ω是相应的样本空间，X是Ω上的随机变量，若X的值域（记为ΩX）为有限集或可列集，此时称X为（一维）离散型随机变量．若一维离散型随机变量X的取值为x1，x2，…，xn，…，称相应的概率P(X=xi) = pi，i=1，2，…为离散型随机变量X的分布律(或分布列、概率函数)．若一维离散型随机变量X的取值为x1，x2，…，xn，…，称相应的概率P(X=xi)=pi，i=1，2，…为离散型随机变量X的分布律(或分布列、概率函数)．

 

2.3 连续型随机变量及其密度函数

连续型随机变量的取值充满了数轴上的一个区间（或某几个区间的并），在这个区间里有无穷不可列个实数，因此当我们描述连续型随机变量时，用来描述离散型随机变量的分布律就没法再使用了，而要改用概率密度函数来表示．设E是随机试验，Ω是相应的样本空间，X是Ω上的随机变量，F(x) 是X的分布函数，若存在非负函数 f(x) 使得

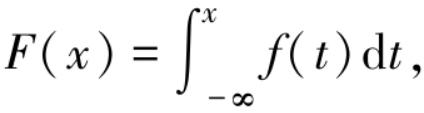
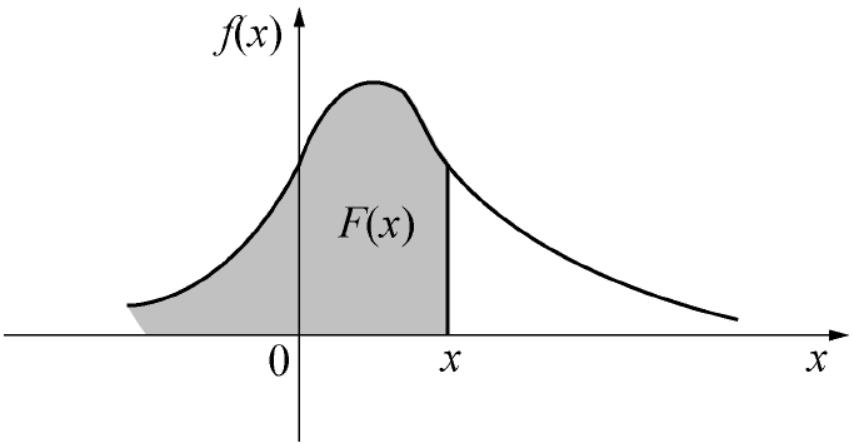
则称X为 (一维) 连续型随机变量，f(x) 称为X的 (概率) 密度函数，满足：(1) 非负性 f(x) ≥ 0，-∞<x<+∞；(2) 规范性

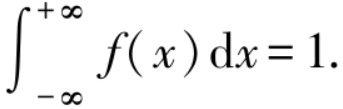
概率密度函数 f(x) 与分布函数 F(x) 之间的关系如图所示，F(x) = P(X≤x) 恰好是 f(x) 在区间 (-∞，x] 上的积分，也即是图中阴影部分的面积．

连续型随机变量具有下列性质: (1)分布函数 F(x) 是连续函数，在 f(x) 的连续点处，F′(x) = f(x) ；（2）对任意一个常数c，-∞<c<+∞，P(X=c) = 0，所以，在事件 {a≤X≤b} 中剔除 X=a 或剔除 X=b ，都不影响概率的大小，即P(a≤X≤b) = P(a<X≤b) = P(a≤X<b) = P(a<X<b)．需注意的是，这个性质对离散型随机变量是不成立的，恰恰相反，离散型随机变量计算的就是“点点概率”．

 

2.3 常见的离散型和连续型随机变量

常见的离散型随机变量：二项分布，泊松分布，超几何分布，几何分布与负二项分布......

常见的连续型随机变量：均匀分布，指数分布，正态分布，几何分布与负二项分布......

 

三. 随机变量的数字特征

3.1 期望与方差

离散型随机变量X的数学期望，也称作期望或均值，计算公式如下：

连续型随机变量X的数学期望，也称作期望或均值，计算公式如下：

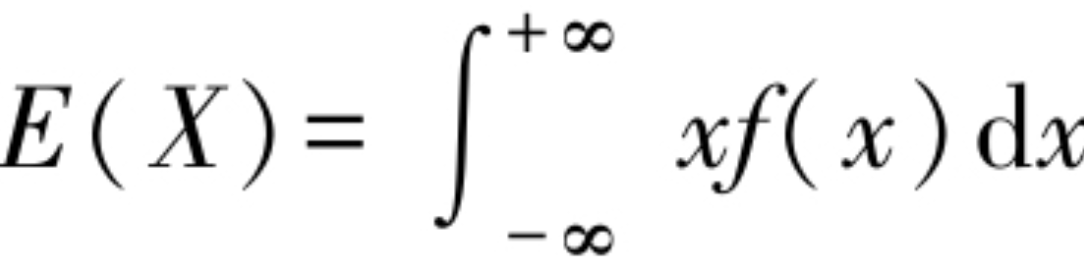
设X是一个随机变量，如果E{[X-E(X)]2}存在，则称

为随机变量X的方差．称方差 D(X) 的算术平方根

为随机变量X的标准差．

在机器学习的建模中，通常会出数据进行标准化，标准化的计算公式为：

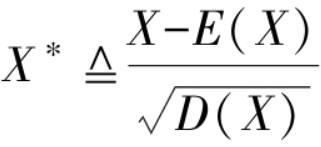
X*为X的标准化随机变量，标准化随机变量将其中心平移至原点，使其分布不偏左也不偏右，其期望为0；同时将随机变量取值压缩至原来的 1/sqrt(D(x)) 使其分布不疏也不密，压缩改变了分布的波动程度，方差变为1，这就是“标准化”的含义.

 

3.2 协方差

协方差：设（X，Y）是二维随机变量，如果E{ [ X - E(X) ] [ Y - E(Y) ] }存在，则称：

协方差反映了X和Y之间的关系，究竟是什么关系？可设Z = [X-E(X)][Y-E(Y)]，cov(X, Y) = E(Z)．若cov(X, Y) > 0，事件{ Z > 0 }更有可能发生，即事件{ X > E(X) } ∩ { Y > E(Y) }或{ X < E(X) } ∩ { Y < E(Y) }发生的可能性更大，说明X和Y均有同时大于或同时小于各自平均值的趋势；若cov(X, Y) < 0，事件{ Z < 0 }更有可能发生，即事件{ X > E(X) } ∩ { Y < E(Y) }或{ X < E(X) } ∩ { Y > E(Y) }发生的可能性更大，说明X和Y中有一个有大于其平均值的趋势另一个有小于其平均值的趋势．所以说协方差反映了随机变量X和Y之间“协同”变化的关系．当Y就是X时，cov(X, Y) = cov(X, X) = D(X) 协方差即为方差，这就是我们称其为协方差的原因．

 

3.3 相关系数

协方差考察了随机变量之间协同变化的关系，但在使用中存在这样一个问题．例如，要讨论新生婴儿的身高X和体重Y的协方差，若采用两种不同的单位，米和千克或者厘米和克，后者协方差是前者的100000倍！由于量纲的不同导致X与Y的协方差前后不同．为避免这样的情形发生，将随机变量标准化，再求协方差cov(X*，Y*)，这就是随机变量X和Y的相关系数，又称为标准化协方差．所以有相关系数的定义如下: 

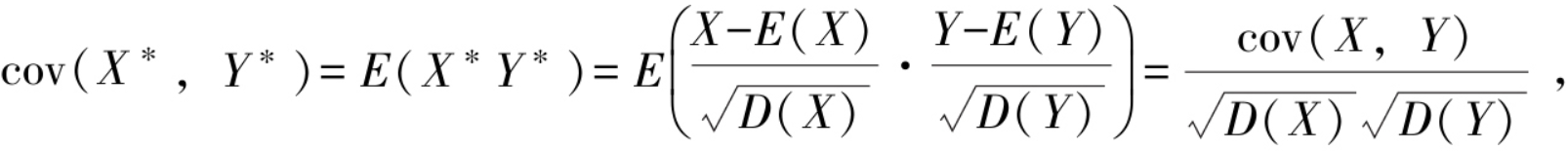
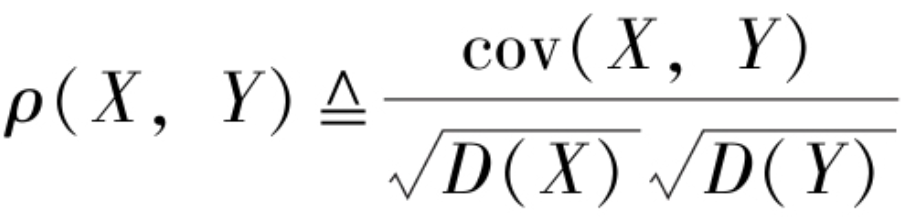
当|ρXY|=1时，（X，Y）的取值（x，y）在直线y=ax+b上的概率为1，称X与Y完全线性相关；

当ρXY=1时，（X，Y）的取值（x，y）在斜率大于0的直线y=ax+b上的概率为1，称X与Y完全正线性相关；

当ρXY=-1时，（X，Y）的取值（x，y）在斜率小于0的直线y=ax+b上的概率为1，称X与Y完全负线性相关．

当ρXY>0时，称X与Y正线性相关；当ρXY<0时，称X与Y负线性相关．

随机变量相互独立和线性无关都刻画了随机变量之间的关系，相互独立时一定线性无关，但反之不一定成立，例如下面的例子．

 

3.4 其他数字特征

对于随机变量X，X的k阶原点矩为：

 X的k阶中心矩为：

 

其中，期望为一阶原点矩，方差/标准差为二阶中心矩，变异系数为标准差和均值的绝对值的比值，偏度与三阶中心距相关，用于衡量随机变量分布的不对称性，峰度为与四阶中心矩相关，用于衡量概率密度在均值处峰值的高低特征。

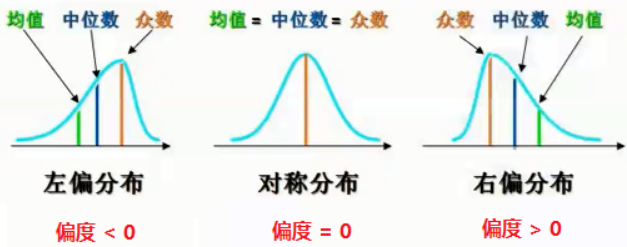
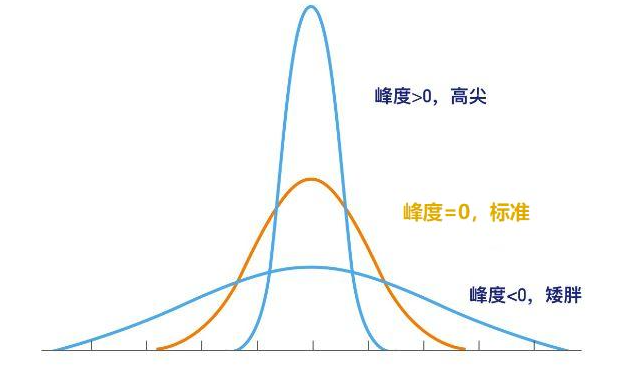
关于矩：https://www.bilibili.com/read/cv25074265/ 

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 

如何在生活中运用概率论？

费马—帕斯卡系统与世界的运转方式惊人地一致，是基本的公理，你真的必须得拥有这种技巧。——查理·芒格

 

在知识、能力、努力、耐心这些所有的品质中，查理芒格最看重的是理性。查理芒格说：“你必须看到这个世界真实的样子，而不是你以为的样子、或者你希望的样子，只有这样你才能做出正确的选择。”费马帕斯卡系统就是认识真实世界的基本工具。

 

费马帕斯卡系统是现代概率论的基础，来自一个概率论中的经典问题——点数问题（Problem of points），也叫赌注分配。

 

达芬奇的数学老师，帕西奥利最早在他的教科书中提到这个问题：说是A和B两个人，筹码相同，玩一种公平的、概率为1/2（类似掷硬币）的游戏。两人约定某个人赢到第10次的时候，游戏结束，赌注全部归胜者。但是游戏如果没有结束，筹码怎么分才合理呢？比如A赢了7次、B赢了6次。应该怎么分？

 

早期的两种观点：

1、按赢的次数来分，比如7：6，A拿到7/13，B拿到6/13。

这种分法问题很大，如果A赢了一次，游戏就结束。那么赢的次数是1：0，A赢了一次就拿走全部赌注，那肯定不合适。

 

2、赌注的分配应该考虑到两人比分的差距和游戏的总盘数。

这个分法有进步，但是也有问题，比如4：1和9：6，比分差距一样，但是区别很大，因为前者变数还比较大，而后者结局已经很明朗了。

直观的感觉是，赢的次数多的理应分得更多，但是具体应该分多少呢？

 

后来，费马和帕斯卡通过书信的形式讨论解决了这个问题。事实上，已经完成的赌局盘数不重要，决定胜负概率的是后面应该继续进行的盘数上。总数10盘的（7：5）的局和总数20盘的（17：15），领先者的机会是一样的。所以应该关注的是，剩下需要去完成的盘数。

 

我们可以把问题简化为：A和B两个人，筹码相同，玩掷硬币游戏。先赢3次赢得全部赌注，假设现在A赢了2次，B赢了1次，赌注该怎么分？

 

费马的方法：结束赌局，最多还要2局，结果有四种可能，且概率相等。

A胜A胜

A胜B胜

B胜A胜

B胜B胜

所以，A、B获胜概率分别为3/4，1/4，分配方式应该是3：1。

 

帕斯卡的方法：

第一局A胜：A得到全部赌注。

第一局A输：两人平分赌注。

两种概率相同。

所以，A、B获胜概率分别为3/4，1/4，分配方式应该是3：1。

 

如果你们懂得基本的心理学原理，就能理解人们做不到这一点的原因。其实很简单：大脑的神经系统是经过长期的基因和文化进化而来的，它并不是费马—帕斯卡系统，它使用的是非常粗略而便捷的估算，里面有一点费马—帕斯卡系统的元素，但是不精准。—— 查理.芒格

 

至此以后，“不可知”变成了“不确定”，“不可知”意味着对未来毫无办法，“不确定”意味着我们可以知道概率从而进行预测，这两者的差异可以说是天差地别。感觉概率在50%左右，和知道概率是50.1%，这两者的差异同样是天差地别。

 

决策树思维模型：http://www.360doc.com/content/22/0805/02/80114637_1042621529.shtml