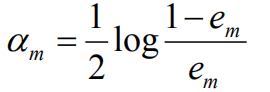Adaboost原理及相关推导
提升思想
一个概念如果存在一个多项式的学习算法能够学习它,并且正确率很高,那么,这个概率是强可学习的。一个概念如果存在一个多项式的学习算法能够学习它,并且学习的正确率仅比随机猜测略好,那么,这个概念是弱可学习的。强可学习与弱可学习是等价的。在学习中,如果已经发现了弱学习算法,那么是否能够将其提升为强学习算法呢?、
Adaboost
设训练数据集T={(x1,y1),(x2,y2),(xN,yN)},对数据集进行初始化训练数据的权重分布:
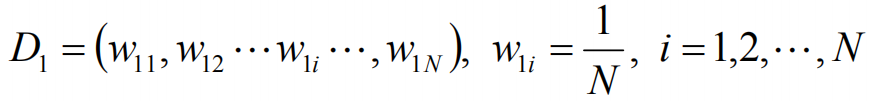
对于m=1,2,3······M,步骤如下:
使用具有权值分布Dm的训练数据集学习,得到基本分类器:
![]()
计算Gm(x)在训练数据集上的分类误差率:
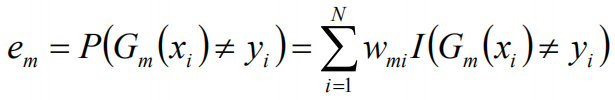
计算Gm(x)的系数:
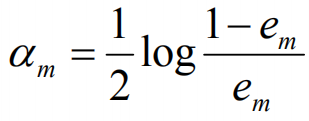
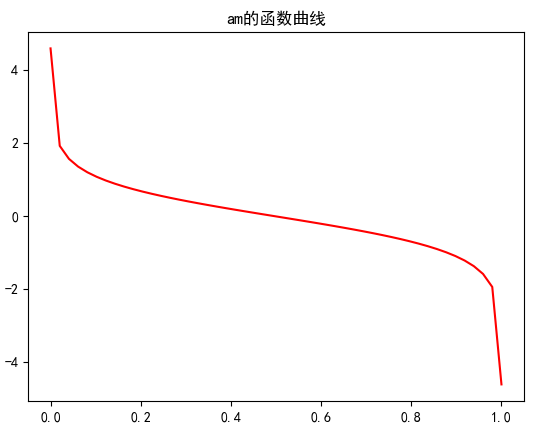
更新训练数据集的权值分布:
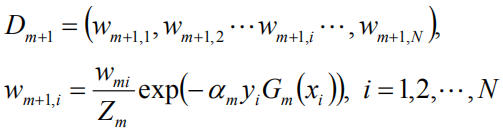
这里,Zm是规范化因子:
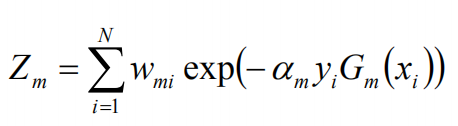
这里的规范化因子仅仅是要归一化。
基本分类器的线性组合
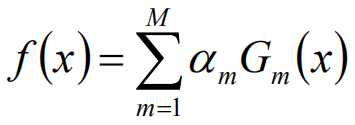
最终得到的分类器为:
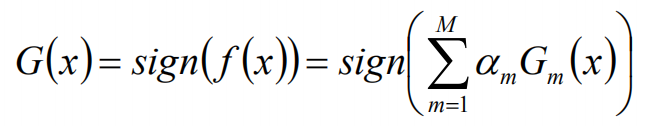
Adaboost中的误差上限
根据误差计算公式,有如下等式:
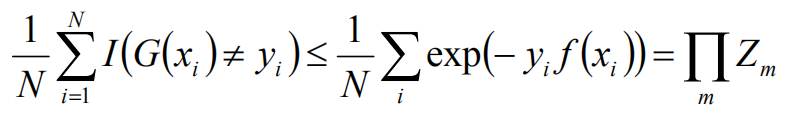
当G(xi)不等于yi时,yi*f(xi)<0,故exp(-yi*f(xi))>=1,前半部分得证,对于后面的等号,如下:
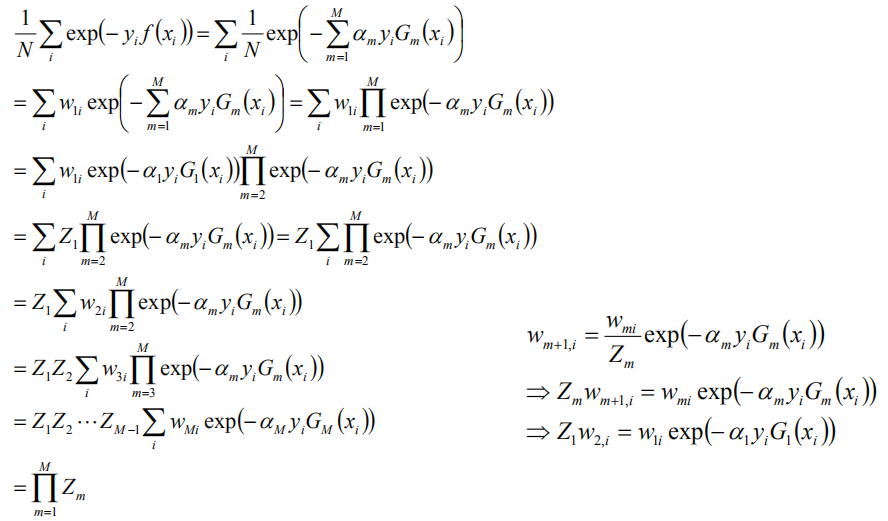
由此,可以计算得到训练的误差界,如下:
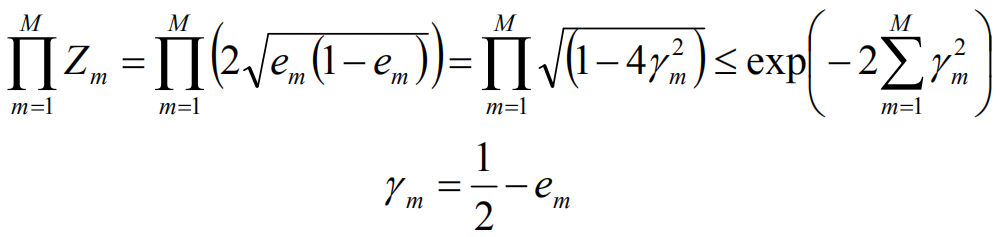
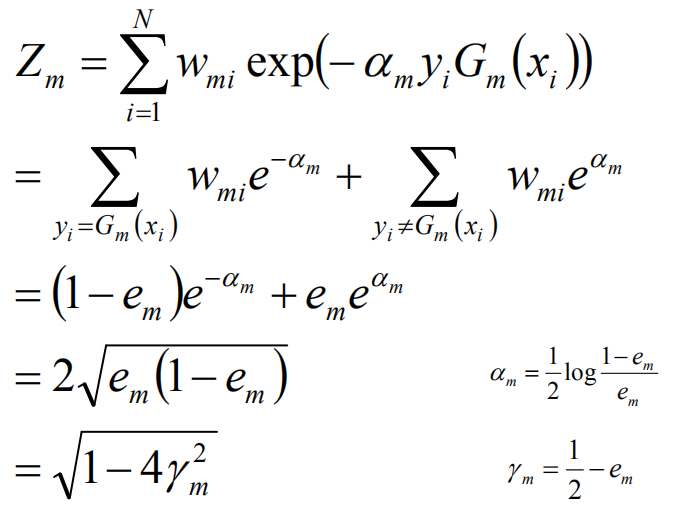
取r1,r2的最小值,记做r
Adaboost算法解释
Adaboost算法是模型为加法模型,损失函数为指示函数,学习算法为前向分布算法时的二分类学习算法
前向分步算法
对于下面加法模型:
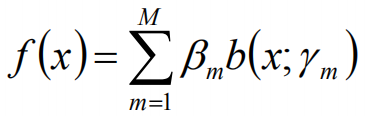
其中,b()函数为基函数,bm为基函数系数,rm为基函数的参数
前向分步算法在给定训练数据及损失函数L(y,f(x))的条件下,学习加法模型f(x)成为经验风险极小化,即损失函数极小化问题:
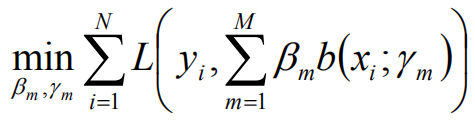
算法简化:如果能够从前向后,每一步只学习一个基函数及其系数,逐步逼近上式,即每一步只优化:
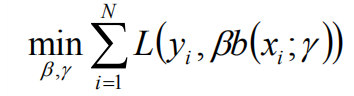
前向分布算法框架
输入:
训练数据集T,损失函数L(y,f(x)),基函数集{b(x;r)}\
输出:
加法模型f(x)
算法步骤:
初始化f0(x)=0
对于m=1,2,·······M
极小化损失损失函数:
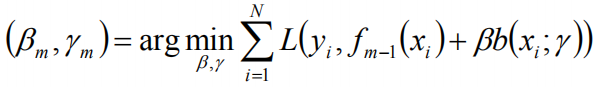
得到参数,b和r,在更新当前模型:
![]()
Adaboost算法是前向分布算法的特例,模型是由基本分类器组成的加法模型,损失函数是指数函数:
![]()
推导与证明
假设经过m-1轮迭代,前向分布算法已经得到fm-1(x):

在第m轮迭代得到am,Gm(x),fm(x),目标是使前向分布算法得到的am和Gm(x)使fm(x)在训练数据集T上的指数损失最小:
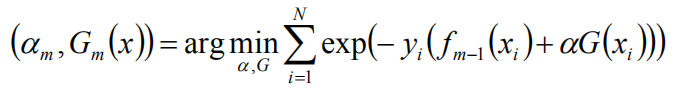
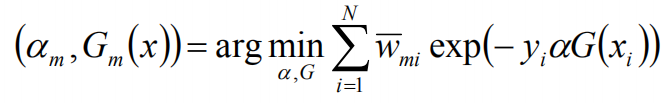
![]()
wmi既不依赖α也不依赖G,所以与最小化无关。但依赖于fm-1(x),所以,每轮迭代会发生变化。
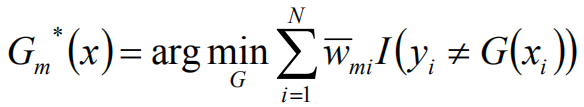
计算权值:
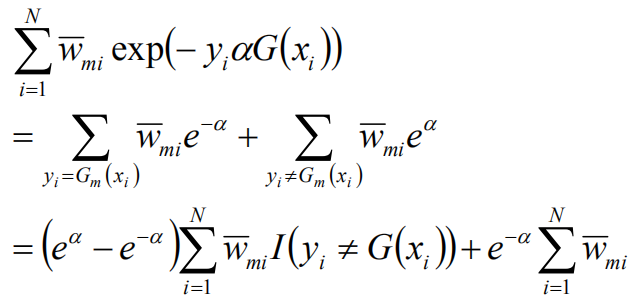
将G(x)带入
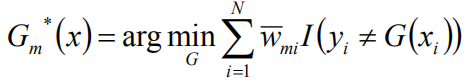
求导计算,得到:

分类错误率:
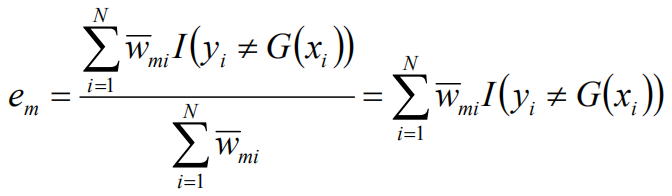
权值更新:
![]()
![]()
![]()
权值和错误率的关键解释:
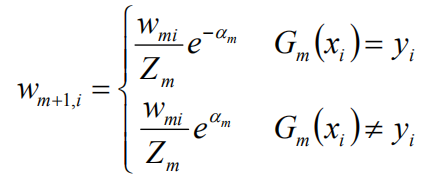
二者做除,得到:
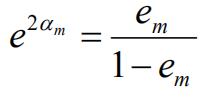
从而: