常见基本数据结构——树，二叉树，二叉查找树，AVL树

常见数据结构——树

处理大量的数据时，链表的线性时间太慢了，不宜使用。在树的数据结构中，其大部分的运行时间平均为O(logN)。并且通过对树结构的修改，我们能够保证它的最坏情形下上述的时间界。

树的定义有很多种方式。定义树的自然的方式是递归的方式。一棵树是一些节点的集合，这个集合可以是空集，若非空集，则一棵树是由根节点r以及0个或多个非空子树T1,T2,T3,......,Tk组成，这些子树中每一棵的根都有来自根r的一条有向的边所连接。

从递归的定义中，我们发现一棵树是N个节点和N-1条边组成的，每一个节点都有一条边连接父节点，但是根节点除外。

具有相同父亲的节点为兄弟，类似的方法可以定义祖父和孙子的关系。

从节点n1到nk的路径定义为节点n1，n2，...，nk的一个序列，并且ni是ni+1的父亲。这个路径的长是路径上的边数，即k-1。每个节点到自己有一条长为0的路径。一棵树从根到叶子节点恰好存在一条路径。

对于任意的节点ni，ni的深度为从根到ni的唯一路径长。ni的高是从ni到一片叶子的最长路径的长。因此，所有的树叶的高度都是0，一棵树的高等于它的根节点的高。一棵树的深度总是等于它最深叶子的深度；该深度等于这棵树的高度。

 

树的实现

实现树的一种方法可以是在每一个节点除数据外还要有一些指针，使得该节点的每一个儿子都有一个指针指向它。但是由于每个节点的儿子树可以变化很大而且事先不知道，故在各个节点建立子节点的链接是不可行的，这样将会浪费大量的空间。

实际的做法很简单：将每个节点的所有儿子都放在树节点的链表中。下面是典型的声明：

typedef struct TreeNode *PtrToNode
struct TreeNode{
　　ElementType Element;
　　PtrToNode FirstChild;
　　PtrToNode NextSibling
}

下面是儿子兄弟表示法的图示：

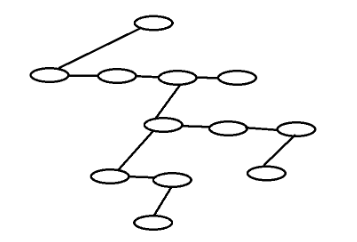
树的遍历及应用

一个常见的使用是操作系统中的目录结构。unix中的目录就是含有它的所有儿子的一个文件，下面是一个打印目录的例子，输出的格式是：深度为di的文件的名字将被di次跳格tab后缩进：

static void
ListDir(DictoryOrFile D, int Depth){
　　if(D is a legitimate entry){
　　　　PrintName(D, Depth);
　　if(D is a directory)
　　　　for each childm C, of D
　　　　　　ListDir(C, Depth + 1);
　　}
}

void
ListDirectory(DirectoryOrFile D){
　　ListDie(D, 0);
}

上述的遍历策略叫做先序遍历。在先序遍历中，对节点的处理工作是在他的诸子节点被处理之前进行的。另一种遍历树的方法是后序遍历。在后序遍历中，每一个节点处理的工作是在他的诸子儿子节点计算之后进行的。

 

记录一个目录大小的例程

static void SizeDirectory(Directory D){
　　int TotalSize=0;
　　if(D is a legitimate entry){
　　　　for each child, C of D:
　　　　　　TotalSize +=SizeDirectory(C);
　　}
　　return TotalSize;
}

 

二叉树

二叉树是一种树，他的每个节点都不能有多于两个的儿子。二叉树的一个性质是平均二叉树的深度要比N小的多，分析表明平均的深度为O(sqrt(N))，而对于特殊的二叉树而言，其深度的平均值是O(logN)的。

对于二叉树的实现，最多有两个儿子，我们可以用指针直接指向它们。在声明中，一个节点就是由Key(关键字)信息加上两个指向其他节点的指针组成的结构。

typedef struct TreeNode *PtrToNode;
typedef struct PtrToNode Tree;
struct TreeNode{
　　ElementType Element;
　　Tree Left;
　　Tree Right;
};

二叉树上就是图，在画二叉树的时候，我们一般不会画出NULL指针，因为具有N个节点的每一棵二叉树都将需要N+1个NULL指针。二叉树有许多与搜索无关的重要应用。二叉树的重要用处之一是在编译器的设计原则领域。

 

表达式树

下面是一个表达式树的例子：

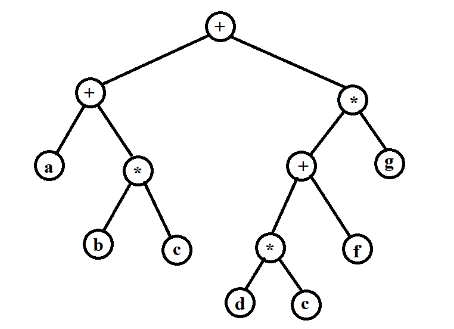
表达式树的树叶是操作数，比如常数或者变量，而其他的节点为操作符。由于这里所有操作都是二元的，因此这棵特定的树正好是二叉树。有的节点也有可能只有一个儿子，如具有一目的减运算符的情形。在上面的树中，左子树的值是a+(b*c)，右子树的值是((d*e)+f)*g，整棵树的表示(a+(b*c))+(((d*e)+f)*g)。

对于上面的二叉树，我们可以通过递归产生一个带括号的左表示式，然后打印出在根处的运算符，最后在递归的产生一个带括号的右表达式进而得到一个中缀表达式。这样一般的方法称为中缀表达式，由于其产生的表达式类型，这种遍历很容易记住。

我们也可以通过后序遍历的方式，得到表达式的后缀表达式。

 

构造一颗表达式树

下面我们给出一种算法，来把表达式的后缀表示转化为表达式树。对于将中缀表达式转换为后缀表达式的算法，我们可以通过栈进行实现。对于构建表达式树的算法：我们一次一个符号的读入表达式，如果符号是操作数，那么我们就建立一个单节点数并将一个指向它的指针推入栈，如果符号是操作符，那么我们就从栈中弹出指向两棵树T1和T2的那两个指针并形成一颗新的数，该树的根就是操作符，它的左，右儿子分别指向T2和T1。然后将指向这棵树的指针压入栈中。

 

查找树ADT——二叉查找树

二叉树的一个重要的应用就是查找。假设树中的每个节点被指定一个关键字值。在我们的例子中，虽然任意复杂的关键字都是可以的，但是为了简单起见，假设它们都是整数。我们还将假设，所有字是互异的，后面再处理重复的情况。

使得二叉树成为二叉查找树的性质是：对于树中的每个节点X，它的左子树中所有关键字值都小于X的关键字值，而它的右子树中所有关键字值大于X的关键字值。

二叉查找树的平均深度是O(logN)。

 

二叉查找树的声明和MakeEmpty

struct TreeNode
typedef struct TreeNode *Position;
typedef struct TreeNode *SearchTree;

struct TreeNode{
　　ElementType Element;
　　SearchTree Left;
　　SearchTree Right;
};

SearchTree
MakeEmpty(SearchTree T){
　　if(T != NULL){
　　　　MakeEmpty(T->Left);
　　　　MakeEmpty(T->Right);
 　　free(T);
　　}
　　return NULL:
}

 

Find

find操作一般是需要返回具有关键字节点的指针，如果节点不存在则返回NULL。如果T为NULL，那么我们就返回NULL。否则，如果存储在T中的关键字是X，则返回T。否则，我们递归的调用遍历左子树或者右子树，这取决于当前节点和X之间的关系。

下面的代码是通过递归进行实现的，我们发现函数中的两次递归都是尾递归，很明显可以通过goto进行实现。但是在这里进行尾递归也是合理的，降低速度换的代码的简明性，并且使用得栈空间也是O(logN)。

Position
Find(ElementType X, SearchTree T){
　　if(T == NULL)
　　　　return NULL;
　　if(X < T->Element){
　　　　Find(X, T->Left);
　　}else if(X > T->Element){
　　　　Find(X, T->Right);
　　}else{
　　　　return T;
　　}
}

 

FindMin 和 FindMax

这些例程分别是返回树中最小值和最大值的位置。返回这些元素的准确值似乎更合理，但是这将与Find操作不相容。FindMin操作只需要从根节点开始不断向左进行，终止点就是最小值。FindMax操作则是相反即可。

下面分别使用递归和非递归编写实现：

递归实现FindMin：

Position
FindMin(SearchTree T){
　　if(T == NULL)
　　　　return NULL;
　　else if(T->Left == NULL)
　　　　return T;
　　else
　　　　return FindMin(T->Left);
}

 

FindMax的非递归操作

Position
FindMax(SearchTree T){
　　if(T != NULL)
　　　　while(T->Right != NULL)
　　　　　　T = T->Right;
　　return T；
}

 

Insert进行操作在例程上面是简单的，为了将X插入树中，我们可以像用Find那样沿着树进行查找。如果找到X，则什么也不做(或做一些更新)。否则，将X插入到遍历路径上面的最后一点。

重复元的插入可以通过在节点记录中保留一个附加于以指示发生的频率处理，不过这将会使得树整体空间增加，但是却比将重复信息放到树中要好(它将使树的深度增加)。当然，如果关键字只是一个更大结构的一部分，那么这种方法行不通。此时我们可以把具有相同关键字的所有结构保留在一个辅助数据结构中，如表或者另一颗查找树中。

下面是插入例程代码：

SearchTree
Insert(ElementType X, SearchTree T){
　　if(T == NULL){
　　　　T = malloc(sizeof(struct TreeNode));
　　　　T->Element = X;
　　　　T->Left = T->Right = NULL;
　　}else if(X < T->Element){
　　　　T->Left = Insert(X, T->Left);
　　}else if(X > T->Element){
　　　　T->Right = Insert(X, T->Right);
　　}
　　return T;
}

 

Delete操作

就像许多数据结构一样，最困难的操作删除。一旦发现要删除节点，我们需要考虑几种可能的情况。

如果节点是一片树叶，那么它可以被立即删除。如果节点有一个儿子，则该节点可以在其父节点调整指针绕过该节点后删除(为了清楚起见，下面给出示意图)

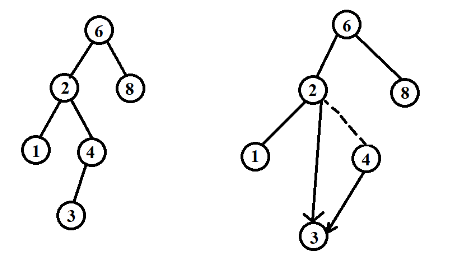
复杂的情况是处理具有两个儿子的节点。一般的删除策略是用其右子树的最小数据代替该节点的数据并且递归删除那个节点。因为右子树的最小节点不可能有左儿子，所以第二次删除要更容易。下面是删除的示意图：

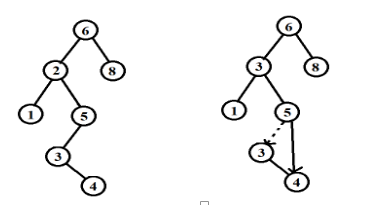
上面所示的程序完成的效率不高，因为它沿着该树进行了两趟搜索来查找和删除右子树最小的节点。可以写一个DeleteMin函数来进行改变效率。

如果删除次数不多，则通常使用的策略是懒惰删除，但一个元素要被删除时，它会仍然留在树中，而是只做一个被删除的记号。这种做法特别是在有重复关键字时很流行，因为此时记录出现的频数的域可以减1。如果树中实际节点数和被删除节点数相同，那么树的深度预计只上升一个小的常数。因此，存在一个与懒惰删除相关的非常小的时间损耗。再有，如果被删除的关键字要重新插入，就可以避免分配空间的消耗。

平均情形分析

直观上，除MakeEmpty外，我们期望前一节所有操作都花费O(logN)时间，因为我们用常数时间在树中降低了一层，这样一来，对树的操作大致减少一半左右。因此，除了MakeEmpty外，所有操作都是O(d)，其中d是包含说访问的关键字的节点深度。

SeachTree Delete(ElementType X, SearchTree T){
　　Position TmpCell;
　　if(T == NULL)
　　　　Error();
　　else if(X < T->Element)
　　　　T->Left = Delete(X, T->Left);
　　else if(X > T->Element)
　　　　T->Right = Delete(X, T->Right);
　　else if(T->Left && T->Right){
　　　　TmpCell = FindMin(T->Right);
　　　　T->Element = TmpCell->Element;
　　　　T->Right = Delete(T->Element, T->Right);
　　}else{
　　　　TmpCell = T;
　　　　if(T->Left == NULL)
　　　　　　T = T->Right;
　　　　else if(T->Right == NULL)
　　　　　　T = T->Left;
　　　　free(TmpCell);
　　}
　　return T;
}

 

下面要证明，假设所有的树出现的机会均等，则树的所有节点的平均深度为O(logN)。

一棵树的所有节点的深度的和称为内部路径长。我们现在将要计算二叉查找树平均内部路径长，其中的平均是对向二叉查找树中所有可能的插入序列进行的。

令D(N)是具有N个节点的某棵树T的内部路径长，D(1)=0。一棵N节点树是由一棵i节点左子树和一棵(N-i-1)节点右子树以及深度为0的一个根节点组成的，其中0<=i<N，D(i)为根的左子树的内部路径长。但是在原树中，所有这些节点都要加深一度。同样的结论对于右子树也是成立的。因此我们得到递归关系：

D(N) = D(i) + D(N - i - 1) + N - 1

如果所有的子树的大小都是等可能出现，这对于二叉查找树是成立的(因为子树的大小只依赖于第一个插入树中的元素的相对的秩),但是对于二叉树不成立。那么，D(i)和D(N-i-1)的平均值都是：

通过求解这个递归关系，得到平均值为D(N)=O(NlogN)。因此任意节点的期望深度为O(logN)。

但是，上来就断言这个结果并不意味着上一节讨论的所有操作的平均运行时间是O(logN)并不完全正确。原因就在于删除操作，我们并不清楚是否所有的二叉查找树都是等可能的出现的。

特别的，上面描述的删除算法有助于左子树比右子树深，因为我们总是用右子树的一个节点来代替删除的节点。已经证明，我们在交替插入和删除大量次数之后，树的期望深度将会变成O(sqrt(N))，树会变得明显的不平衡。

在删除的操作中，我们可以通过随机选取右子树的最小元素或左子树的最大元素来代替被删除的元素以消除这种不平衡。这样能够明显的消除树的偏向并使树保持平衡。

在没有删除或是使用懒惰删除的情况下，可以证明所有的二叉查找树都是等可能的，所以可以断言：上述的操作都是O(logN)的时间复杂度。

另外比较新的方法是放弃平衡条件，允许树有任意的深度，但是每次操作时候使用一个规则进行调整，使得后面的操作效率更高。

 

AVL树

AVL树是带有平衡条件的二叉查找树。这个平衡条件必须容易保持，而且能够保证树的深度是O(logN)。最简单的想法是要求左右子树具有相同的高度。

另一种平衡条件是要求每个节点都必须要有相同高度的左右子树。这个平衡条件虽然保证树的深度小，但是太过于严格，难以使用。

AVL树是其每个节点的左子树和右子树的高度最多差1的二叉查找树。(空树的高度定义为-1)。一颗AVL树的高度最多是1.44log(N+2)-1.328，但是实际上高度只是比logN稍微多一点点。

在高度为h的AVL树中，最少节点数S(h)由S(h)=S(h-1)+S(h-2)+1给出。对于h=0，S(h)=1;h=1,S(h)=2。函数S(h)与斐波那契密切相关,由此推出上面的AVL树的高度的界。

当进行插入时，我们需要更新通向根节点路径上面的那些节点的所有平衡信息，插入操作的困难在于，插入一个节点可能会破坏AVL树的特性。发生这种情况，就需要对树进行恢复以后才算完成插入操作。事实上，可以通过对树进行旋转来完成。

插入节点以后，只有从插入点到根节点的路径上的节点的平衡可能改变，因为只有这些节点的子树可能发生变化。当我们沿路径上行到根并且更新节点平衡信息时，我们可以找到一个节点，它的平衡破坏了AVL条件。我们将指出如何在第一个这样的节点重新平衡这个树，并证明，这一重新平衡保证整个书满足AVL特性。

如果把重新平衡的节点叫做a。由于任意节点最多有两个儿子，因此高度不平衡时，a点的两棵子树的高度差2，易知，不平衡出现在下面的四种情况中：

1.对a的左儿子的左子树进行一次插入

2.对a的左儿子的右子树进行一次插入

3.对a的右儿子的左子树进行一次插入

4.对a的右儿子的右子树进行一次插入

情况1和4是关于a点的镜像对称，2和3是关于a点的镜像对称。

第一种情况是插入发生在外边，即左-左或右-右的情况，该情况通过对树进行一次单旋转而完成调整。第二种情况是发生在内部的情形，即左-右或者右-左的情况，该情况会稍微复杂一些通过双旋转进行调整。

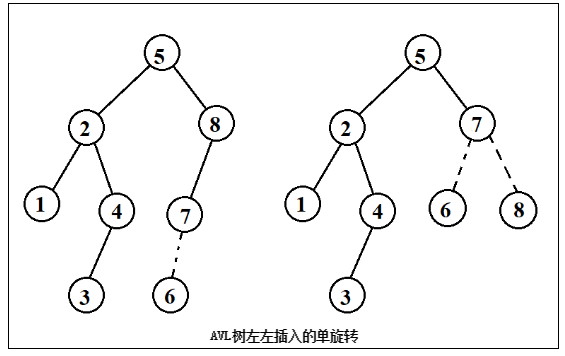
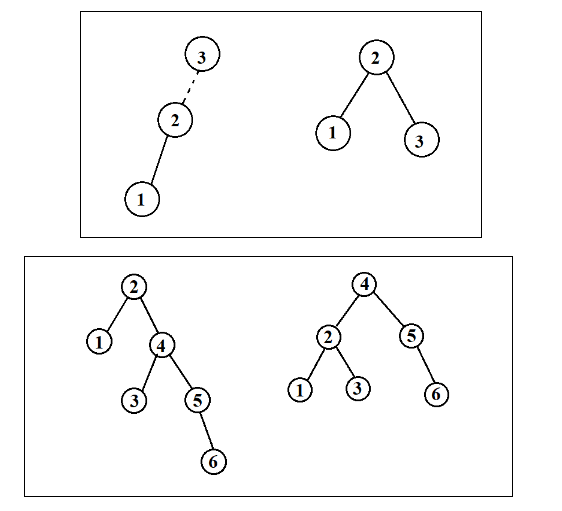
双旋转

对于右左插入或者左右插入的情况，是无法通过单旋转进行解决的，需要进行双旋转来解决。

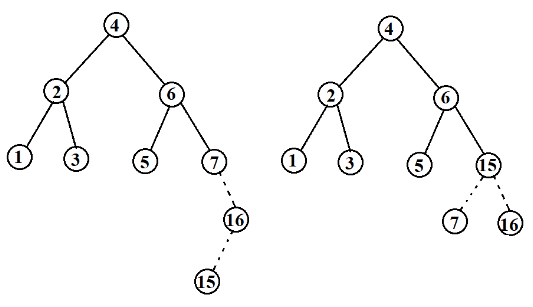
现在让我们对上面的讨论做个总结。除几种情形外，为将关键字X插入一颗AVL树中，我们递归的将X插入到T对应的树中。如果TLR的高度不变，那么就插入完成。否则，如果在T中出现不平衡，那么我们根据X以及T和TLR中的关键字做适当的单旋转或者双旋转，更新这些高度，并解决好与树的其余部分的连接，从而完成一次插入。

另一种效率问题设计到高度的存储。真正需要存储的是子树的高度，应该保证它很小，我们可以用两个二进制位来进行存储。

struct AvlNode;
typedef struct AvlNode *Position;
typedef struct AvlNode *AvlTree;

struct AvlNode{
　　ElementType Element;
　　AvlTree Left;
　　AvlTree Right;
　　int Height;
};

对于AVL树的删除多少要比插入复杂。如果删除操作相对较少，那么懒惰删除恐怕是最好的策略。

计算节点的高度

static int
Height(Position P){
　　if(P == NULL){
　　　　return -1;
　　}else{
　　　　return P->Height;
　　}
}

向AVL树中插入节点的函数

AvlTree Insert(ElementType X, AvlTree T){
　　if(T == NULL){
　　　　T = malloc(sizeof(struct AvlNode));
　　　　if(T == NULL)
　　　　　　return ERROR();
　　　　T->Element = X; T->Height = 0;
　　　　T->Left = T->Right = NULL;
　　}else if(X < T->Element){
　　　　T->Left = Insert(X, T->Left);
　　　　if(Height(T->Left) - Height(T->Right) == 2)
　　　　　　if(X < T->Left->Element)
　　　　　　　　T = SingleRotateWithLeft(T);
　　　　　　else
　　　　　　　　T = DoubleRotateWithLeft(T); 
　　}else if(X > T->Element){
　　　　T->Right = Insert(X, T->Right);
　　　　if(Height(T->Right) - Height(T->Left) == 2)
　　　　　　if(X > T->Right->Element)
　　　　　　　　T = SingleRotateWithRight(T);
　　　　　　else
　　　　　　　　T = DoubleRotateWithRight(T);
　　}
　　T->Height = Max(Height(T->Left), Height(T->Right)) + 1;
　　return T;
}

static Position SingleRotateWithLeft(Position K2){
　　Position K1; 
　　K1 = K2->Left;
　　K2->Left = K1->Right;
　　K1->Right = K2;
　　K2->Height = Max(Height(K2->Left), Height(K2->Right)) + 1;
　　K1->Height = Max(Height(K1->Left), K2->Height) + 1;
　　return K1;
}

static Position DoubleRitateWithLeft(Position K3){
　　K3->Left = SingleRotateWithRight(K3->Left);
　　return SingleRotateWithLeft(K3);
}

 

树的遍历

对于二叉树的遍历而言，由于每个节点工作花费的时间以及总共有N个节点，因此总的运行时间是O(N)。

树的遍历可以分为前序遍历，中序遍历，后序遍历和层次遍历。对于树的层次遍历，我们使用队列进行辅助，而不是递归默认的栈。

 

B-树

B-树是一种常用的查找树，阶为M的B树具有下列的结构特性：

• 树的根或者是一片树叶，或者是其儿子数在2和M之间

• 除根外，所有非树节点的儿子数在[M/2]和M之间

• 所有的树叶都在相同的深度上

所有的数据都存储在树叶上，在每一个内部的节点上皆含有指向该节点个儿子的指针P1,P2，......，Pm和分别代表在子树P2,P3，......,Pm中发现的最小关键字的值K1，K2，......,km-1。当然可能有指针是NULL，而其对应的Ki则是未定义的。对于每一个节点，其子树P1中的关键字都小于子树P2的关键字，如此等等。

树叶包含所有的实际数据，这些数据或者是关键字本身，或者是指向含有关键字的记录的指针。

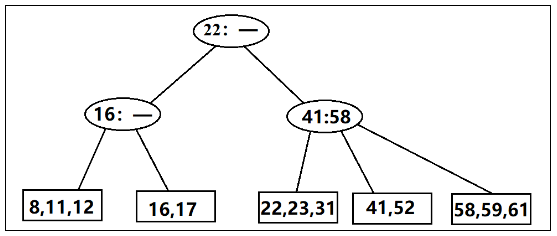
对于一棵阶为M的B树的性质：

　　树的根或者是一片叶子，或者是儿子数在2和M之间

　　除根外的，非树叶子节点的儿子数在M/2(向上取整)和M之间

　　所有的树叶都在相同的深度上

　　所有的数据都存储在叶子上

　　每个内部节点皆含有指向各个儿子的指针和分别代表非首节点的最小关键值的值

　　对于每个节点其子树P1中所有的关键值都小于子树P2的关键字

对于B的的Insert操作，先按照Find()操作进行，当到达树叶时，就找到了插入X的正确的位置。当树叶的单元不够存储时，我们需要进行一系列的操作调整。

对于一般的M阶B树，当插入一个关键字，唯一的的困难发生在接收该关键字的节点已经有M个关键字的时候。这个关键字使得该节点具有M+1个关键字。我们可以把它分成两个节点，它们分别具有(M+1)/2个和(M+1)/2个关键字。由于这使得父节点多出一个儿子，因此需要检查这个节点是否可被父节点接收，如果父节点已经具有M个儿子，那么父节点就要被分裂成两个节点。我们重复这个过程，直到找到一个父节点至少M个儿子。如果我们分裂根节点，我们就要创建一盒新的根，这个根有两个儿子。

B树的深度最多是[log(M/2)N]。在路径上的每个节点，我们执行O(logM)时间的工作量以确定选择哪个分子。

下面是一个AVL的例程：

 

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
using namespace std;

typedef int Height;
typedef int Element;
typedef struct AVLTree;
typedef AVLTree* Tree;


struct AVLTree{
    Element element;
    Tree left;
    Tree right;
    Height height;
    AVLTree(Element x):element(x), left(NULL), right(NULL), height(0){};
};

int max(int a, int b){
    return a > b ? a : b;
}


Tree makeEmpty(Tree t){
    if(t != NULL){
        makeEmpty(t->left);
        makeEmpty(t->right);
        delete(t);
    }
    return NULL;
}


Height getHeight(Tree t){
    if(t == NULL){
        return -1;
    }else{
        return t->height;
    }
}


Tree singleRotateLeft(Tree t){
    Tree p;
    p = t->left;
    t->left = p->right;
    p->right = t;
    t->height = max(getHeight(t->left), getHeight(t->right)) + 1;
    p->height = max(getHeight(p->left), t->height) + 1;
    return p;
}


Tree singleRotateRight(Tree t){
    Tree p;
    p = t->right;
    t->right = p->left;
    p->left = t;
    t->height = max(getHeight(t->left), getHeight(t->right)) + 1;
    p->height = max(t->height, getHeight(p->right)) + 1;
    return p;
}


Tree doubelRotateLeft(Tree t){
    t->left = singleRotateRight(t->left);
    return singleRotateLeft(t);
}

Tree doubelRotateRight(Tree t){
    t->right = singleRotateLeft(t->right);
    return singleRotateRight(t);
}


Tree insertNode(Tree t, Element x){
    if(t == NULL){
        t = new AVLTree(x);
    }else if(x < t->element){
        t->left = insertNode(t->left, x);
        if(getHeight(t->left) - getHeight(t->right) == 2){
            if(x < t->left->element){
                t = singleRotateLeft(t);
            }else{
                t = doubelRotateLeft(t);
            }
        }
    }else if(x > t->element){
        t->right = insertNode(t->right, x);
        if(getHeight(t->right) - getHeight(t->left) == 2){
            if(x < t->right->element){
                doubelRotateRight(t);
            }else{
                singleRotateRight(t);
            }
        }
    }
    t->height = max(getHeight(t->left), getHeight(t->right)) + 1;
    return t;
}


void inPrinter(Tree t){
    if(t == NULL){
        return;
    }else{
        inPrinter(t->left);
        printf("%d  %d\n", t->element, t->height);
        inPrinter(t->right);
    }
}

int main(){
    Tree t = NULL;
    t = makeEmpty(t);
    t = insertNode(t, 5);
    t = insertNode(t, 2);
    t = insertNode(t, 8);
    t = insertNode(t, 1);
    t = insertNode(t, 4);
    t = insertNode(t, 7);
    t = insertNode(t, 3);
    inPrinter(t);
    printf("\n==========================\n");
    // t = insertNode(t, 6);
    printf("\n==========================\n");
    // inPrinter(t);
    // t = insertNode(t, 1);
    // t = insertNode(t, 1);


}