机器学习——logistic回归，鸢尾花数据集预测，数据可视化

0.鸢尾花数据集

　　鸢尾花数据集作为入门经典数据集。Iris数据集是常用的分类实验数据集，由Fisher, 1936收集整理。Iris也称鸢尾花卉数据集，是一类多重变量分析的数据集。数据集包含150个数据集，分为3类，每类50个数据，每个数据包含4个属性。可通过花萼长度，花萼宽度，花瓣长度，花瓣宽度4个属性预测鸢尾花卉属于（Setosa，Versicolour，Virginica）三个种类中的哪一类。

　　在三个类别中，其中有一个类别和其他两个类别是线性可分的。另外。在sklearn中已内置了此数据集。

from sklearn.datasets import load_iris #导入IRIS数据集 
iris = load_iris()  #特征矩阵

　　数据集的格式如下图所示：

 

1.数据集的载入

　　虽然在sklearn中，内置了鸢尾花数据集，但是我们用的是下载好的数据集，下面是数据集的读入，我们先通过手动的方式将数据集进行读入。

f = open(path)
x = []
y = []
for d in f:
    d = d.strip()
    if d:
        d = d.split(',')
        y.append(d[-1])
        x.append(list(map(float, d[:-1])))
x = np.array(x)
y = np.array(y)
print(x)
y[y == 'Iris-setosa'] = 0
y[y == 'Iris-versicolor'] = 1
y[y == 'Iris-virginica'] = 2
print(y)
y = y.astype(dtype=np.int)
print(y)

　　代码的13-15中，通过判断y中的标签值，返回的是一个y大小相同的一个boolearn类型的列表，在通过这个列表进行赋值操作，非常的迅速和灵活。

　　读取的X数据如下：

 

　　处理后的标签的数据如下：

　　除了上述方式的手动读入数据，还可以通过pandas库来进行数据的读取。

import numpy as np
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn import preprocessing
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline

df = pd.read_csv(path, header=0)
x = df.values[:, :-1]
y = df.values[:, -1]
print('x = \n', x)
print('y = \n', y)
le = preprocessing.LabelEncoder()
le.fit(['Iris-setosa', 'Iris-versicolor', 'Iris-virginica'])
print(le.classes_)
y = le.transform(y)
print('Last Version, y = \n', y)

　　上述代码中，pd.read_csv(path, header=0)，header ：指定行数用来作为列名，数据开始行数。如果文件中没有列名，则默认为0【第一行数据】，否则设置

为None。

 　　sklearn.preprocessing.LabelEncoder()：标准化标签，将标签值统一转换成range(标签值个数-1)范围内，例如["paris", "paris", "tokyo", "amsterdam"]；里面不

同的标签数目是3个，则标准化标签之后就是0，1，2，并且根据字典排序。

 　　le.fit(['Iris-setosa', 'Iris-versicolor', 'Iris-virginica'])含义为将标签集喂给le标签处理器，y = le.transform(y)对y进行转化。

　　也可以使用numpy来对数据进行加载。

def iris_type(s):
    it = {b'Iris-setosa': 0, b'Iris-versicolor': 1, b'Iris-virginica': 2}
    return it[s]

data = np.loadtxt(path, dtype=float, delimiter=',', converters={4: iris_type})

　　使用np中的loadtxt来对数据加载，delimiter指定数据的分割符，converter为指定需要进行转换的列及对应的转换函数。

 

2.构建线性模型

　　为了后面的可视化的效果，我们在此仅选用了连两个特征构建logistic回归模型，代码如下：　

x = x[:, :2] 
print(x)
print(y)
x = StandardScaler().fit_transform(x)
lr = LogisticRegression()   # Logistic回归模型
lr.fit(x, y.ravel())        # 根据数据[x,y]，计算回归参数

　　StandardScaler----计算训练集的平均值和标准差，以便测试数据集使用相同的变换。即fit_transform()的作用就是先拟合数据，然后转化它将其转化为标准形

式。调用fit_transform()，其实找到了均值μ和方差σ^2，即已经找到了转换规则，把这个规则利用在训练集上，同样，可以直接将其运用到测试集上（甚至交叉验证

集）。

　　我们也可以使用管道的方式构建模型，并进行训练：

lr = Pipeline([('sc', StandardScaler()),
                    ('clf', LogisticRegression()) ])
lr.fit(x, y.ravel())

　　LogisticRegression()的主要参数如下：

• penalty：惩罚项，str类型，可选参数为l1和l2，默认为l2。用于指定惩罚项中使用的规范。newton-cg、sag和lbfgs求解算法只支持L2规范。L1规范假设的是模型的参数满足拉普拉斯分布，L2假设的模型参数满足高斯分布。
• dual：对偶或原始方法，bool类型，默认为False。对偶方法只用在求解线性多核(liblinear)的L2惩罚项上。当样本数量>样本特征的时候，dual通常设置为False。
• tol：停止求解的标准，float类型，默认为1e-4。就是求解到多少的时候，停止，认为已经求出最优解。
• c：正则化系数λ的倒数，float类型，默认为1.0。必须是正浮点型数。像SVM一样，越小的数值表示越强的正则化。
• fit_intercept：是否存在截距或偏差，bool类型，默认为True。
• intercept_scaling：仅在正则化项为”liblinear”，且fit_intercept设置为True时有用。float类型，默认为1。
• class_weight：用于标示分类模型中各种类型的权重，可以是一个字典或者’balanced’字符串，默认为不输入，也就是不考虑权重，即为None。
• random_state：随机数种子，int类型，可选参数，默认为无，仅在正则化优化算法为sag,liblinear时有用。
• solver：优化算法选择参数，只有五个可选参数，即newton-cg,lbfgs,liblinear,sag,saga。默认为liblinear。solver参数决定了我们对逻辑回归损失函数的优化方法，有四种算法可以选择，分别是： 
  • liblinear：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。
  • lbfgs：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
  • newton-cg：也是牛顿法家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
  • sag：即随机平均梯度下降，是梯度下降法的变种，和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。
  • saga：线性收敛的随机优化算法的的变重。

　　详细的参数描述传送门

 

3.模型的可视化

　　我们可以在所选特征的范围内，从最大值到最小值构建一系列的数据，使得它能覆盖整个的特征数据范围，然后预测这些值所属的分类，并给它们所在的区域

上色，这样我们就能够清楚的看到模型每个分类的区域了，具体的代码如下所示：

N, M = 500, 500     # 横纵各采样多少个值
x1_min, x1_max = x[:, 0].min(), x[:, 0].max()   # 第0列的范围
x2_min, x2_max = x[:, 1].min(), x[:, 1].max()   # 第1列的范围
t1 = np.linspace(x1_min, x1_max, N)
t2 = np.linspace(x2_min, x2_max, M)
x1, x2 = np.meshgrid(t1, t2)                    # 生成网格采样点
x_test = np.stack((x1.flat, x2.flat), axis=1)   # 测试点

cm_light = mpl.colors.ListedColormap(['#77E0A0', '#FF8080', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
y_hat = lr.predict(x_test)       # 预测值
y_hat = y_hat.reshape(x1.shape)                 # 使之与输入的形状相同
plt.pcolormesh(x1, x2, y_hat, cmap=cm_light)     # 预测值的显示
plt.scatter(x[:, 0], x[:, 1], c=y.ravel(), edgecolors='k', s=50, cmap=cm_dark)    
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.grid()
plt.savefig('2.png')
plt.show()

　　np.meshgrid()函数常用于生成网格数据，多用于绘制三维图形。 mpl.colors.ListedColormap(['#77E0A0', '#FF8080', '#A0A0FF'])生成一个颜色的列表，plt.pcolormesh(x1, x2, y_hat, cmap=cm_light) 根据颜色列表中的值，给传入的坐标进行绘图。

　　绘制的图片的效果如下：

 

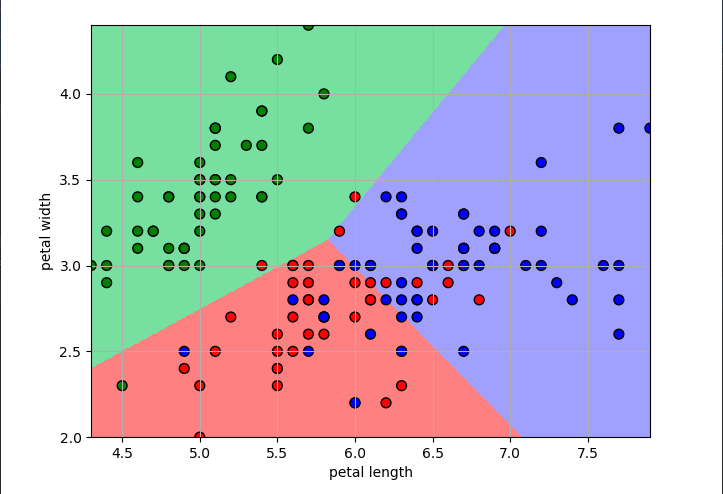
4.计算模型的准确率　

　　由于我们使用的是两个特征进行数据集的分类，所以分类的准确率并不是高，代码如下：

y_hat = lr.predict(x)
y = y.reshape(-1)
result = y_hat == y
print(y_hat)
print(result)
acc = np.mean(result)
print('准确度: %.2f%%' % (100 * acc))

　　具体的准确率是多少呢？同学们可以自己动手试一下哦！

 欢迎关注我的公众号，不定期分享机器学习模型原理！