凸优化，对偶问题与拉格朗日函数

优化问题的基本形式

 

 

 

 

 

 

最大值问题可转化为最小值问题 

 

优化问题的域

　　　　　

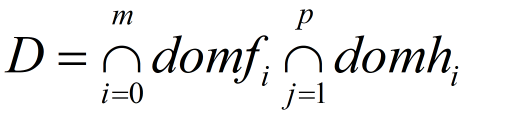
可行域：所有可行点的集合

最优化值：

最优化解：

 

凸优化问题的基本形式

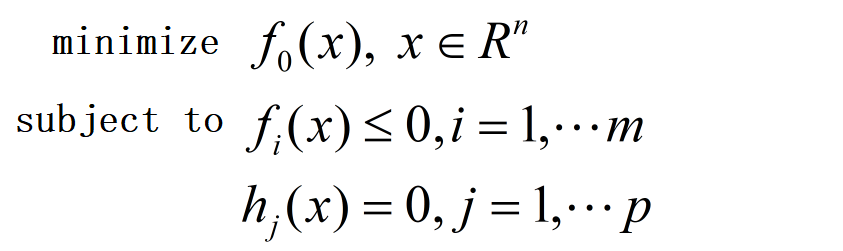
其中，约束函数f(x)是凸函数，h(x)为仿射函数

 仿射函数：即最高次数为1的多项式函数。常数项为零的仿射函数称为线性函数。

 凸优化问题的重要性质：

　　1.凸优化问题的可行域为凸集

　　2.凸优化问题的局部最优解即为全局最优解

 

对偶问题

 一般优化问题的拉格朗日乘子法

　　　　

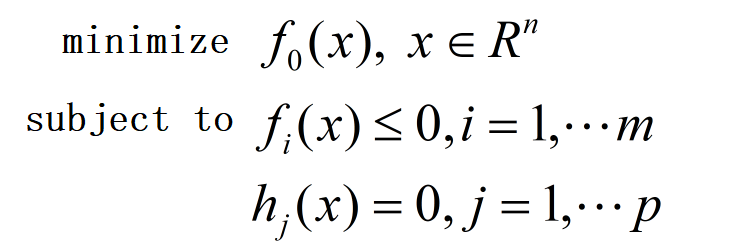
拉格朗日函数

　　　　

对固定的x，拉格朗日函数是关于和的仿射函数，当x为定值时，f(x)为定值，h(x)为定值，函数关于 线性，关于线性，即为若干条直线。

拉格朗日对偶函数

　　　　

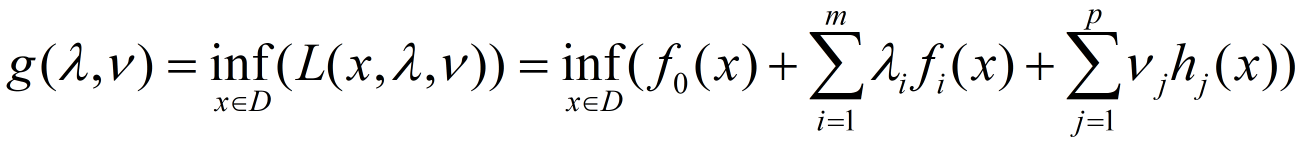
若问题没有明确的下确界，则g(lamta,V) 为负无穷

 　　　　

根据定义，显然有：对于任意的lamda，任意的x，若优化问题有最优值p，则g(lamta,V) <=p

进一步，拉格朗日对偶函数为凹函数

 

分析

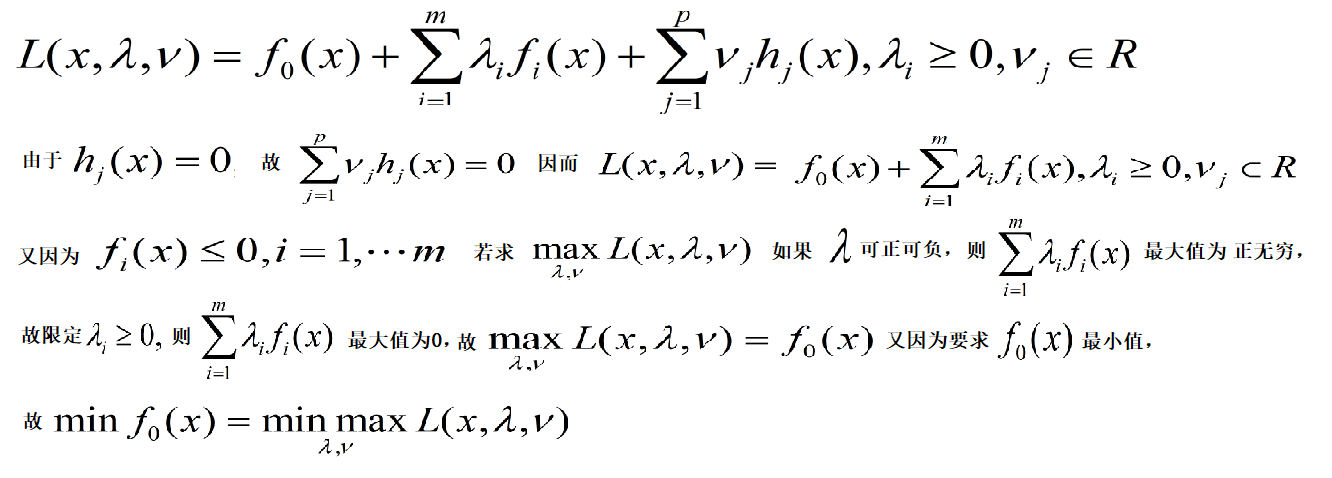
公式纯手打QAQ！

对偶

 

 

 

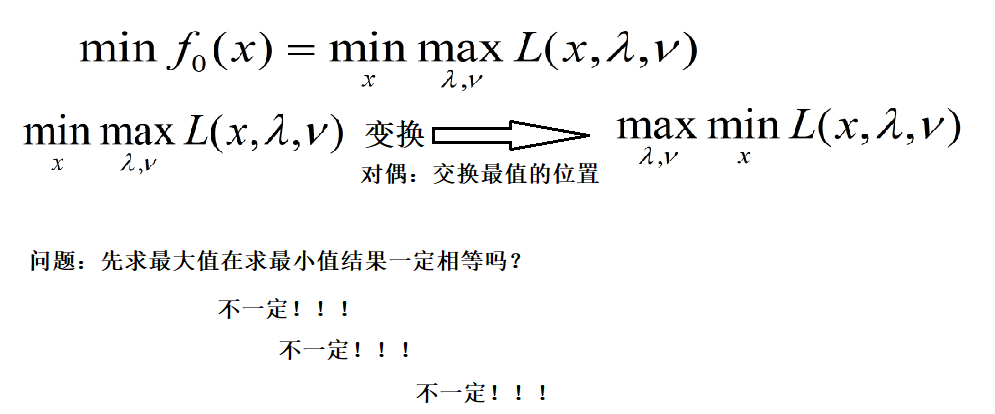
强对偶条件

若要对偶函数的最大值等于原问题的最小值，则需满足：

KKT条件

 

 实践案例

可以参见SVM的求解过程！