机器学习中的凸优化,凸集,凸函数的相关定义和理论
仿射集
定义:通过集合C中任意的两个不同的点的直线仍然在集合C内,则层集合C为仿射集。
![]()
仿射集的例子:直线,平面,超平面
超平面:AX=b
f(x) = 0表示定义在定义域Rn的超平面,令f(x)=Ax-b,则f(x)=0表示“截距”为b的超平面。在三维空间的平面是二维的,四维空间的平面是三维的,n维空间的平面是n-1维的仿射集。
凸集
定义:集合C内的任意取两点,形成的线段均在集合C内,则称集合C为凸集。仿射集一定是凸集。
![]()
扩展到k个点的时候:
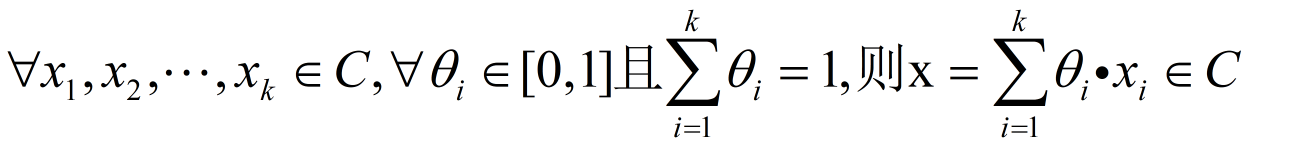
凸集的示例:

凸包
集合C中的所有点的凸组合形成的集合,叫集合的凸包。
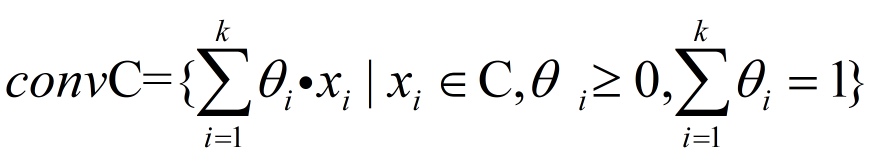
凸包是能够包含集合的最小凸集
示例:

凸函数
y=x**2是凸函数,即函数图像上方的区域能够构成凸集。
凸函数示例:

- 凸函数图像的上方区域,一定是凸集
- 一个函数图像的上方区域为凸集,则该函数是凸函数
凸集和凸函数能够一一对应
凸函数的充要条件:如果函数的二阶导数存在且大于0,则函数为凸函数(很恒大于0)。反之则不成立,所以不是必要条件。

凸函数的性质:
1.若凸函数的f(x)的定义域domf为凸集,且满足:
![]()
几何含义:
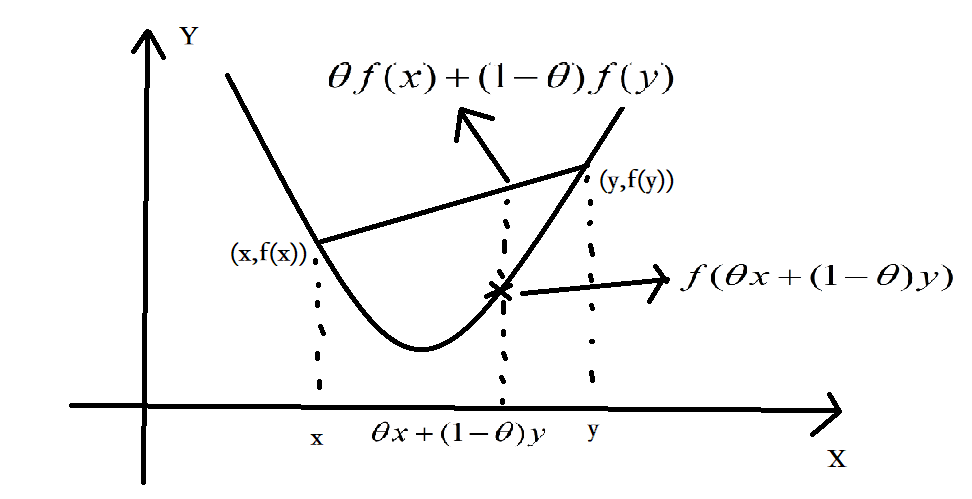
割线位于函数值的上方
一阶可微
若函数f(x)一阶可微,则函数f为凸函数,当且仅当f的定义域为凸集,且:
![]() (支撑超平面)
(支撑超平面)
几何含义:
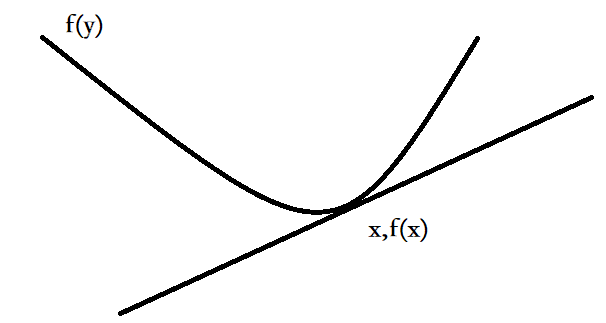
切线在函数的下方
思考:对于凸函数,其一阶taylor近视本质上是该函数的全局下估计,反之,如果一个函数的一阶Taylor近视总是超全局下估计,则该函数是凸函数。该不等式说明从一个函数的局部信息,可以得到一定程度上的全局信息。
二阶可微
若函数f(x)二阶可微,则函数f(x)为凸函数当且仅当dom为凸集,且:
![]()
若f是一元函数,上述式子为二阶导数大于等于0
若f是多元函数,上述式子表示二阶导hessian矩阵半正定
凸函数举例:指数函数,幂函数(指数大于1或者小于0),负对数函数,负熵函数,范数函数,指数线性函数。
Jensen不等式(函数需为凸函数)
基本的Jensen不等式:
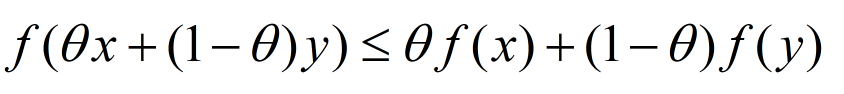
注:当扩展到n元函数时,仍然成立
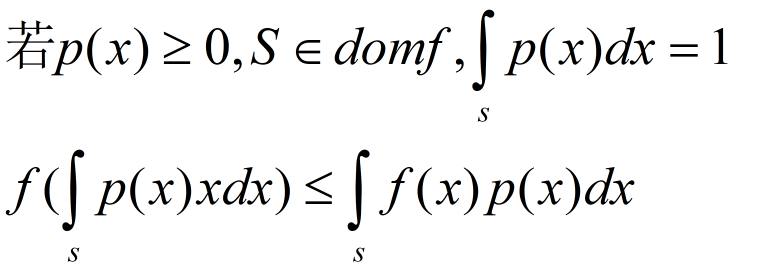
保持函数凸性质的算子
1.凸函数的非负加权和:f(x) = w1f1(x) + w2f2(x) + w3f3(x)
2.凸函数与仿射函数的复合: f(x) = g(ax+b)
3.凸函数的逐点最大值,逐点上确界: f(x) = max{f1(x), f2(x),........},f(x) = sup(x,y)




