图的总结
一.思维导图

二.重要概念的笔记
1.图的分类
图是按照无方向和有方向分为无向图和有向图。
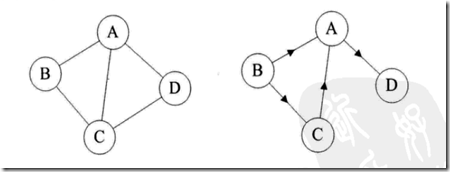
2.图的存储结构
1.邻接矩阵(分有向图和无向图)
邻接矩阵用两个数组保存数据。一个一维数组存储图中顶点信息,一个二维数组存储图中边或弧的信息。
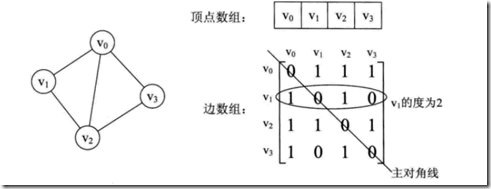
无向图中二维数组是个对称矩阵。
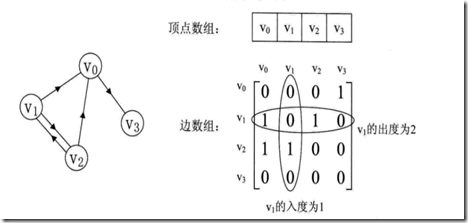
若有权值,则为
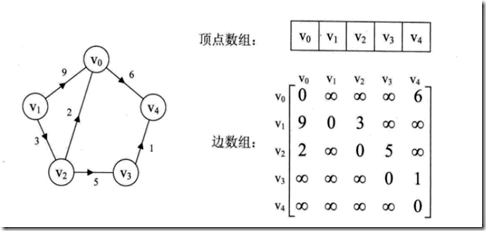
邻接矩阵对于边数相对顶点较少的图,就是对存储空间极大的浪费。
2.邻接表

3.图的遍历
1.深度优先遍历(DFS)
它从图中某个结点v出发,访问此顶点,然后从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到。若图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,直至图中的所有顶点都被访问到为止。
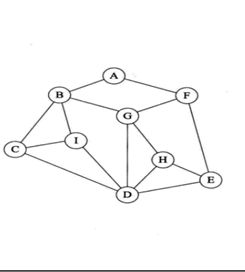
最后得到的访问序列为A→B→C→D→E→F→G→H→I。
2.广度优先遍历(BFS)
从图中的某一个顶点Vi触发,访问此顶点后,依次访问Vi的各个为层访问过的邻接点,然后分别从这些邻接点出发,直至图中所有顶点都被访问到。

最后得到的访问序列为A→B→F→C→I→G→E→D→H。
4.最小生成树
1.普利姆(Prim)算法(时间复杂度为O(n^2))
1.从一个节点(随便选一个)开始,去找这个节点相邻最短的边
2.将找到的边添加到这个节点上,这就形成一个组件了
3.再从这个组件开始去找相邻权重最小的边,再添加到这个组件上,不断重复直到所有节点都能被访问
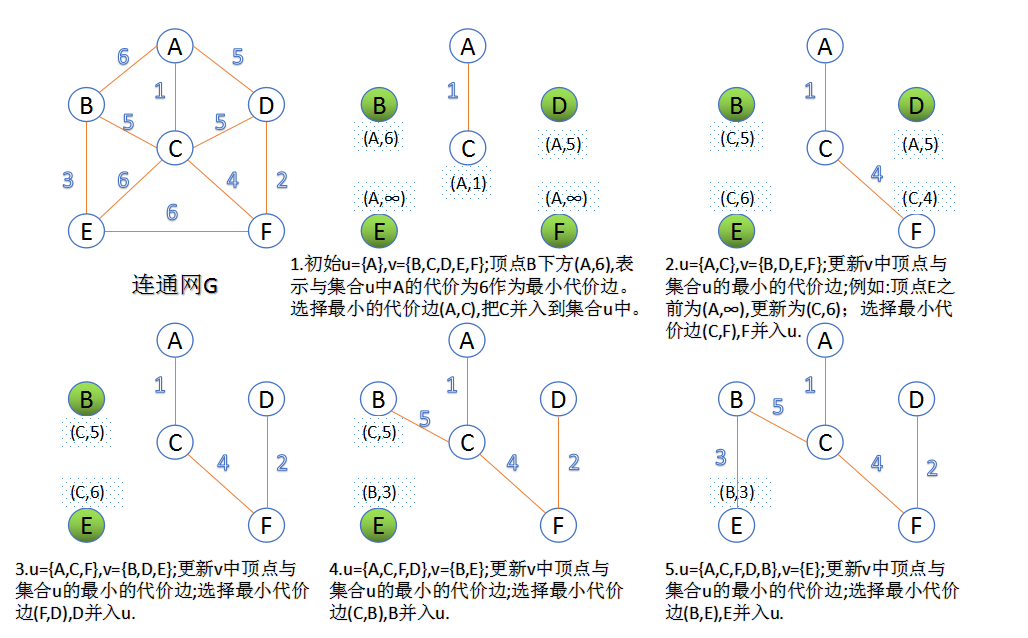
2.克鲁斯卡尔(Kruskal)算法(时间复杂度为O(eloge))
1.首先获取所有的边,都这些边进行从小到大的排序
2.然后不断往图里添加边,并且避免造成环
3.直到所有点都能互相访问后停止算法
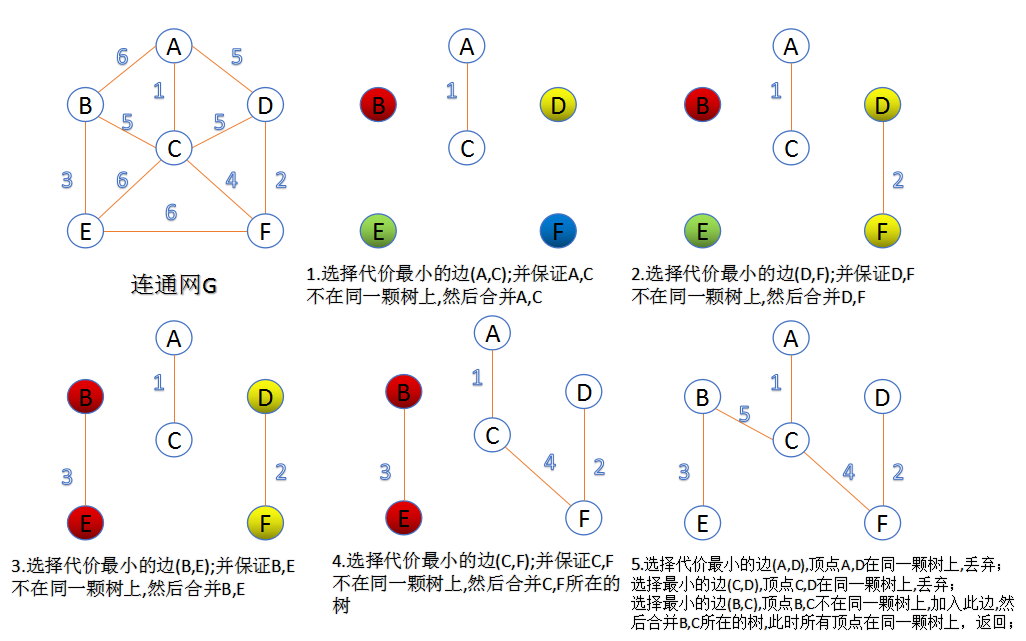
5.拓扑排序
1.从AOV网络中删除入度为0的顶点;有入度这个概念,则用链表的存储结构储存数据。
2.删除此顶点还有顶点尾的弧;此时删除顶点(输出数据),删除顶点为尾的弧,意味这弧消失,图中一个顶点的入度减1.必须在顶点表中有表示度的变量。
3.继续循环,直到不存在度为0的顶点;就是循环停止条件是顶点全部输出。
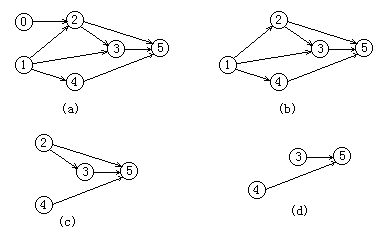
6.Dijkstra(迪杰斯特拉)算法
1.创建顶点结合nNodeIndex,初始化为0,数组中为1是,表示对应的顶点已经添加到最短路径顶点集合S了。
2.创建初始顶点到各个顶点的边集合,保存此顶点到各个顶点的距离(权重),用邻接矩阵中行元素初始化(类似最小生成树)。
3.循环计算此顶点到各个顶点的最小值,得知后nNodeIndex[i] = 1,同时更新边集合 的数值。
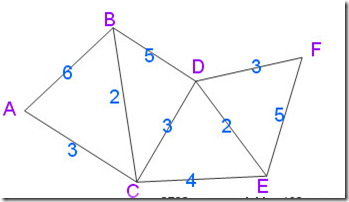
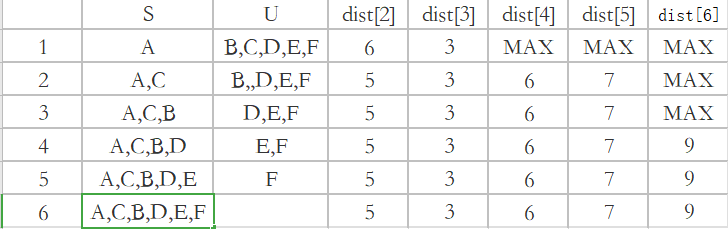
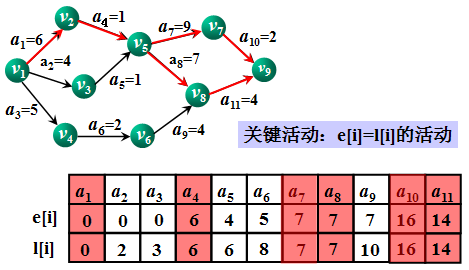
7.关键路径
1.事件最早发生时间ve:顶点vk的最早发生时间,从始点到vi的最长(加权)路径长度。
2.事件最晚发生时间vl:顶点vk的最晚发生时间,在不拖延整个工期的条件下,vi的可能的最晚发生时间。。
3.活动最早发生时间e:活动ak的最早发生时间,等于事件vi的最早发生时间。
4.活动最晚发生时间l:弧ak的最晚发生时间,在不拖延整个工期的条件下,该活动的允许的最迟开始时间。
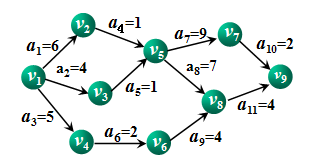
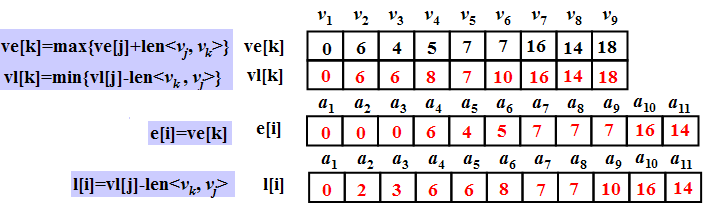
三.疑难问题及解决方法
7-1 图着色问题 (25分)

#include<iostream>
#include<memory.h>
using namespace std;
struct Graph
{
int a[501][501];
int v,e;
};
int z,visited[501]={0},d[501],k=0,n,i,j;
Graph *creat()
{
Graph *g=new Graph;
int x,y,i;
memset(g->a,0,sizeof(g->a));
cin>>g->v>>g->e>>z;
for(i=0;i<g->e;i++)
{
cin>>x>>y;
g->a[x][y]=g->a[y][x]=1;
}
return g;
}
void dfs(Graph *g,int i)
{
int j;
d[k++]=i;
visited[i]=1;
for(j=1;j<=g->v;j++)
{
if(g->a[i][j]==1 && visited[j]==0) dfs(g,j);
}
}
void dfs1(Graph *g)
{
int i;
for(i=1;i<=g->v;i++)
{
if(visited[i]==0) dfs(g,i);
}
}
int main()
{
Graph *g=creat();
dfs1(g);
cin>>n;
while(n--)
{
int b[501]={0},c[501],e[501],sum=0,flag=1;
for(i=1;i<=g->v;i++)
{
cin>>c[i];
b[c[i]]++;
if(b[c[i]]==1) sum++;
}
if(sum!=z) flag=0;
for(i=0;i<k;i++) e[i]=c[d[i]];
for(i=0;i<k;i++)
{
for(j=0;j<k;j++)
{
if(g->a[d[i]][d[j]]==1 && e[i]==e[j])
{
flag=0;
break;
}
}
if(flag==0) break;
}
if(flag==0) puts("No");
else puts("Yes");
}
return 0;
}
本题一开始看完题目并不能很好的理解,在询问同学以及老师的讲解后,最后做了出来。



