树，二叉树，查找算法总结

一.思维导图

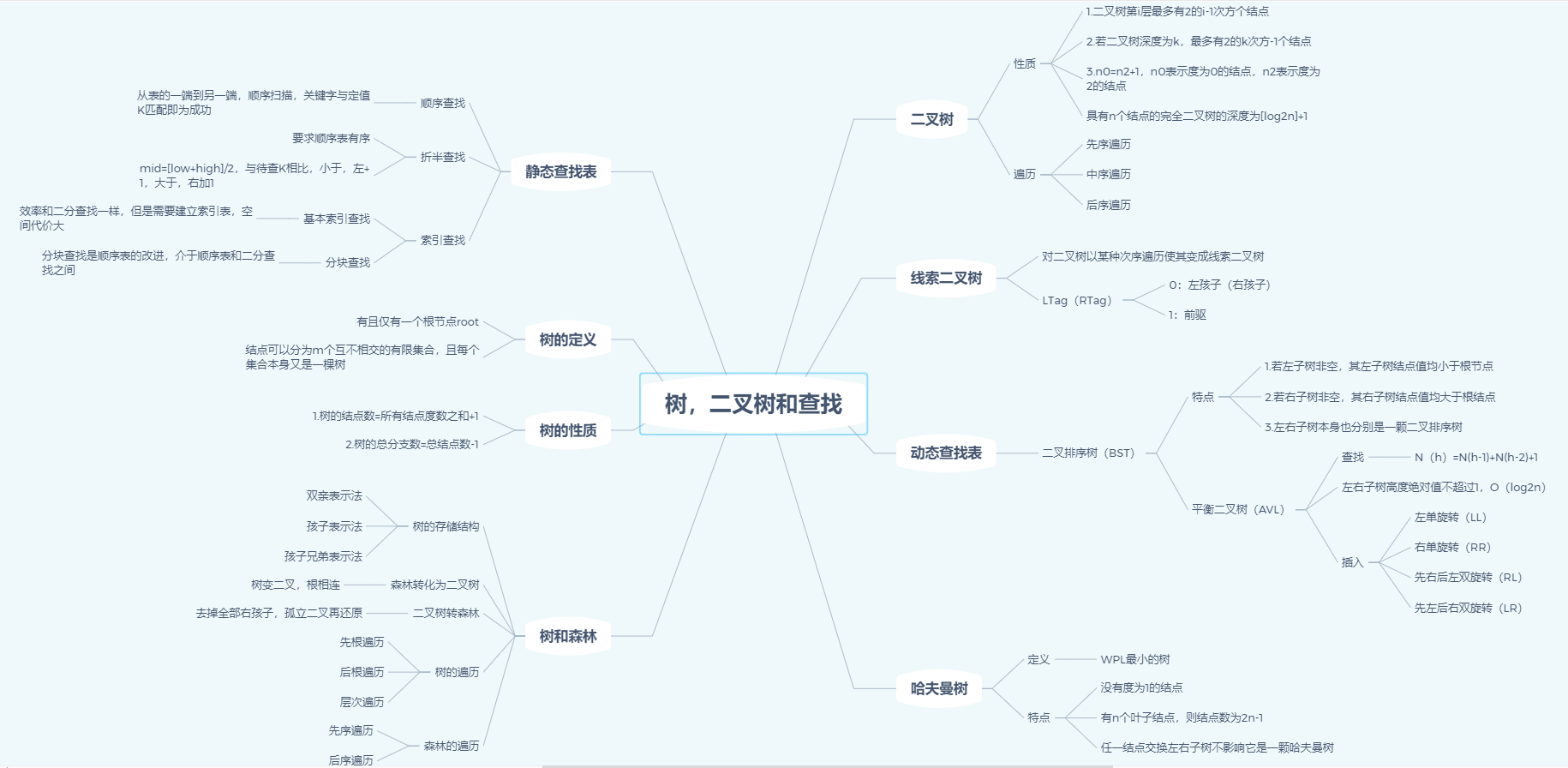
二.重要概念的笔记

1.一般树的存储：

1.双亲表示法：求父节点方便。
2.孩子表示法：求子节点方便。
3.双亲孩子表示法：求父节点和子节点都很方便。
4.二叉树表示法：将一颗普通树转化为二叉树。

2.二叉树的性质：

1.在二叉树的第i层上至多有2^(i-1)个结点（i>0）。
2.深度为k的二叉树至多有2^k-1个结点（k>0）。
3.对于任意一棵二叉树，如果其叶结点为N0，而度数为2的结点总数为N2，则N0=N2+1。
4.具有n个结点的完全二叉树的深度必为 log（2n）+1。
5.对完全二叉树，若从上至下、从左只右编号，则编号为i的节点，其左孩子编号必为2i，其有孩子编号必为2i+1；其双亲的编号必为i/2（i=1时为根 除外）。

3.折半查找的时间复杂度为：O(log2n)。

4.B树：

1、概念：
它或者是一棵空树；或者是具有下列性质的二叉树：
(1)若左子树不空，则左子树上所有结点的值均小于左子树所在树的根结点的值；
(2)若右子树不空，则右子树上所有结点的值均大于右子树所在树的根结点的值；
(3)左、右子树也分别为二叉排序树；
2、B树的查找：
时间复杂度与树的深度的有关。
步骤：若根结点的关键字值等于查找的关键字，成功。
否则：若小于根结点的关键字值，递归查左子树。
若大于根结点的关键字值，递归查右子树。
若子树为空，查找不成功。
3、B树的插入：
首先执行查找算法，找出被插结点的父亲结点。
判断被插结点是其父亲结点的左儿子还是右儿子。将被插结点作为叶子结点插入。
若二叉树为空。则首先单独生成根结点。
注意：新插入的结点总是叶子结点，所以算法复杂度是O(h)。
（1）.如果删除的结点没有孩子，则删除后算法结束；
（2）.如果删除的结点只有一个孩子，则删除后该孩子取代被删除结点的位置；
（3）.如果删除的结点有两个孩子，则选择该结点的后继结点（该结点右孩子为根的树中的左子树中的值最小的点）或者前驱节点（该结点左孩子为根的树中的右子树中值最大的点）作为新的根，同时在该后继结点或者前驱节点开始，执行前两种删除算法，删除算法结束。

5.B+树：

一棵m阶的B+树满足下列条件：
（1）每个结点最多m个孩子。
（2）除根结点和叶子结点外，其它每个结点至少有m/2(取上限)个孩子。
（3）根结点至少有两个孩子。
（4）所有的叶子结点在同一层，且包含了所有关键字信息。
（5）有k个孩子的分支结点包含k个关键字。

6.哈夫曼树：

带权路径长度最短的树，权值较大的结点离根较近。

6.散列表：

解决冲突方法：
1.开放定址法 – 探测方式：线性探测、二次探测。
2.分离链接法 – 利用链表的方式。

7.树，森林转化为二叉树

将树转化成二叉树：右子树一定为空
1.加线：在兄弟之间加一连线
2.抹线：对每个结点，除了其左孩子外，去除其与其余孩子之间的关系
3.旋转：以树的根结点为轴心，将整树顺时针转45°
森林转换成二叉树：
1.将各棵树分别转换成二叉树
2.将每棵树的根结点用线相连
3.以第一棵树根结点为二叉树的根

三.疑难问题及解决方案

1.一开始接触二叉平衡树时，对它的构建成一棵树过程比较不理解，在老师讲解后，通过练习现在比较熟练了。

（1）LL情况
设置根节点root的左子节点为新的根节点newroot；
将newroot节点的右子树作为root节点的左子树，将root节点作为newroot的右子树，即降低“左子树”高度，提升“右子树”高度，使得新的左右子树高度趋于平衡。
(2)RR情况
设置根节点root的右子节点为新的根节点newroot；
将newroot节点的左子树作为root节点的右子树，将root节点作为newroot的左子树，即降低“右子树”高度，提升“左子树”高度，使得新的左右子树高度趋于平衡。
(3)LR情况
需要首先对左子树进行左旋操作，调整二叉树为LL情况，再对二叉树执行右旋操作。
(4)RL情况
需要首先对右子树进行右旋操作，调整二叉树为RR情况，再对二叉树执行左旋操作。

2.6-4 jmu-ds-表达式树 (25分)

void InitExpTree(BTree &T,string str)
{
    stack<BTree> num;
    stack<char> ch;
    int i=0;
    ch.push('#');
    while(str[i])
    {
        if(!In(str[i]))
        {
            T=new BTNode;
            T->data=str[i];
            i++;
            T->lchild=T->rchild=NULL;
            num.push(T);
        }
        else
        {
            if(Precede(ch.top(),str[i])=='<')
            {
                ch.push(str[i]);
                i++;
            }
            else if(Precede(ch.top(),str[i])=='=')
            {
                ch.pop();
                i++;
            }
            else
            {
                T=new BTNode;
                T->data=ch.top();
                T->rchild=num.top();
                num.pop();
                T->lchild=num.top();
                num.pop();
                num.push(T);
                ch.pop();
            }
        }
    }
    while(ch.top()!='#')
    {
        T=new BTNode;
        T->data=ch.top();
        T->rchild=num.top();
        num.pop();
        T->lchild=num.top();
        num.pop();
        num.push(T);
        ch.pop();
    }
    T=num.top();
}
double EvaluateExTree(BTree T)
{
    double sum=0,a,b;
    if(!T->lchild&&!T->rchild)
    {
        return T->data-'0';
    }
    a=EvaluateExTree(T->lchild);
    b=EvaluateExTree(T->rchild);
    switch(T->data)
    {
        case'+':
        return a+b;
        case'-':
        return a-b;
        case'*':
        return a*b;
        case'/':
        if(b==0)
        {
            cout<<"divide 0 error!";
            exit(0);
        }
        return a/b;
    }
}

本题一开始并没有太好的思路，在老师的讲解以及百度查询后解了出来