bzoj4144 [AMPPZ2014]Petrol
Description
给定一个 \(n\) 个点、 \(m\) 条边的带权无向图,其中有 \(s\) 个点是加油站。
每辆车都有一个油量上限 \(b\) ,即每次行走距离不能超过 \(b\) ,但在加油站可以补满。
\(q\) 次询问,每次给出 \(x,y,b\) ,表示出发点是 \(x\) ,终点是 \(y\) ,油量上限为 \(b\) ,且保证 \(x\) 点和 \(y\) 点都是加油站,请回答能否从 \(x\) 走到 \(y\) 。
Input
第一行包含三个正整数 \(n,s,m(2\le s\le n\le 200000,1\le m\le 200000)\) ,表示点数、加油站数和边数。
第二行包含 \(s\) 个互不相同的正整数 $c[1],c[2],\cdots c[s] (1\le c[i]\le n) $ ,表示每个加油站。
接下来 \(m\) 行,每行三个正整数 \(u[i],v[i],d[i](1\le u[i],v[i]\le n,u[i]\ne v[i],1\le d[i]\le 10000)\) ,表示 \(u[i]\) 和 \(v[i]\) 之间有一条长度为 \(d[i]\) 的双向边。
接下来一行包含一个正整数 \(q(1\le q\le 200000)\) ,表示询问数。
接下来 \(q\) 行,每行包含三个正整数 \(x[i],y[i],b[i](1\le x[i],y[i]\le n,x[i]\ne y[i],1<\le b[i]\le 2\times 10^9)\) ,表示一个询问。
Output
输出 \(q\) 行。第 \(i\) 行输出第i个询问的答案,如果可行,则输出 \(\mathrm{TAK}\) ,否则输出 \(\mathrm{NIE}\) 。
Sample
Sample Input
6 4 5
1 5 2 6
1 3 1
2 3 2
3 4 3
4 5 5
6 4 5
4
1 2 4
2 6 9
1 5 9
6 5 8
Sample Output
TAK
TAK
TAK
NIE
Solution
真是一道结论诡好题。
大家肯定知道,不是加油站的点是废点。那加油站点该怎么重新建图呢?
来看一个图。红点表示加油站,黑点是废点。
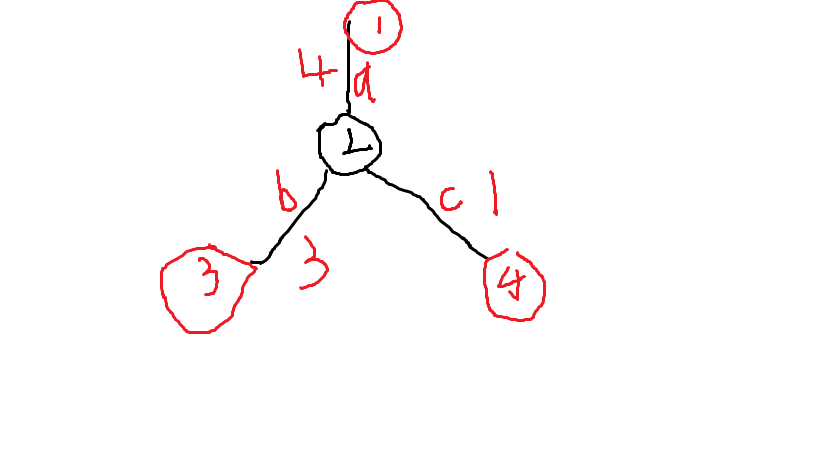
从 \(1\) 到 \(3\) 走简单路径会至少需要 \(7\) 的油量,而从 \(1\) 到 \(4\) 再到 \(3\) 则只需要准备 \(5\) 的油量就可以了。这是因为 $$c<a 且 c<b $$ 所以 $$c+b<a+b 且c+a<b+a$$ 于是我们就得到了结论
- 从当前节点到最近的加油站再到其它的加油站不会更差
那么就可以多源最短路,最小生成树判断连通性就可以了。
具体细节见代码。
#include<bits/stdc++.h>
using namespace std;
#define N 400011
#define rep(i, a, b) for (int i = a; i <= b; i++)
inline int read() {
int x = 0, flag = 1; char ch = getchar(); while (!isdigit(ch)) { if (!(ch ^ '-')) flag = -1; ch = getchar(); }
while (isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar(); return x * flag;
}
int n, s, m, C[N], head[N], tot = 1, cnt, dis[N], near[N], fa[N];
int find(int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }
queue<int> q;
bool inq[N], ans[N];
struct edge { int v, w, next; }e[N];
inline void add(int u, int v, int w) { e[++tot].v = v, e[tot].w = w, e[tot].next = head[u], head[u] = tot; }
struct edgeData {
int u, v, w;
edgeData(int _u = 0, int _v = 0, int _w = 0):u(_u), v(_v), w(_w) {}
bool operator < (const edgeData& b) const { return w < b.w; }
}edt[N];
struct query {
int id, S, T, d;
bool operator < (const query& b) const { return d < b.d; }
}qu[N];
void spfa() {
rep(i, 1, n) dis[i] = 0x7fffffff;
rep(i, 1, s) q.push(C[i]), inq[C[i]] = 1, dis[C[i]] = 0, near[C[i]] = C[i];
while (!q.empty()) {
int u = q.front(); q.pop(), inq[u] = 0;
for (int i = head[u], v; i; i = e[i].next) if (dis[v = e[i].v] > dis[u] + e[i].w) {
dis[v] = dis[u] + e[i].w, near[v] = near[u];
if (!inq[v]) q.push(v), inq[v] = 1;
}
}
rep(u, 1, n) for (int i = head[u], v; i; i = e[i].next) if (near[u] ^ near[v = e[i].v])
edt[++cnt] = edgeData(near[u], near[v], dis[u] + dis[v] + e[i].w);
sort(edt + 1, edt + 1 + cnt);
}
int main() {
n = read(), s = read(), m = read();
rep(i, 1, n) fa[i] = i;
rep(i, 1, s) C[i] = read();
rep(i, 1, m) { int u = read(), v = read(), w = read(); add(u, v, w), add(v, u, w); }
spfa();
int q = read();
rep(i, 1, q) qu[i].S = read(), qu[i].T = read(), qu[i].d = read(), qu[i].id = i;
sort(qu + 1, qu + 1 + q);
int pos = 1;
rep(i, 1, q) {
while (pos <= cnt && edt[pos].w <= qu[i].d) {
int x = find(edt[pos].u), y = find(edt[pos].v);
if (x ^ y) fa[x] = y;
pos++;
}
ans[qu[i].id] = (find(qu[i].S) == find(qu[i].T));
}
rep(i, 1, q) puts(ans[i] ? "TAK" : "NIE");
return 0;
}



