科普向：全连接神经网络

## 科普向：全连接神经网络

“We can only see a short distance ahead, but we can see plenty there that needs to be done.”
                                                                                 —————Turing

在CNN、RNN（LSTM/GRU）、Transformer等各种神经网络实现弱人工智能的时代，神经网络似乎成为了一种神奇的黑盒，神秘而强大。
而上述神经网络都是基于全连接神经网络出发的，最基础的原理都是由反向传播而来。作为深度神经网络（DNN, Deep Neural Networks）的开始，从感知机（Perceptron）到全连接神经网络（Fully Connected Neural Network）再至上如经典神经网络模型，神经网络的前世今生美妙精彩，下面让我们了解全连接神经网络吧。

                                                    

 

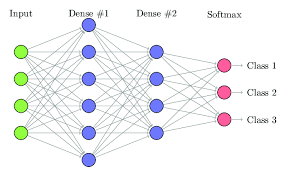
如上图全连接神经网络可简化为左边输入，中间计算，右边输出。（其中Dense便是经典的全连接层）

 

Dense1 = Input * W1 + b1
Dense2 = Dense * W2 + b2
Output = F（Dense2 * W3 + b3）

F一般为激活函数，如上图便是多分类所使用的softmax
（激活函数可视为能将数值按大小缩放至0-1的概率表示器）

 

 

如我们想要做一个数字分类器 （此处的数字是抽象意义的数字，一般实际情况为图片、文本、语音等真实数据）0-9为1 ， 10-99为2，100-999为3
举例：Input = [5，20，521] , 与之对应我们希望Output = [1, 2, 3]。
但我们只有 已知数据集 I = [1,10,100] 和 O = [1, 2, 3]，我们能否通过全连接神经网络训练得到期望的模型可以解决Input的正确Ouput，答案是肯定的。

网络中的参数W1、b1、W2、b2便是我们所需要“训练”的，而训练原理便是根据反向传播（BP,Error Back Propagation）得到。
具体为可先随机初始化参数，将我们的已知数据集I 得到 输出 O_I , 再根据BP梯度下降等方法多次迭代修改参数W1、b1、W2、b2，最终完成我们的全连接神经网络。在一定数据量下可以通过这种简单粗暴的方式训练出很棒的全连接神经网络。

总结：
**优点**：不要求输入尺寸为固定尺寸、综合所有信息
               对于大多数神经网络层要求输入尺寸固定，但对于Dense全连接层或整个全连接神经网络不要求输入尺寸，只要全部相连即可，这样保证了全部信息的整合。
**缺点**：参数量大、空间结构的表达性差（平铺降维信息）
               单一Dense全连接层的参数量会递乘至下一层导致参数量过大，因为全连接的处理方式相当于特征线性组合、截断，对于诸如三维信息经过全连接层只会表示成二维信息。