CNN经典网络——Resnet以及Keras实现
由于笔者水平有限,如有错,欢迎指正。
来源
深度残差网络(Deep residual network, ResNet)的提出是CNN图像史上的一件里程碑事件,何凯明团队提出的该网络在ILSVRC和COCO 2015上获得了5项第一。那么为什么ResNet会有如此优异的表现呢?
我们的一般印象当中,深度学习愈是深(复杂,参数多)愈是有着更强的表达能力。凭着这一基本准则,CNN分类网络自Alexnet的7层发展到了VGG的16乃至19层,后来更有了Googlenet的22层。可后来我们发现深度CNN网络达到一定深度后再一味地增加层数并不能带来进一步地分类性能提高,反而会招致网络收敛变得更慢,分类准确率也变得更差。排除数据集过小带来的模型过拟合等问题后,我们发现过深的网络仍然还会使分类准确度下降(相对于较浅些的网络而言)。
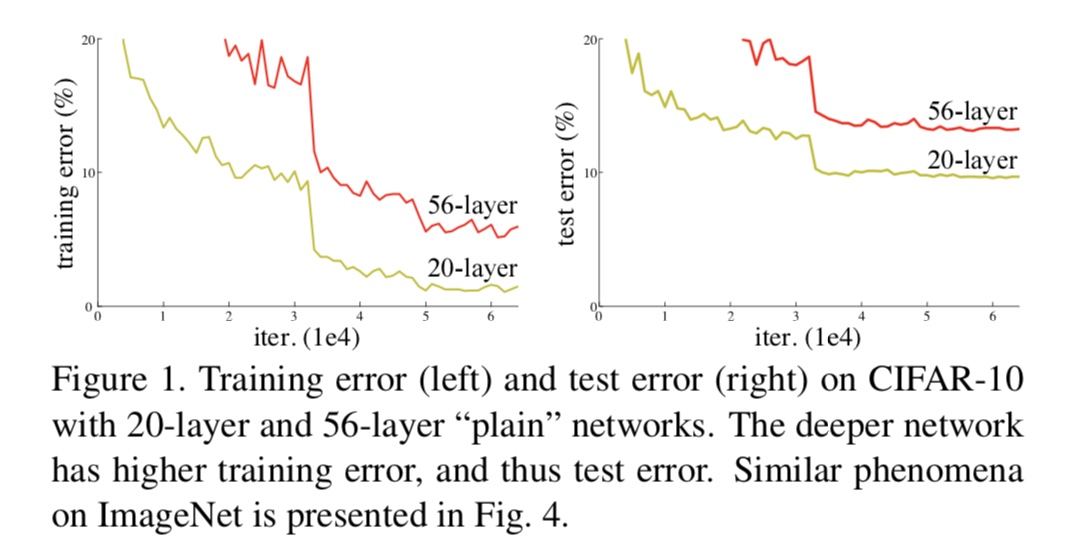
正如上图及其注解所示,56层的网络比20层还要差很多。在此基础上,何凯明博士提出了残差学习来解决退化问题。
残差学习(Residual learning)
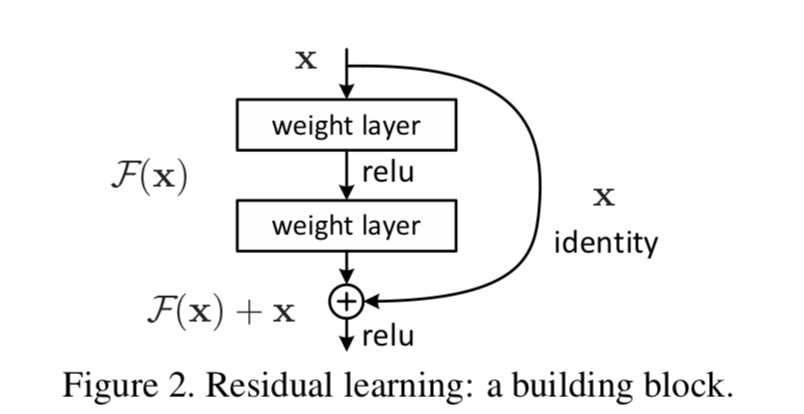
上图是一个残差学习单元,把一个输入x和其堆叠了2次后的输出F(x)的进行元素级和作为总的输出。因此它没有增加网络的运算复杂度,把原来需要学习逼近的未知函数H(x)恒等映射(Identity mapping),变成了逼近F(x)=H(x)-x的一个函数。这两种表达的效果相同,但是优化的难度却并不相同,作者假设F(x)的优化会比H(x)简单的多。
在论文中,作者设计了实验,两个参数量、计算量相同的网络,仅仅是在其一插入了shortcut,就达到了优化的目的,得到了更好的效果。
ResNet in Keras
- 使用identity_block这个函数来搭建Resnet34,使用bottleneck这个函数来搭建Resnet50。 右图为bottleneck
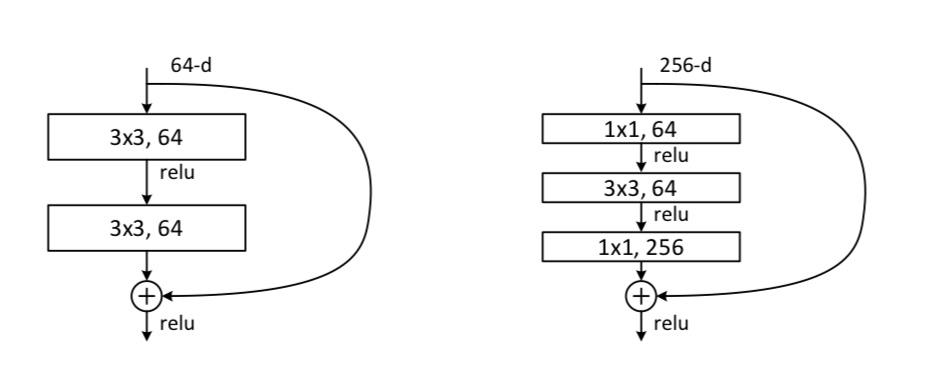
- 每个卷积层后都使用BatchNormalization,来防止模型过拟合,并且使输出满足高斯分布。
identity_block(ResNet34) :
def identity_block(X, f, filters, stage, block):
# defining name basis
conv_name_base = "res" + str(stage) + block + "_branch"
bn_name_base = "bn" + str(stage) + block + "_branch"
# Retrieve Filters
F1, F2, F3 = filters
# Save the input value. You'll need this later to add back to the main path.
X_shortcut = X
# First component of main path
X = Conv2D(filters=F1, kernel_size=(1, 1), strides=(1, 1), padding="valid",
name=conv_name_base+"2a", kernel_initializer=glorot_uniform(seed=0))(X)
#valid mean no padding / glorot_uniform equal to Xaiver initialization - Steve
X = BatchNormalization(axis=3, name=bn_name_base + "2a")(X)
X = Activation("relu")(X)
### START CODE HERE ###
# Second component of main path (≈3 lines)
X = Conv2D(filters=F2, kernel_size=(f, f), strides=(1, 1), padding="same",
name=conv_name_base+"2b", kernel_initializer=glorot_uniform(seed=0))(X)
X = BatchNormalization(axis=3, name=bn_name_base+"2b")(X)
X = Activation("relu")(X)
# Third component of main path (≈2 lines)
# Final step: Add shortcut value to main path, and pass it through a RELU activation (≈2 lines)
X = Conv2D(filters=F3, kernel_size=(1, 1), strides=(1, 1), padding="valid",
name=conv_name_base+"2c", kernel_initializer=glorot_uniform(seed=0))(X)
X = BatchNormalization(axis=3, name=bn_name_base+"2c")(X)
X = Add()([X, X_shortcut])
X = Activation("relu")(X)
### END CODE HERE ###
return X
bottleneck_Block(ResNet50):
def bottleneck_Block(X, f, filters, stage, block, s = 2):
# defining name basis
conv_name_base = 'res' + str(stage) + block + '_branch'
bn_name_base = 'bn' + str(stage) + block + '_branch'
# Retrieve Filters
F1, F2, F3 = filters
# Save the input value
X_shortcut = X
##### MAIN PATH #####
# First component of main path
X = Conv2D(F1, (1, 1), strides = (s,s), name = conv_name_base + '2a', padding='valid', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2a')(X)
X = Activation('relu')(X)
### START CODE HERE ###
# Second component of main path (≈3 lines)
X = Conv2D(F2, (f, f), strides = (1, 1), name = conv_name_base + '2b',padding='same', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2b')(X)
X = Activation('relu')(X)
# Third component of main path (≈2 lines)
X = Conv2D(F3, (1, 1), strides = (1, 1), name = conv_name_base + '2c',padding='valid', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2c')(X)
##### SHORTCUT PATH #### (≈2 lines)
X_shortcut = Conv2D(F3, (1, 1), strides = (s, s), name = conv_name_base + '1',padding='valid', kernel_initializer = glorot_uniform(seed=0))(X_shortcut)
X_shortcut = BatchNormalization(axis = 3, name = bn_name_base + '1')(X_shortcut)
# Final step: Add shortcut value to main path, and pass it through a RELU activation (≈2 lines)
X = layers.add([X, X_shortcut])
X = Activation('relu')(X)
### END CODE HERE ###
return X
ResNet50 :
def ResNet50(input_shape = (64, 64, 3), classes = 6):
# Define the input as a tensor with shape input_shape
X_input = Input(input_shape)
# Zero-Padding
X = ZeroPadding2D((3, 3))(X_input)
# Stage 1
X = Conv2D(filters=64, kernel_size=(7, 7), strides=(2, 2), name="conv",
kernel_initializer=glorot_uniform(seed=0))(X)
X = BatchNormalization(axis=3, name="bn_conv1")(X)
X = Activation("relu")(X)
X = MaxPooling2D(pool_size=(3, 3), strides=(2, 2))(X)
# Stage 2
X = convolutional_block(X, f=3, filters=[64, 64, 256], stage=2, block="a", s=1)
X = identity_block(X, f=3, filters=[64, 64, 256], stage=2, block="b")
X = identity_block(X, f=3, filters=[64, 64, 256], stage=2, block="c")
### START CODE HERE ###
# Stage 3 (≈4 lines)
# The convolutional block uses three set of filters of size [128,128,512], "f" is 3, "s" is 2 and the block is "a".
# The 3 identity blocks use three set of filters of size [128,128,512], "f" is 3 and the blocks are "b", "c" and "d".
X = convolutional_block(X, f=3, filters=[128, 128, 512], stage=3, block="a", s=1)
X = identity_block(X, f=3, filters=[128, 128, 512], stage=3, block="b")
X = identity_block(X, f=3, filters=[128, 128, 512], stage=3, block="c")
X = identity_block(X, f=3, filters=[128, 128, 512], stage=3, block="d")
# Stage 4 (≈6 lines)
# The convolutional block uses three set of filters of size [256, 256, 1024], "f" is 3, "s" is 2 and the block is "a".
# The 5 identity blocks use three set of filters of size [256, 256, 1024], "f" is 3 and the blocks are "b", "c", "d", "e" and "f".
X = convolutional_block(X, f=3, filters=[256, 256, 1024], stage=4, block="a", s=2)
X = identity_block(X, f=3, filters=[256, 256, 1024], stage=4, block="b")
X = identity_block(X, f=3, filters=[256, 256, 1024], stage=4, block="c")
X = identity_block(X, f=3, filters=[256, 256, 1024], stage=4, block="d")
X = identity_block(X, f=3, filters=[256, 256, 1024], stage=4, block="e")
X = identity_block(X, f=3, filters=[256, 256, 1024], stage=4, block="f")
# Stage 5 (≈3 lines)
# The convolutional block uses three set of filters of size [512, 512, 2048], "f" is 3, "s" is 2 and the block is "a".
# The 2 identity blocks use three set of filters of size [256, 256, 2048], "f" is 3 and the blocks are "b" and "c".
X = convolutional_block(X, f=3, filters=[512, 512, 2048], stage=5, block="a", s=2)
X = identity_block(X, f=3, filters=[512, 512, 2048], stage=5, block="b")
X = identity_block(X, f=3, filters=[512, 512, 2048], stage=5, block="c")
# filters should be [256, 256, 2048], but it fail to be graded. Use [512, 512, 2048] to pass the grading
# AVGPOOL (≈1 line). Use "X = AveragePooling2D(...)(X)"
# The 2D Average Pooling uses a window of shape (2,2) and its name is "avg_pool".
X = AveragePooling2D(pool_size=(2, 2), padding="same")(X)
### END CODE HERE ###
# output layer
X = Flatten()(X)
X = Dense(classes, activation="softmax", name="fc"+str(classes), kernel_initializer=glorot_uniform(seed=0))(X)
# Create model
model = Model(inputs=X_input, outputs=X, name="ResNet50")
return model
参考资料
https://www.jianshu.com/p/93990a641066
https://www.cnblogs.com/long5683/p/12957042.html
吴恩达ResNet作业: https://blog.csdn.net/Solo95/article/details/85177557



