机器学习——贝叶斯方法

0.什么是贝叶斯？

贝叶斯公式是由一位数学家——托马斯·贝叶斯提出的，也称为贝叶斯法则，他在许许多多的领域都有所应用，我们也在许多数学课程中学习过他。

这就是说，当你不能准确知悉一个事物的本质时，你可以依靠与事物特定本质相关的事件出现的多少去判断其本质属性的概率。用数学语言表达就是：支持某项属性的事件发生得愈多，则该属性成立的可能性就愈大。

它告诉我们当我们要预测一个事物，我们需要的是首先根据已有的经验和知识推断一个先验概率，然后在新证据不断积累的情况下调整这个概率。整个通过积累证据来得到一个事件发生概率的过程我们称为贝叶斯分析。

由于笔者水平有限，在此对贝叶斯的深度理解及其推导不做讨论，http://mindhacks.cn/2008/09/21/the-magical-bayesian-method/ 刘未鹏大神的这篇文章由浅入深的讲述了贝叶斯的方法，非常值得阅读。

1.贝叶斯决策论

先验概率：通俗来说，对于某一个概率事件，我们都会有基于自己已有的知识，对于这个概率事件会分别以什么概率出现各种结果会有一个预先的估计，而这个估计并未考虑到任何相关因素。

后验概率是指：当与事件相关的一些证据或背景也被考虑进来时的条件概率。

总的来说，先验概率基于已有知识对随机事件进行概率预估，但不考虑任何相关因素(P(y))。后验概率基于已有知识对随机事件进行概率预估，并考虑相关因素(P(y|x))。

$P(y|x)=\frac{P(y)P(x|y)}{P(x)}=\frac{P(x,y)}{P(x)}$

X是依赖特征向量（大小为n）例： X=（下雨，刮风，气温高）

Y是类变量例： y = 已知天气情况X，是否能出门玩

P(y|x)：在x的条件下，随机事件出现c情况的概率。（后验概率）
P(y)：（不考虑相关因素）随机事件出现c情况的概率。（先验概率）
P(x|y)：在已知事件出现c情况的条件下，条件x出现的概率。（c的后验概率）
P(x)：x出现的概率。（先验概率）

2. 朴素贝叶斯分类器

2.0 前提

朴素贝叶斯算法的朴素之处在于：假设所有用于分类的特征都是相互独立的。

例如温度热不热跟湿度没有任何关系，天气是否下雨也不影响是否刮风。因此，这就是假设特征相互独立。
每个特征都有相同的权重（或者是重要性）
只能应用在离散数据上

2.1 朴素贝叶斯分类器表达式

由数学推导得到分类模型：

$$h_{nb}(x)=argmax_{c\in y} P(c)\Pi_{i=1}^dP(x_i|c)$$

它的值就是贝叶斯分类器对于给定x的因素下，最可能出现的情况c。y是c的取值集合

3. 半朴素贝叶斯分类器

3.0 起始

由于朴素贝叶斯有着 “特征都是相互独立” 的限制，但这个假设几乎不存在。因为往往属性之间都有所关联。于是，人们进行改进之后产生了半朴素贝叶斯分类器（semi-naive Bayes classifiers）。

3.1 独依赖估计（One-Dependent Estimator，简称ODE）

独依赖估计半朴素贝叶斯分类器最常用的一种策略。独依赖是假设每个属性在类别之外最多依赖一个其他属性，下图公式中的paj为属性xi所依赖的属性，称为xi的父属性。

于是，问题的关键变成了如何确定每个属性的父属性。不同的做法产生了不同的独依赖分类器。

SPODE（Super-Parent ODE）这种方法假定所有的属性都依赖于共同的一个父属性。
TAN（Tree Augmented naive Bayes）每个属性依赖的另外的属性由最大带权生成树来确定。
AODE（Averaged ODE）是一种集成学习的方法，尝试将每个属性作为超父来构建SPODE，与随机森林的方法有所相似。

4. 贝叶斯网

4.0 起始

贝叶斯网络(Bayesian network)，又称信念网络(Belief Network)，或有向无环图模型(directed acyclic graphical model)，是一种概率图模型，比朴素贝叶斯更复杂，但由于贝叶斯网络

4.1 有向无环图（DAG）

下图中这样一个简单的网络对应着全概率公式，P(a,b,c) = P(a)P(b)P(c|a,b)

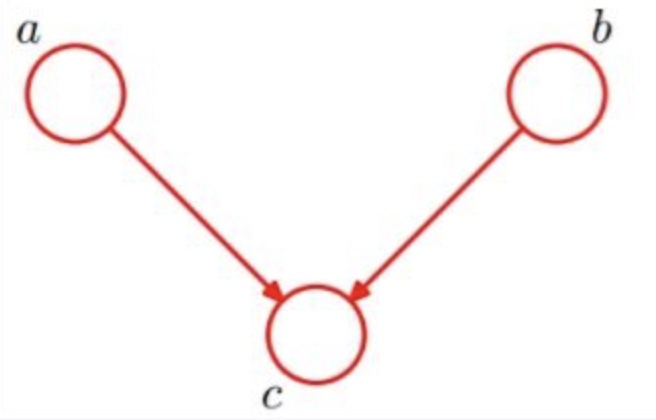
4.2 定义

一个贝叶斯网络定义包括一个有向无环图（DAG）和一个条件概率表集合。

下图为一个Student模型对应的概率图，作为参考

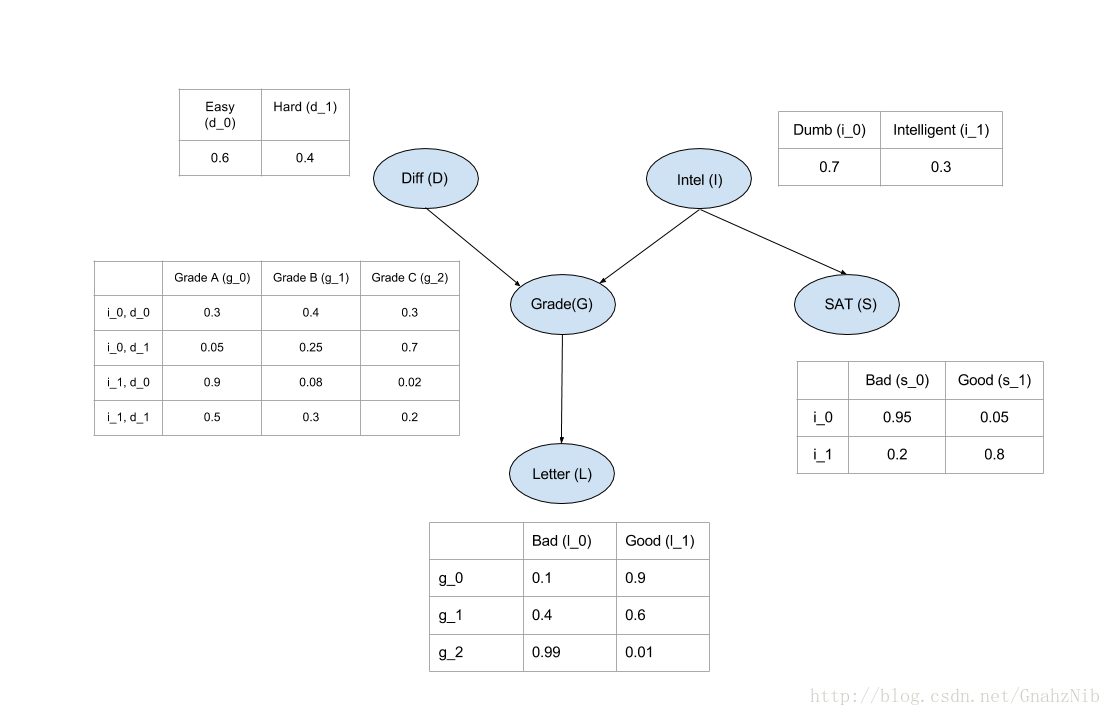
5. EM算法

5.0 定义

EM的计算方法中每一次迭代都分两步，其中一个为期望步（E步），另一个为极大步（M步），所以算法被称为EM算法（Expectation Maximization Algorithm）。

由于笔者理解EM略有困难，还需要学习，在这里参考知乎@文兄的解释

借用我之前看到的一个例子来讲一下EM算法吧。

现在一个班里有50个男生，50个女生，且男生站左，女生站右。我们假定男生的身高服从正态分布 $N(\mu_1,\sigma_1^2)$ ，女生的身高则服从另一个正态分布： $N(\mu_2,\sigma_2^2)$ 。这时候我们可以用极大似然法（MLE），分别通过这50个男生和50个女生的样本来估计这两个正态分布的参数。

但现在我们让情况复杂一点，就是这50个男生和50个女生混在一起了。我们拥有100个人的身高数据，却不知道这100个人每一个是男生还是女生。

这时候情况就有点尴尬，因为通常来说，我们只有知道了精确的男女身高的正态分布参数我们才能知道每一个人更有可能是男生还是女生。但从另一方面去考量，我们只有知道了每个人是男生还是女生才能尽可能准确地估计男女各自身高的正态分布的参数。

这个时候有人就想到我们必须从某一点开始，并用迭代的办法去解决这个问题：我们先设定男生身高和女生身高分布的几个参数（初始值），然后根据这些参数去判断每一个样本（人）是男生还是女生，之后根据标注后的样本再反过来重新估计参数。之后再多次重复这个过程，直至稳定。这个算法也就是EM算法。