最长公共子序列(LCS)

　　以前一直不懂LCS问题，然而找工作被LCS折磨的，与那个公司无缘了。

　　最长公共子序列问题是一道经典的动态规划问题，最长公共子序列问题也有最优子结构。

即：Xi<x1, x2,..., xi>即X序列的前i个字符(1<=i<=m)，Yj<y1, y2,..., yj)即Y序列的前j个序列(1<=j<=n);假设Z<z1,z2,...,Zk>属于LCS(X,Y);

若：xm==yn(最后一个字符相同),则不难用反证法证明：该字符必是X与Y的任一最长公共子序列Z（设长度为k）的最后一个字符，即有zk = xm = yn 且显然有Zk-1∈LCS(Xm-1 , Yn-1)即Z的前缀Zk-1是Xm-1与Yn-1的最长公共子序列。此时，问题化归成求Xm-1与Yn-1的LCS（LCS(X , Y)的长度等于LCS(Xm-1 , Yn-1)的长度加1）。

若：xm≠yn，则亦不难用反证法证明：要么Z∈LCS(Xm-1, Y)，要么Z∈LCS(X , Yn-1)。由于zk≠xm与zk≠yn其中至少有一个必成立，若zk≠xm则有Z∈LCS(Xm-1 , Y)，类似的，若zk≠yn 则有Z∈LCS(X , Yn-1)。此时，问题化归成求Xm-1与Y的LCS及X与Yn-1的LCS。LCS(X , Y)的长度为：max{LCS(Xm-1 , Y)的长度, LCS(X , Yn-1)的长度}。

由于上述当xm≠yn的情况中，求LCS(Xm-1 , Y)的长度与LCS(X , Yn-1)的长度，这两个问题不是相互独立的：两者都需要求LCS(Xm-1，Yn-1)的长度。另外两个序列的LCS中包含了两个序列的前缀的LCS，故问题具有最优子结构性质考虑用动态规划法。

    也就是说，解决这个LCS问题，你要求三个方面的东西：1、LCS（Xm-1，Yn-1）+1；2、LCS（Xm-1，Y），LCS（X，Yn-1）；3、max{LCS（Xm-1，Y），LCS（X，Yn-1）}。

由上述可以得出递归公式：

 

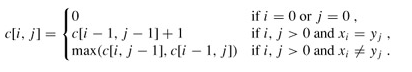
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
enum decreaseDir {kInit = 0, kLeft, kUp, kLeftUp};
string ret;
void LCS_Print(vector<vector<int> > &dir, const char *str1, const char *str2, int row, int col)
{
    if(str1 == NULL || str2 == NULL)
        return;
    int len1 = strlen(str1);
    int len2 = strlen(str2);
    if(len1 == 0 || len2 == 0 || !(row < len1 && col < len2 ))
        return;
    if(dir[row][col] == kLeftUp)
    {
        if(row > 0 && col > 0)
            LCS_Print(dir, str1, str2, row - 1, col -1);
        ret.push_back(str1[row]);
    }
    else if(dir[row][col] == kUp)
    {
        if(row > 0)
            LCS_Print(dir, str1, str2, row - 1, col);
    }
    else if(dir[row][col] == kLeft)
    {
        if(col > 0)
            LCS_Print(dir, str1, str2, row, col -1);
    }
}
int LCS(const char *str1, const char *str2)
{
    if(!str1 || !str2)
        return 0;
    int len1 = strlen(str1);
    int len2 = strlen(str2);
    if(!len1 || !len2)
        return 0;
    int i, j;
    vector<vector<int> > dp(len1, vector<int>(len2, 0));
    vector<vector<int> > dir(len1, vector<int>(len2, 0));
    for(int i = 0; i < len1; i++)
    {
        for(int j = 0; j < len2; j++)
        {
            if(i == 0 || j == 0)
            {
                if(str1[i] == str2[j])
                {
                    dp[i][j] = 1;
                    dir[i][j] = kLeftUp;
                }
                else
                {
                    if(i > 0)
                    {
                        dp[i][j] = dp[i-1][j];
                        dir[i][j] = kUp;
                    }
                    if(j > 0)
                    {
                        dp[i][j] = dp[i][j-1];
                        dir[i][j] = kLeft;
                    }
                }
            }
            else if(str1[i] == str2[j])
            {
                dp[i][j] = dp[i-1][j-1] + 1;
                dir[i][j] = kLeftUp;
            }
            else if(dp[i-1][j] > dp[i][j-1])
            {
                dp[i][j] = dp[i-1][j];
                dir[i][j] = kUp;
            }
            else
            {
                dp[i][j] = dp[i][j-1];
                dir[i][j] = kLeft;
            }
        }
    }
    LCS_Print(dir, str1, str2, len1 - 1, len2 - 1);
    return dp[len1-1][len2-1];
}
int main()
{
    const char *str1 = "abcde";
    const char *str2 = "acde";
    ret.clear();
    int longest = LCS(str1, str2);
    cout << "longest = " << longest << endl;
    cout << "ret = " << ret << endl;
    return 0;
}