超参数调试、Batch正则化和程序框架
调试处理
关于训练深度最难的事情 之一是你要处理参数的数量,从学习速率α到momentum(术语)β。
如果使用momentum或Adam优化算法的参数,可能你还得选择层数,选择不同层中隐藏单元的数量。也许你还想使用学习率衰退,所以你使用的不是单一的学习速率α。你可能还需要选择Mini-batch的大小。结果证实一些超参数比其它的更为重要
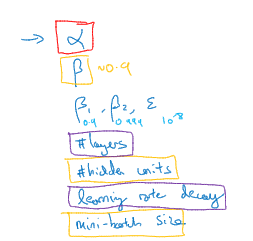
现在如果你尝试调整一些超参数,该如何选择调试值
在早一代的机器学习算法中,如果你有两个超参数。这里称之为超参一,超参二。常见的做法是在网格中取样点。像这样然后系统 的研究这些数值。网格可以是5*5,也可多或少。当参数的数量相对较少时,这个方法很实用、
在深度学习领域,我们的做法是,随机选择点,我们可以选择同等数量的点,接着用这些随机取的点试验超参数的效果。之所以这么做是因为对于你要解决的问题而言,你很难提前知道哪个超参数最重要。

为超参选择合适的范围
假设你要选择隐藏单元的数量n[l],对于给定层1而言。假设你选择的取值范围是从50到100中某点,这种情况下,看到这条从50-100的数轴,你可以随机在其上取点

这是一个搜获特定超参的很直观的方式,或者如果你要选取神经网络的层数你也许会选择层数为2到4中的某个值。接着顺着2,3,4随机均匀取样才比较合理。你还可以应用网格搜索,你会觉得2,3,4这三个数值是合理的。
看这个例子,假设你在搜索超参α学习速率,你怀疑其值最小是0.0001或最大是1。画一条从0,0001到1的数轴,沿其随机均匀取值,那90%的数值将会落在0.1到1之间,结果就是在0.1到1之间应用了90%的资源,而0.0001到0.1之间只有10%的搜索资源,不太合理
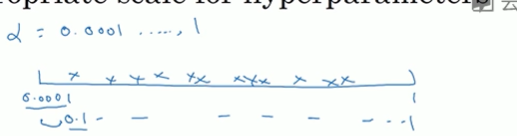
反而用对数标尺搜索超参的方式会更合理,这里不使用线性轴,在对数轴上均匀随机取点

这样在0.0001到0.001之间就会有更多的搜索资源可用
我们在python写代码的时候可以使用
然后α随机取值α=10^r,你要做的就是在[a,b]区间随机均匀地给r取值,这个例子中是r属于[-4,0]。然后可以设置α的值
总结,在对数坐标上取值,取最小值的对数就得到a值,取最大值的对数就得到b值。所以现在你在对数轴上的10^a到10^b区间取值,在a,b间随意均匀的选择r值,将超参设置为10^r。这就是在对数轴上取值的过程

最后,另一个例子就是给β取值,用于计算指数的加权平均值,假设你认为β是0.9到0.999之间的某个值
记住,当计算指数的加权平均值时,取0.9就像在10个值中计算平均值。
我们要探究的是1-β,此值在0.1到0.001区间内
所以你要做的就是在[-3,-1]里随机均匀的给r取值,1-β=10^r,所以β=1-10^r
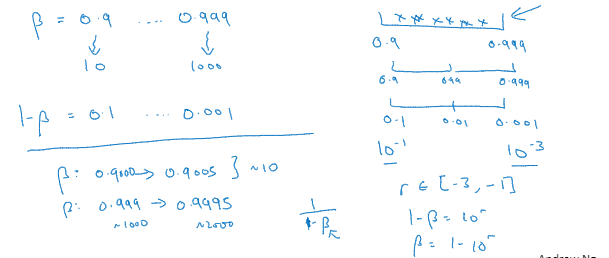
正则化网络的激活函数
Batch归一化会使用你的参数搜索问题变得很容易,使神经网络对超参数的选择更加稳定,超参的范围会更庞大,工作效果也很好,也会使你很容易的训练甚至是深层网络。
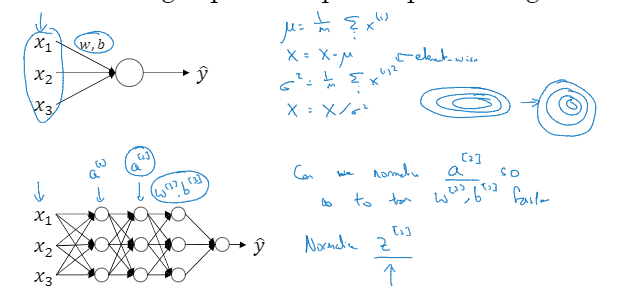
当你训练一个模型,比如logistic回归时,你也许会记得归一化输入特征可加速学习过程,你计算了平均值,从训练集中减去平均值,计算了方差x^(i)的平方和,接着根据方差归一化你的数据集。
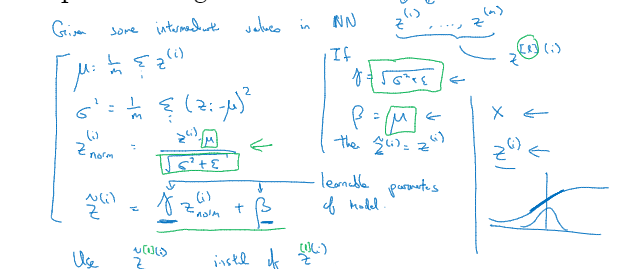
将Batch Norm拟合进神经网络
假设有一这样的神经网络,你可以认为每个单元负责计算两件事,第一,它先计算Z,然后应用其到激活函数中在计算a,每个圆圈代表着两步的计算过程。
Softmax回归
有一种logistic回归的一般形式叫做Softmax回归,能让你在试图识别某一分类时做出预测或者说是多种分类中的一个不只是识别两个分类
假设你不单需要识别猫,而是想要识别猫狗和小鸡。我们把猫叫做类1,狗为类2,小鸡是类3,如果不属于以上任何一类就分到其他。此类称为类0。

用大写C表示你的输入会被分入的类别总个数,这个例子中有4种可能的类别
C=4

这里的y帽将是一个4*1维向量,因为它必须输出四个数字,给你这四种概率。因为它加起来应该等于1,输出的y帽中的四个数字加起来应该等于1。
让你的网络做到这一点的标准模型要用到Softmax层以及输出层来生成输出。
在神经网络的最后一层你将会像往常一样计算各层的线性部分z,L这是最后一层的变量,计算方法是w^[L]乘以上一无尾熊的激活值,再加上最后一层的偏差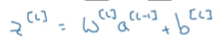
之后你需要应用Softmax激活函数,此激活函数的作用,首先我们要计算一个临时变量,我们把它叫做t,它等于e的z^[L]次方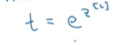
这适用于每个元素。

这个计算过程可以概括为是一个Softmax激活函数
深度学习框架

TensorFlow
损失函数
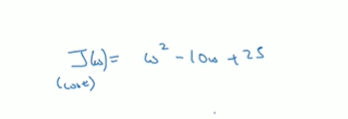
你可以使用TensorFlow自动找到使用损失函数最小的w和b的值
后面是真听不懂了。。。啊!!!



