优化算法
Mini-batch 梯度下降法
优化算法能让你的神经网络运行得更快。
之前我们所了解的向量化能让我们有效地对所有m个例子进行计算，允许 你处理整个训练集，而无需某个明确的公式 ，所以我们要把训练样本放到巨大的矩阵X当中去
一直到第X^(m)个训练样本，y也是如此
所以x的维数是(n_x,m)，y的维数是(1,m),向量化能让我们相对较快地处理所有m个样本，但如果m很大的话，处理速度仍然缓慢。在对整个训练 集执行梯度下降法时，我们必须处理整个训练集，然后才能进行一步梯度下降法，然后需要再重新处理。
为了方便的话，你可以把训练集分割为小一点的子训练 集，这些子集被取名为Mini-batch
假设每一个子集中只有1000个样本，那么你其中的x^(1)到x^(1000)取出来 ，将其称之为第一个子训练集也叫Mini-batch,然后你再取出接下来的1000个样本，从X^(1001)到X^(2000),然后再取1000个样本，以此类推
新符号：x^{1}；Mini-batch数量t组成了X^{t}和Y^{t}，这就是1000个训练样本包含相应的输入输出对、
batch梯度下降法指的是，我们之前学的梯度下降法算法就是同时处理整个训练集，能够同时看到整个batch训练集的样本被处理
mini-batch梯度下降法比batch梯度下降法运行地更快
理解Mini-batch梯度下降法
在使用batch梯度下降法的时候每次迭代你都需要遍历整个训练集，预期每次迭代的成本都会下降，所以如果成本函数J是迭代次数的一个函数，它应该会随着每次迭代而减少，如果J在某次迭代中增加了那肯定出了问题
使用mini-batch梯度下降法，如果你作出成本函数在整个过程中的图，则并不是每次迭代都是下降的，特别是在每次迭代中，你要处理的是X^{t} Y^{t}。如果要作出成本函数J^{t}的图，而J^{t}只和X^{t} Y^{t}有关，也就是每次迭代下你都在训练不同的样本集，如果你要作出成本函数J的图，你很可能会看到这样的结果
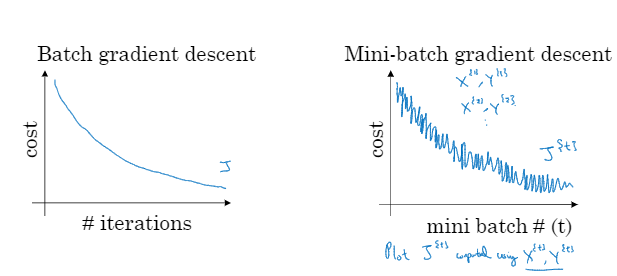
你需要决定的变量之一是mini-batch的大小，m就是训练集的大小。如果mini-batch的大小=m,其实就是batch 梯度下降法。所以把mini-batch大小设为m可以得到batch梯度下降法，另一种情况,假设mini-batch大小为1就有了新的算法，叫做随机梯度下降法，每个样本都是独立的mini-batch
指数加权平均
举个例子说明一下
利用天气的温度
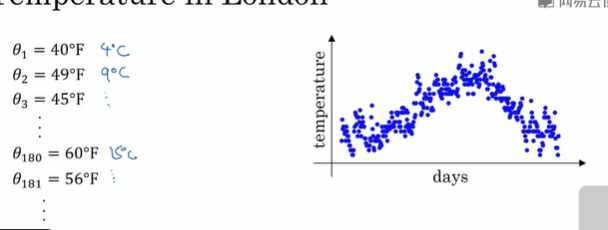
利用数据作图，可以得到以上结果 ，起始日在1月份，中间部分是夏季初，最后是年末，相当于12月末。如果要计算趋势的话，也就是温度的局部平均值，或者说是移动平均值，我们要做的是首先使用V_0=0，每天需要使用0.9的加权数之前的数值加上当日温度的0.1，这就是第一天的温度，第二天又可以嘛 获得一个加权平均数，以此类推，像这样
然后以红线作图，得到移动平均值
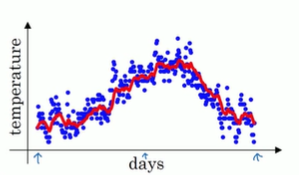
这就是公式，在计算时可视V_t为
假如是把β=0.98，然后代入那个公式，1/(1-β)，大约等于50，所以这就代表的是过去50天的温度
动量梯度下降法
这个动量梯度下降法的运行速度是要快于标准的梯度下降算法，基本的想法就是计算梯度的指数加权平均数并利用该梯度更新欠的权重 。
例如，如果 你要优化成本函数，函数形状如图，红点代表最小值 的位置。假设你从这里开始梯度下降法，如果进行梯度下降法的一次迭代，无论是batch或mini-batch下降法也许会指向这里，现在在椭圆的另一边计算下一步梯度下降，我们要计算很多步，一直到最小值，这种上下波动减慢了梯度下降法的速度，我们就无法使用更大的学习率了。
从另一个角度来看，在纵轴上，你希望学习慢一点，而在横轴上你希望加速学习，你希望快速从左向右移，移向最值，移向红点。
所以使用momentum梯度下降法需要做的是，在每次迭代中确切来说在第t次迭代的过程中，你会计算微分dw、db。我会省略上标括号l，你用现有的mini-batch计算dw、db,如果你用batch梯度下降法，现在在mini-batch就是全部的batch，对于batch梯度下降法的效果是一样的。我们要做的是
，计算到的是dw的移动平均数
，然后重新赋值权重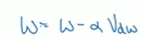
，这样就杺减缓梯度下降的幅度
RMSprop算法
此算法也可以加速梯度下降
回忆之前的例子，如果你执行梯度下降，虽然横轴方向正在推进，但纵轴方向会有大幅度摆动。为了分析这个例子，假设纵轴代表参数b横轴代表参数W，可能有W1，W2或者其他重要的参数。为了便于理解，被称为b和w。
所以你想减缓b方向的学习，即纵轴方向，同时加快，至少不是减缓横轴方向的学习。RMSprop算法可以实现这一点，在第t次迭代中该算法会照常计算当下mini-batch的微分dw db。所以我会保留这个指数加权平均数，我要用到新符号S_dw
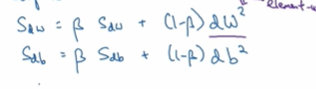
接着RMSprop会这样更新参数值
Adam优化算法
使用Adam算法，首先你要初始化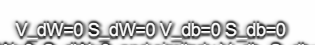
在第t次迭代中你要计算微分 用当前的mini-batch计算dw db ，接下来计算momentum指数加权平均数，然后
接着使用RMSprop进行更新
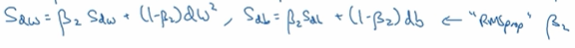
就是用momentun更新了超参数β1，用RMSprop更新了超参数β2，一般使用Adam算法的时候要计算偏差修正
更新W和b，就用V_dw或者修正后的V_dw，但现在我们加入了RMSprop的部分，所以我们还要除以修正后的S_dw平方根加上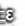
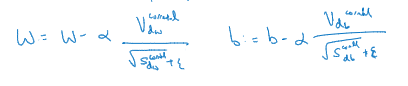
所以Adam算法结合了Momentum和RMSprop梯度下降法，有一种特别常用的算法，能有效适用于不同神经网络，适用于广泛的结构
超参
学习率衰减
加快学习算法的一个办法就是随时间慢慢减少学习率，我们将之称为学习率衰减
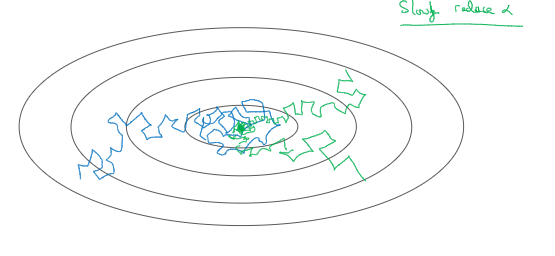
首先通过一个例子了解为啥要计算学习率衰减，假设你要使用mini-batch梯度下降法。mini-batch数量不大，大概64或128个样本，在迭代过程中会有噪音，下降朝向这里的最小值但是不会精确地收敛，所以你的算法最后在附近 摆动。慢慢减少α本质在于在学习初期你能承受较大的步伐，当开始收敛的时候小一些的学习率能让你步伐小一些。可以这样做到学习率衰减
除了这个公式，还有一个叫做指数衰减，其中α相当于一个小于1的值
局部最优的问题
