深度学习的实用层面
训练、开发、测试集
在机器学习中我们通常将样本分成训练集、验证集、和测试集三部分,数据集规模相对较小的适用传统的划分比例;数据规模较大的验证集和测试集可以占到数据总量20%或10%以下
偏差/方差
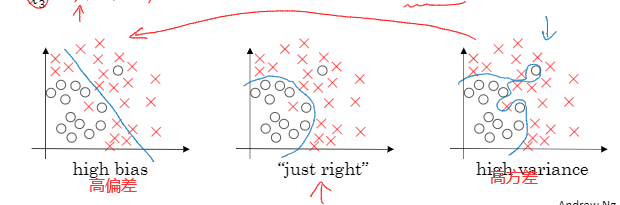
训练集错误率是0.5%,验证集错误率是1%,猫咪分类器只有1%的错误率,偏差和方差都很低。
方差是衡量源数据和期望值相差的度量值。偏差又称为表观误差,是指个别测定值与测定的平均值之差,它可以用来衡量测定结果的精密度高低。

机器学习基础
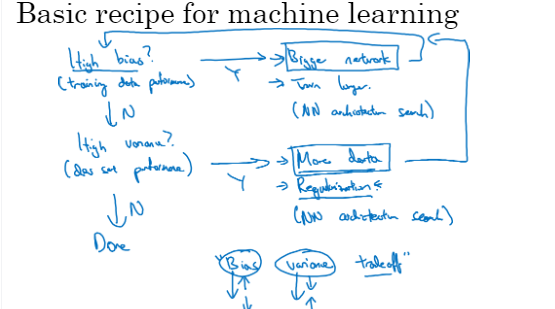
训练神经网络时用到的基本方法,初始模型训练完成后,我首先要知道算法偏差高不高,如果偏差较高,试着评估训练集或训练数据的性能,如果 偏差的确很高,甚至无法拟合训练集,这时我们就需要选择一个新网络,含有更多隐层或者隐藏单元的网络或者花费更多时间来训练网络训练 算法,尝试更先进的优化算法
一旦偏差降低到可接受的数值 ,检查一下方差有没有问题,为了评估方差,我们要查看验证集性能。如果方差高,最好的解决办法就是采用更多数据。我们通常也可以通过正则化来减少拟合。
正则化
如果你怀疑神经网络过度拟合了数据,即存在高方差问题,那么最好的解决方法就是正则化。试着了解一下正则化的原理
我们可以利用逻辑回归来实现这些设想,求成本函数J的最小值,参数包含一些训练 数据和不同数据中个体预测的损失函数,w和b是逻辑回归的两个参数,w是一个多维度参数矢量,b是一个实数,在逻辑回归中加入参数入,也就是正则化参数

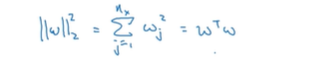 此方法称为L2正则化这里使用了欧几里得法线,被称为向量能数 W的L2范数
此方法称为L2正则化这里使用了欧几里得法线,被称为向量能数 W的L2范数
L1正则化
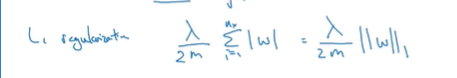

为什么正则化可以减少过拟合
过拟合是指为了得到一致假设而使假设变得过度严格,表示神经网络模型在训练集上的表现很好,但是泛化能力比较差,在测试集上表现不好。
假设这是个庞大的深度拟合神经网络,这个是我们的成本函数J添加正则项,可以避免数据权值矩阵过大
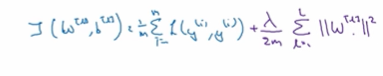 如果正则化入设置得足够大,权重矩阵W被设置为接近于的值,直观理解 就是把多隐藏单元的权重 设为0,于是基本上消除了这些隐藏单元的许多影响,如果是这种情况,这个被大大简化了的神经网络会变成一个很小的网络,小到如同一个逻辑回归单元,可是深度却很大,它会使用这个网络从过拟合的状态,理接近于高偏差状态。但是入会存丰一个中间值,于是会有一个接近just right 的中间状态,直观理解就是入增加到足够大,W会接近于0。我们尝试常消除或至少减少许多隐藏单元的影响,最终 这个网络变得简单,这个神经网络越来越接近逻辑回归
如果正则化入设置得足够大,权重矩阵W被设置为接近于的值,直观理解 就是把多隐藏单元的权重 设为0,于是基本上消除了这些隐藏单元的许多影响,如果是这种情况,这个被大大简化了的神经网络会变成一个很小的网络,小到如同一个逻辑回归单元,可是深度却很大,它会使用这个网络从过拟合的状态,理接近于高偏差状态。但是入会存丰一个中间值,于是会有一个接近just right 的中间状态,直观理解就是入增加到足够大,W会接近于0。我们尝试常消除或至少减少许多隐藏单元的影响,最终 这个网络变得简单,这个神经网络越来越接近逻辑回归
我们再来直观 感受一下正则化为什么可以预防 过拟合。
假设我们用这样的双曲激活函数

那我们发现,只要z非常小,如果z只涉及少量参数,这里我们利用了双曲正切函数的线性状态,只要z可以扩展为这样的更大值或者更小值,激活函数开始变得非线性
如果正则参数入很大,激活函数的参数会相对小,因为代价函数中的参数变大了,如果W很小,z= ,如果w小了,相对于z也会很小,g(z)呈线性,每层几乎都是线性的。如果每一层都是线性网络,那么整个网络就是一个线性网络。
,如果w小了,相对于z也会很小,g(z)呈线性,每层几乎都是线性的。如果每一层都是线性网络,那么整个网络就是一个线性网络。
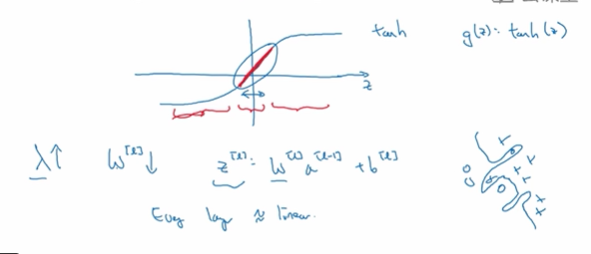
总结一下,如果正则化参数变得很大,参数W很小,z也会变小,这个激活函数会呈线性,整个神经网络会计算离线性函数近的值,不会发生过拟合。
Dropout正则化
除了L2正则化,我们还有一个非常实用的正则化方法是dropout(随机失活)
来个例子,
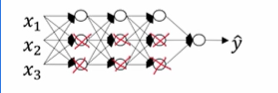
假设我们在训练左图这样的神经网络,它存在过拟合,这就是dropout需要处理的,它会遍历网络的每一层,并设置消除神经网络中节点的概率。
假设网络中的每一层每个节点都以抛硬币的方式设置概率 ,每个节点得以保留和消除的概率都是0.5,设置完节点概率,我们会消除一些节点,然后删除从该节点进出的连线,最后得到一个节点更小规模更小的网络。

如何实施dropout,常用方法 inverted dropout(反向随机失活)
利用三层网络举例说明。首先要定义向量d,d^3表示一个三层的dropout向量,d^3=np.random.rand(a^3.shape)<keep-prob(看它是否小于某数,此为具体数字,上面例子中是0.5,它表示保留某个隐藏单元的概率) 而在此处keep-prob=0.8,它意味着消除任意一个隐藏单元的概率是0.2。它的作用就是生成随机矩阵,其在d^3中的对应值为1的概率都是0.8,其对应值为0的概率是20%,随机数字小于0.8,它等于1的概率是0.8,等于0的概率是0.2。接下来要做的就是从第三层获取激活函数,这里叫它a^3;a^3=np.multply(a^3,d^3),也可以写成a^3*=d^3
它的作用就量过滤d^3中所有等于0的元素,而各个元素等于0的概率只有20%,乘法运算最终把d^3中相应元素归零
最后我们把a^3向外扩展,用它除以0.8,或者除以keep-prob参数;a^3/=keep-prob
其他正则化方法
除了L2正则化和随机失活正则化,还有几种方法可以减少神经网络中的过拟合
假设我们正在拟合猫咪图片分类器,如果你想通过扩增训练数据来解决过拟合,但扩增训练数据代价太高,有时我们无法扩增数据。但我们可以通过添加这类图片来增加训练集,以这种方式扩增算法数据,进而正则化数据集,减少过拟合。

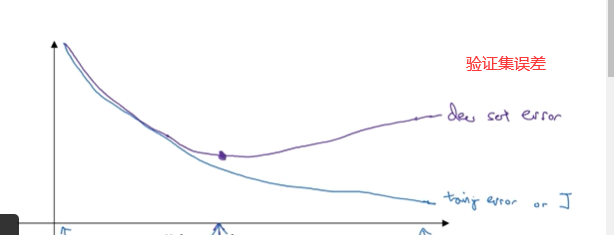
还有另一种常用方法常用的方法叫做early stopping ,运行梯度下降时,我们可以绘制训练误差或只绘制代价函数J的优化过程,通过early stopping 我们不单可以绘制上面这些内容,还可以绘制验证集误差,它可以是验证集上的分类误差。
early stopping发挥的作用是,当你还未在神经网络上运行太多迭代过程的时候,参数W接近0,因为随机初始化W值时它的值可能都是较小的随机值,所以在你长期训练神经网络之前W依然很小,在迭代过程和训练过程中W的值会变得越来越大,这个时候early stopping 要做的就是在中间点停止迭代过程,我们得到一个W值中等大小的弗罗贝尼乌斯范数,与L2正则化相似选择参数W范数较小的神经网络
所以,early stopping 代表的就是提早停止训练神经网络
正则化输入
假设我们有一个训练集,它有两个输入特征,所以输入特征x是二维的,这个是数据集的散点图,归一化输入需要两个步骤:第一步是零均值化;第二步是归一化方差

如果你使用非归一化的输入特征,代价函数就会变得非常细长狭窄的代价函数,最小值在红箭头那儿,如果特征值在不同范围,x1取值范围从1到1000,x2从0到1。这样两个参数值的范围将会非常不同,代价函数会特别狭窄。
如果利用归一化输入的话,代价函数平均起来看更对称。

梯度消失与梯度爆炸
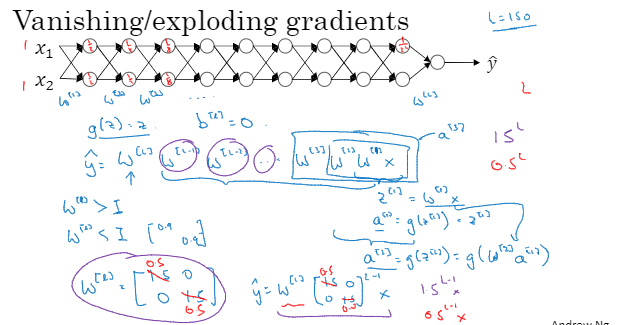
训练神经网络的时候,我们都需要面对一个问题,就是梯度消失与梯度爆炸。也就是说当你训练深度网络时导数坡度有时会变得非常大或小。
这里有一个特别深的神经网络,每层只有两个隐藏单元。我们使用z=g(z)激活函数

神经网络的权重初始化
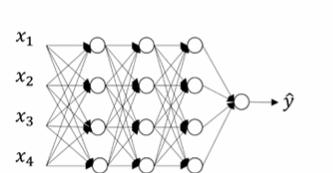
我们来看只有一个神经元的情况,单个神经元有4个输入特征,从x1到x4,经过a=g(z)处理,最终 得到y帽
z= ,为了预防 z值过大或过小,你可以看到n越大,你希望Wi越小,因为z是WiXi的和。如果你把很多此类项相加,希望每项值更小,最合理的方法就是设置Wi=1/n.
,为了预防 z值过大或过小,你可以看到n越大,你希望Wi越小,因为z是WiXi的和。如果你把很多此类项相加,希望每项值更小,最合理的方法就是设置Wi=1/n.
n表示神经元的输入特征数量,实际上我们要做的就是设置某层权重矩阵W

梯度的数值逼近
在实施反向传播时,有一个测试叫作梯度检验,它的作用是确保反向传播正确实施。为了逐渐实现梯度检验,我们需要知道如何 对计算梯度做数值逼近。
我们先画出函数f,标记为f(o),f(o)=o^3

梯度检验
可恶!!!好难啊,听不懂了!!!

