浅层神经网络
神经网络表示
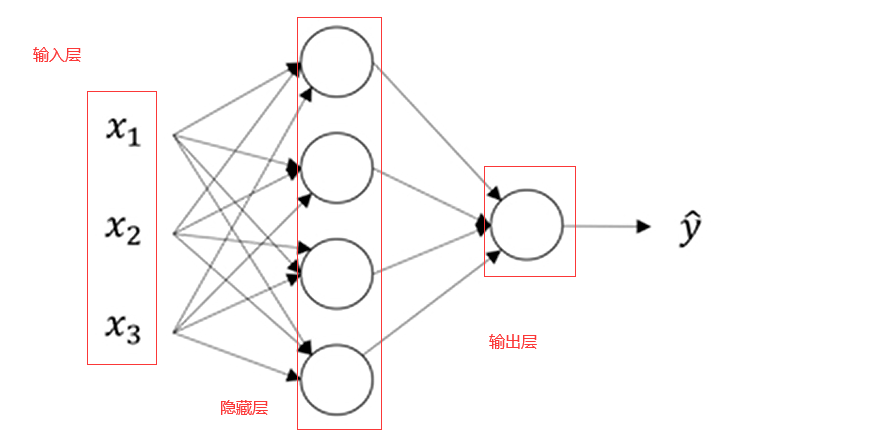
所谓“隐藏”的含义就是在训练集中这些中间节点的真正数值我们是不知道的，在训练集中我们看不到它们的数值。我们能看到输入值，也能看到输出值，但是隐藏层的值我们是无法看到的
之前我们利用x来表示输入特征，现在我们也可以使用
来表示，它意味着网络中不同层的值会传递给后面的层
输入层将x的值传递给隐藏层，我们将输入层的激活值称为a[0]
下一层隐藏层也会产生一些激活值，我们将其记作a[1]
这里的第一个单元或者说节点我们将其表示为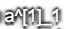
以此类推。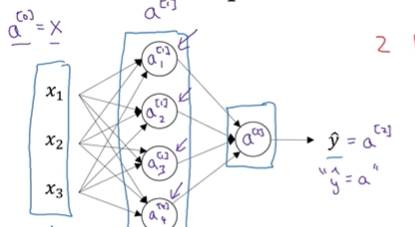
这里是一个四维向量，一个4*1矩阵，所以这个图中有四个节点，或者说四个隐藏层单元。
输出层的话表示的就是a[2]
在此例中这是个双层神经网络。这里不算输入层，隐藏层是第一层
隐藏层有两个相关的参数w和b
计算神经网络的输出
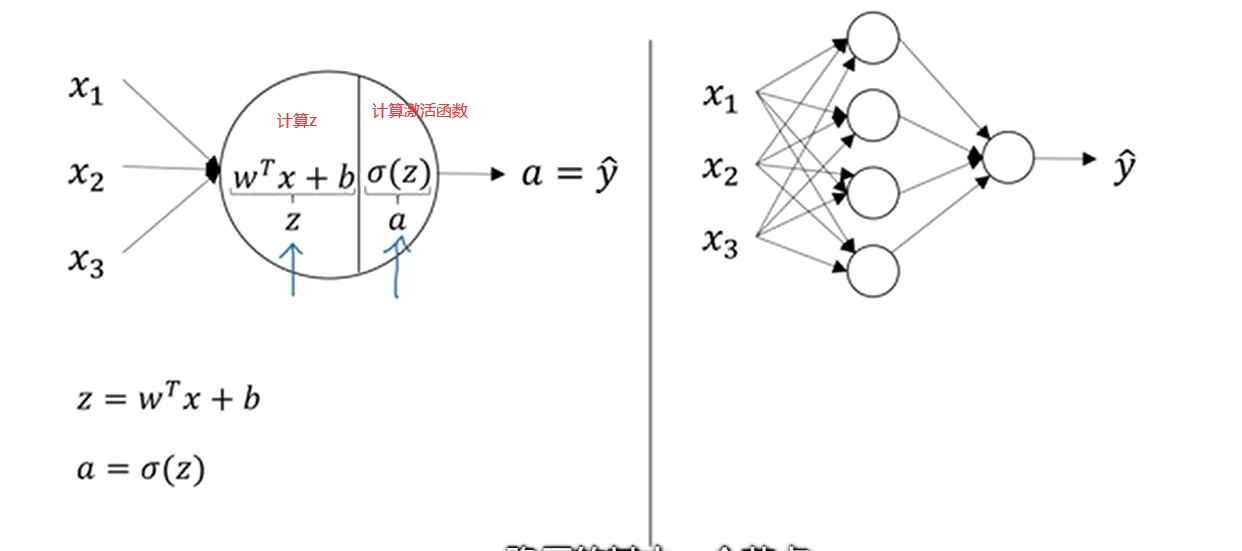
先看左图，这个是logistic回归的计算，分两步，先计算一下z,之后 再计算激活函数也就是sigmoid函数。而右图的神经网络呢就是重复计算这两步骤多次。
只看隐藏层的第一个节点，我们就可以把这个第一个节点看作是左图的这个圆。然后先计算
，这里因为是第一个节点，我们都在符号上面加上一个下标
，之后第二步就是计算激活函数了
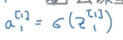
按照之前我们所说的符号第一个节点就写成了a1[1]
上标表示层数；下标表示 层中的第几个节点。
剩下的几个节点也是按照以上方法进行计算。
然后我们可以将它们进行向量化
像这样，之后 ， 我们可以将这些符号w啥的，进行一下堆叠，成为一个w[1]
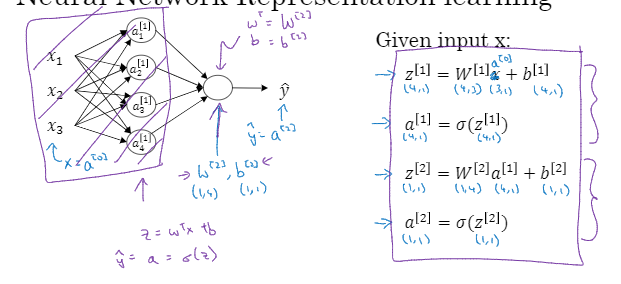
整体来说的话就是，输入一个特征x，然后到隐藏层，先进行两步计算，完了之后 我们到输出层进行计算，输出层计算的话和上面那个左图是一样，也是一个圆，也是分两步进行计算。然后上标就改为[2]即可。所以当我们遇到像这种的神经网络计算单个特征向量时，我们再写代码时只需要写这四步就可以了。
多个例子中的向量化
这个表示第二层的第i 个特征向量
前面有了解到单个特征向量的计算输出。那么如果是有多个呢，无非就是重复几次计算嘛
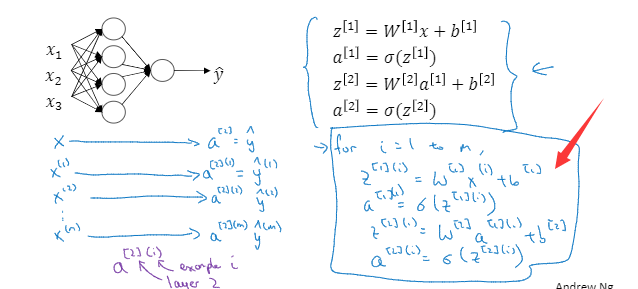
利用for循环来遍历一下。
这些也可以实现向量化
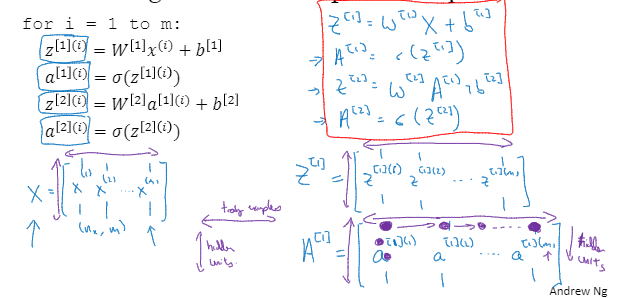
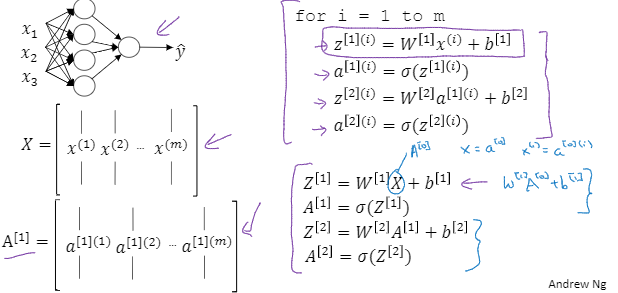
这里就是将一些符号进行了一下堆叠实现向量化
激活函数
在神经网络的正向传播步骤中，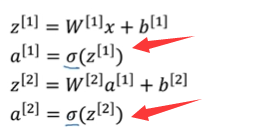
有这两步用的激活函数。这里我们可以使用g来代替
，有一个激活函数效果要比
好一些，就是tanh函数，双曲正切函数。
，介于-1到1之间
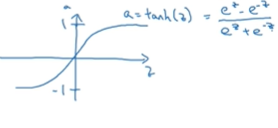
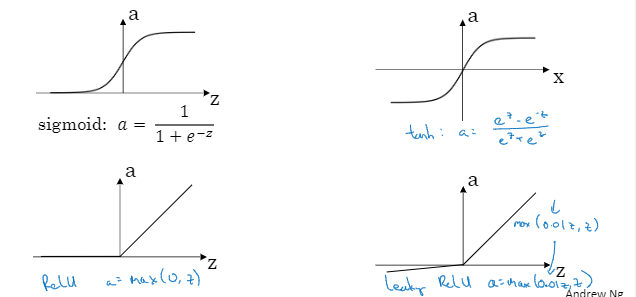
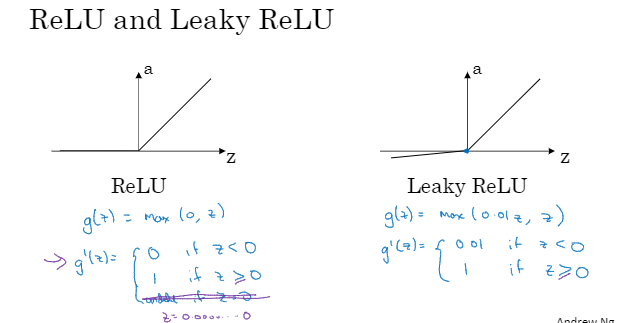
现在函数和tanh函数都有一个缺点就是如果z非常大或非常小，那么导数的梯度或者说这个函数的斜率可能 就很小，所以z很大或很小的时候函数的斜率很接近0，这样会拖慢梯度下降算法。这时，在机器学习里有一个叫修正线性单元，ReLU函数。
只要z为正导数就为1，当z为负的时候，斜率就为0。
在选择激活函数时有一些经验法则，就是如果你在做二元分类，输出值为0和1，那么函数很适合作为输出层的激活函数，然后其他所有单元都有ReLU，如果你不确定隐层应该用哪个，那就可以用ReLU作为激活函数
为什么需要非线性激活函数
事实上，如果你想让你的神经网络能够计算出有趣的函数，那必须使用非线性激活函数。
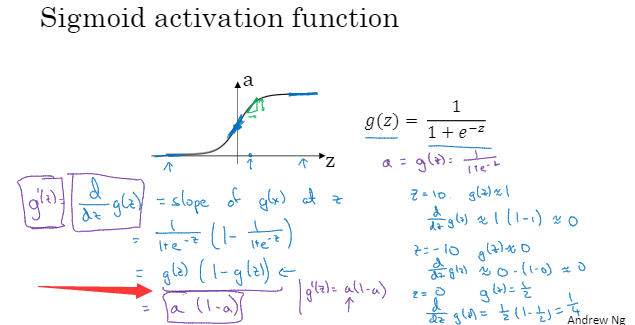
激活函数的导数
神经网络的梯度下降法
单隐层神经网络，有如下参数
使用nx
表示那么多输入特征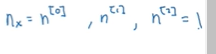
那么矩阵W[1]就是（n[1],n[0]）
b[1]就是n[1]维向量，可以写成（n[1],1）,也就是列向量
b[2]的维度就是（n[2],1）,矩阵W[2]就是（n[2],n[1]）
还有一个神经网络的成本函数：J。假设我们再做二元分类，所以参数就是
J（W[1],b[1],W[2],b[2]）=1/m 然后对损失函数求平均
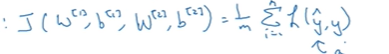
然后这里的L表示 当你的神经网络预测出y帽时的损失函数
所以要训练参数，算法就需要做梯度下降，在训练神经网络时，随机初始化参数很重要
当你把参数初始化成某些值 之后 每个梯度下降循环都会计算预测值
你要计算i=1到m的预测值y帽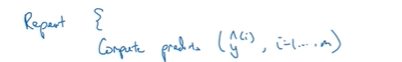
然后计算导数，计算dW[1]，
然后梯度下降最后会更新，将W[1]更新,b[1]也需要更新
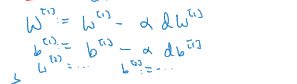
这就是梯度下降的一次迭代循环，然后重复很多次，直到你的参数看起来在收敛
总结一下，正向传播的方程
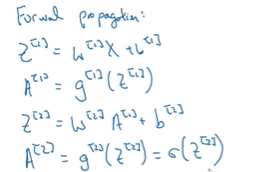
最后这个公式都是对整个训练集向量化，若我们做的是二分分类的话，那么最后这个激活函数应该是sigmoid函数。
轮到反向传播了，也就是计算导数了。
这里运用了一些Python代码，np.sum是python的numpy命令，用来对矩阵的一个维度求和，水平相加求和，而加上开关keepdims就是防止python，直接输出这些古怪的值为1的数组，它的维度是（n,....）,所以加上keepdims=True确保python输出的是矩阵，对于db^[2]这个向量输出的维度是（n,1）
随机初始化
当你训练神经网络时，随机初始化权重非常重要，对于logistic回归可以将权重初始化为零，但如果将神经网络的各参数数组全部初始化为0，再使用梯度下降算法那就完无效了。
当你有两个输入特征，即n^[0]=2，有两个隐藏单元，n^[1]=2;与隐层相关的矩阵W^[1]是2*2的矩阵，是先将值都初始化为0
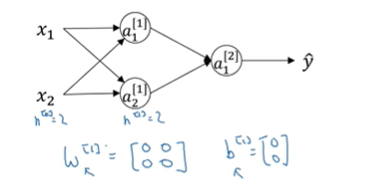
这些初始化的值都是一样的，也就是说两个单元都在做着完全相同的运算，结果也是完全相同的，无论你训练 神经网络多长时间，两个隐藏单元仍然在计算完全一样的函数，所以在这种情况下，多个隐藏单元就没意义了。
所以我们就需要两个不同的隐藏单元去计算不同的函数，解决方案就是随机初始化所有参数。
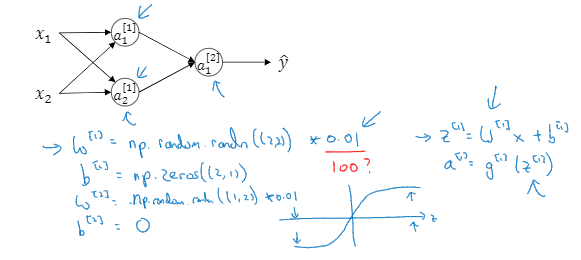
首先我们可以令W^[1]=np.random.randn(2,2)*0.01,这可以产生参数为（2，2）的高斯分布随机变量，然后你再乘以一个很小的数字，比如0.01，这样你就将权重 初始化成很小的随机数。
b的话可以是0的。即b^[1]=np.zero((2,1))
对于W^[2]和b^[2]的话重复上面1的操作就行
