神经网络基础
二分分类
logistic回归是一个用于二分分类的算法。
这里有一个二分分类的例子:
假如有一个图片,内容是一只猫

把这张图片作为我们要输入的内容。想要识别此图的标签,如果是猫的话,就输出 1,如果不是的话就输出0。用变量‘y’来表示输出的标签。
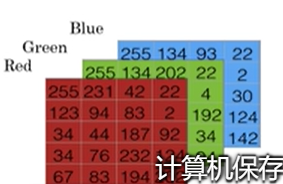
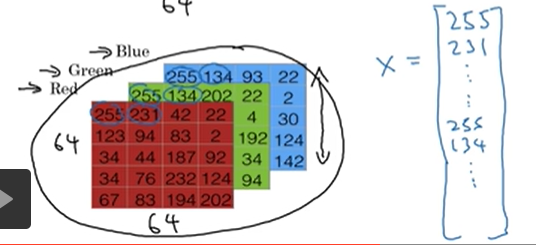
当计算机要保存一张图片的时候,他需要保存三个独立矩阵,分别来对应红、绿、蓝三个颜色通道,假设输入图片是64*64像素的,那么就有三个64*64的矩阵。上述图片表示的只是5*4的。我们要把这些像素亮度都放入一个特征向量x中。用x来表示图片。
(x,y)表示一个单独的样本,x是nx维的特征向量,标签y值为0或1,训练集由m个训练样本构成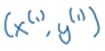 表示样本一的输入和输出。
表示样本一的输入和输出。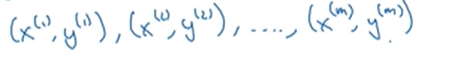 ,这个整体就表示整个训练集。
,这个整体就表示整个训练集。
而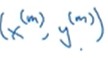 表示最后一样样本m的输入与输出,
表示最后一样样本m的输入与输出, 来表示测试集的样本数。
来表示测试集的样本数。
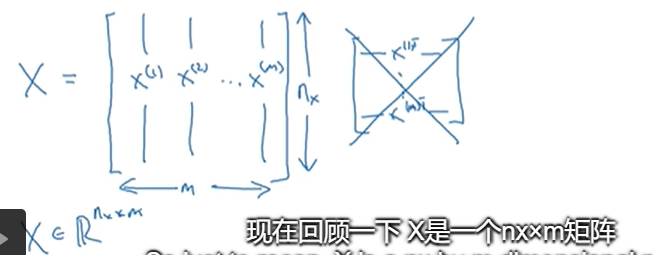
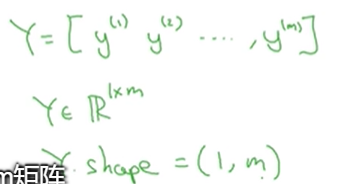
这就是一个1*m矩阵。以上是在logistic回归和神经网络中会用到的符号
logistic回归
logistic回归是一个学习算法,用在监督学习问题中输出y标签是0或1时。是一个二元分类问题
已知输入特征向量x是一张图片,要你识别出来,这是不是猫图,需要运用算法给出一个预测值利用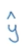 表示y的预测值。
表示y的预测值。 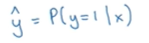 ,当x满足的话,那么y=1。
,当x满足的话,那么y=1。
x是n_x维向量,logistic回归的参数是w也是一个n_x维向量,b是一个实数,如何预测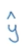 的值。
的值。
这时我们就需要sigmoid函数,以下是sigmoid(z)的图像,用z来表示

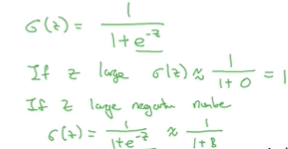
logistic回归损失函数
损失函数也可以叫误差函数,它们可以用来衡量算法的运行情况,你可以定义损失为
与y的差的平方 ,来衡量你的预测输出值
,来衡量你的预测输出值 和y的实际值有多接近。
和y的实际值有多接近。
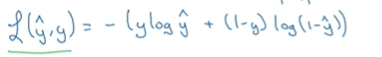

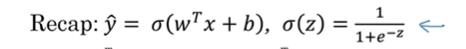
定义一个成本函数J,衡量在全体训练样本上的表现。根据之前得到的两个参数W和b,J(w,b)等于: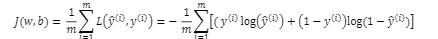
梯度下降法
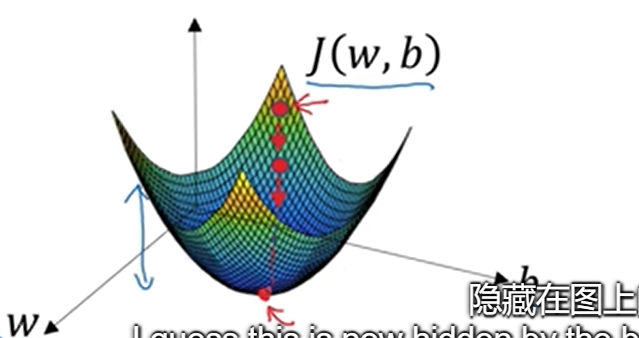
成本函数是一种凸函数。
梯度下降法所做的就是从初始点开始,朝最陡的下坡方向走一步,在梯度下降一步后,可能会在那里停下,因为它正试图沿着最快下降的方向往下走,这是梯度下降的一次迭代,两次迭代或许会到达那里或者多次。
计算图
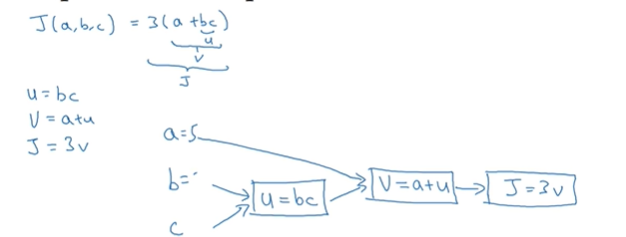
这个是从左到右正向来进行计算的(正向传播)
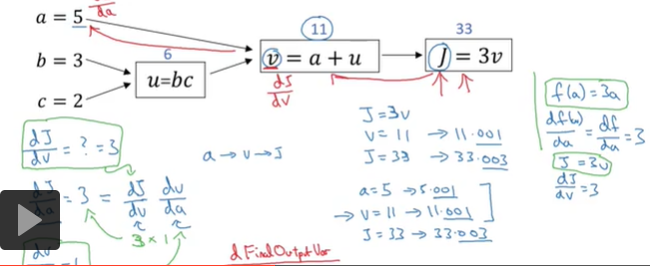
进行求导的话,这个是从右到左反向进行计算的(反向传播)
一个计算流程图,从左到右的进行计算成本函数j,这是正向传播,然后你需要优化函数,反向从右到左计算导数这就是反向传播
logistic回归的梯度下降法

这些是logistic的公式,a是logistic回归的输出 ,y是样本的基本真值标签值,该样本的偏导数流程图如下:假设有两个特征x1,x2.我们为了要计算z,我们需要将w1,w2,b,x1,x2输入
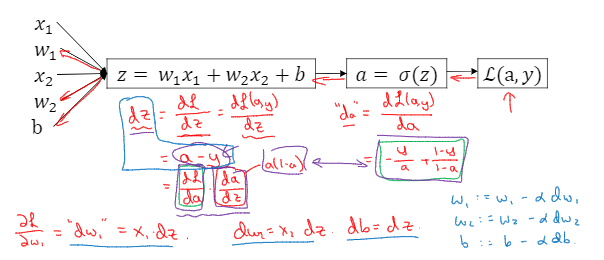
我们在logistic回归中需要做的是变换参数w和b的值,来最小化损失函数,向后计算偏导数。
关于单个样本的梯度下降法,需要做的是使用公式计算dz,dw1,dw2,db;更新w1,w2,b
m个样本的梯度模型
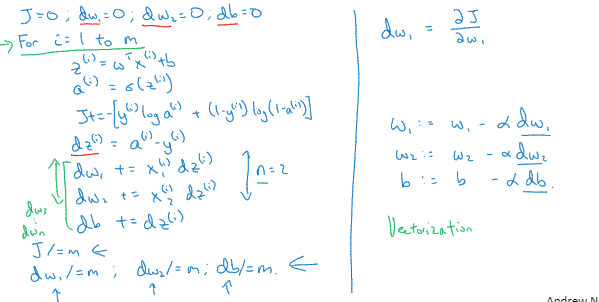
向量化
向量化通常是消除你的代码中显式for循环语句的艺术,在深度学习安全领域、深度学习、练习中经常发现在训练大数据集时,深度学习算法表现才更加优越,所以你的代码运行得非常快很重要,否则它运行在一个大的数据集上面,代码可能会花费很长时间去运行。所以向量化变成一个关键的技巧。
在logistic回归中,我们需要去计算z=w^Tx+b,w是列向量 x也是列向量,它们都是R内的nx维向量
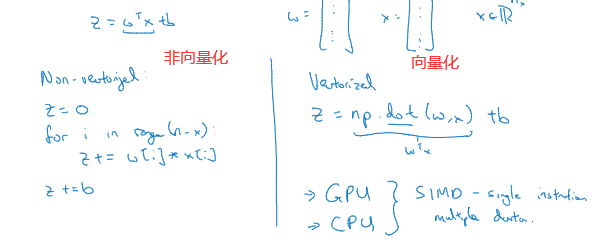
显而易见,向量化十分简洁,能加速我们的代码运行

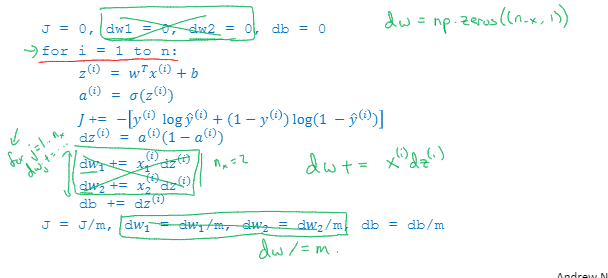
将两个循环简化成一个循环
向量化logistic回归

向量化logistic回归梯度输出
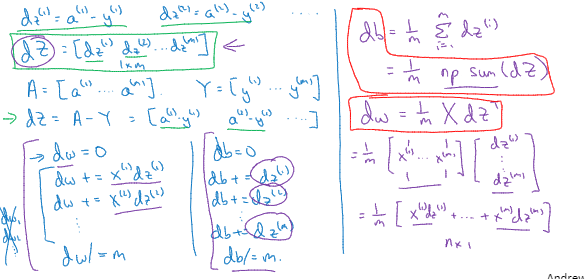
Python中的广播
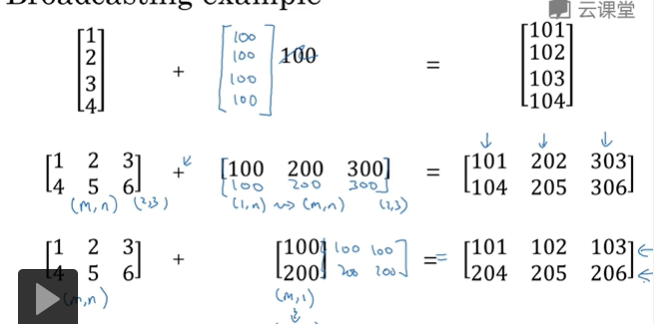
如果有一个m*n的矩阵,进行四则运算与一个1*n矩阵,那么python就会把它复制n次变成m*n矩阵,然后再逐元素做运算;如果相反与一个m*1矩阵进行运算,那么python就会把它复制n次变成m*n矩阵,然后再逐元素做运算
如果有一个m*1的矩阵,这个列向量进行运算与一个实数,把这个实数复制n 次进行运算
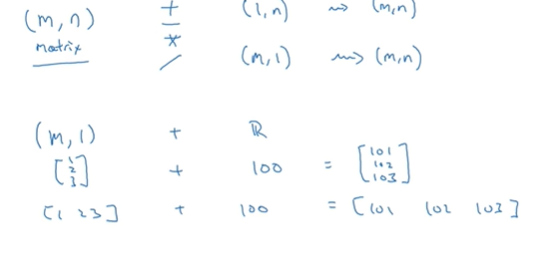


 浙公网安备 33010602011771号
浙公网安备 33010602011771号