一个与 gcd 有关的小结论

原文见http://fuboat.leanote.com/post/share-gcd

我觉得蛮有意思的，就在这里分享给各位。并附上来自同班神犇wuvin的第二种简洁的证法。wuvin的博客    http://wuvin.lofter.com/

因为没有插件，我又是个小白，输入数学符号就显得十分困难，在这里我均引用图片自fuboat的博客，附上我自己的理解

需证明的结论：

对于正整数x,y,n,且x|n,y|n    则

解法一

设 gcd(x,y)=d, 显然有 d|n. 记 n′=n/d,x′=x/d,y′=y/d

则

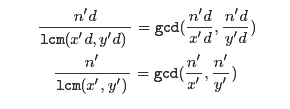
可将原问题转换为规模更小的等价问题，且gcd(x,y)=1.

又x|n,y|n,所以x*y|n ，有

原问题得证

解法二

对于原式，若对每一个n的质因子p^k均成立，则对n成立。

原式转化为证明

　　p^k/ max(p^a,p^b)=min(p^k-b,p^k-a)

不妨设a>=b

则变为求证p^k-a=p^k-a

显然成立