关于复数i本质的探讨
本文参考自:链接
探讨一:
下面来就事论事.
先不谈虚数单位的定义. 我们来看看数系是如何扩充的.
整数抽象自日常的计数. 但是对于"半个馒头"等等的计数问题, 整数无能为力. 把问题精确地写出来, 就是: 多少个(相同的)馒头加在一起是一个馒头? 为此我们需要引入"半个馒头". 换句话说, 我们需要引入方程
[注: 我们觉得有理数很好理解, 不过是因为我们习惯了而已. 数学常常要打破习惯, 从而看到不一样的景色.]
但是有理数究竟是什么? 对于正整数, 我们可以从日常的经验中抽象出来它的性质, 例如说"1是一只羊, 一头牛, 一个人......的共有的数量属性"(这句话本身含义不清楚, 但我们先不去管它). 正的有理数可以通过"等分"来直观地理解. 对于"零"和负数, 这种直观认知就已经有点困难了; 回想一下罗马人是如何对待零的. 为了弥补这种语义上的模糊带来的缺陷, 数学家发明了严格的定义; 下面再讲.
对于无理数, 问题就更加严重, 因为日常计数问题中没有它的对应物. 实际上, 正如我们所知道的, 最早的无理数来源于几何度量问题:
由此立刻产生了问题: 很多具有整系数的二次方程是没有根的(以及更高次的方程). 最简单的例子就是
[由此我们可以看到"为方程寻找根"实际上是一个比"定义圆周率"要抽象得多的问题, 因为后者是"客观存在"的(现在不追究这是什么意思, 下文再讲), 而前者却不一定有什么现实对应物].
我们知道Euler时期就已经对实数有了模糊的概念(他已经发现了很多跟
[这个公式的含义实际上也不明确; 什么叫把
Dedekind等人严格地定义了实数, 至此人们总算是能够用不引发歧义的语言来描述实数. 按照现在的观点, 实数其实也只是一个思维对象, 十进制小数和Dedekind分划等等不过是这个思维对象在现实中的实现. 而圆周率等等需要借助几何度量来定义的实数也可以纳入这个逻辑框架之下了, 因为有了分析学的帮助后, 我们就能够说清楚什么是"曲线的长度"了.
但是对于"虚数", 不得不承认, 我们还是感到困难, 因为它并没有实在的对应物, 可偏偏在实际问题(流体力学, 传热学, 电学etc)之中有着重要的应用.
怎么才能够为方程
我们当然可以通过实数域上的二维可除代数来定义复数. 但这样似乎没法做太多的推广. 所以我们换一种方式来考虑问题. 这种方式能够让我们说清楚什么是"添加代数方程的根".
对于给定的域
[注: 回忆一下, 多项式环
对于一个不可约多项式
这样, 我们知道了"添加代数方程的根"的严格含义. 至于"有理数"的定义, 则要简单得多; 无非就是整环的分式域而已.
如果某域上的任何代数方程在这域中都有解, 则这域称作代数闭的. 对于这类域, 研究其上的多项式是一件比较容易的事情; 实际上, 任何多项式都可以分解成线性因式的乘积(Bezout定理).
回到复数的情形, 取
说了这么多, 才发现自己写了很多似乎很"哲学"的话, 之后后面一部分是干货. 但假如前面的"哲学"能够帮助一些人想清楚问题的话, 我也很欣慰.
拿负数来开平方有必要吗?
有必要!
但是这个问题的完整解答,远不止于“定义:i^2=-1”。
一、笔者首先简要地介绍有理数集:
1、我们有自然数集和加法运算,自然数集对加法运算封闭(两个自然数做加法运算结果还是自然数)。
2、加法运算的逆是减法运算,但是自然数集对减法运算不封闭(不能保证任意两个自然数做减法运算结果还是自然数);通过定义了负数,把自然数集扩充为整数集;整数集对加法运算和减法运算都封闭(人们认可负数经历了很长的过程,原因是认为负数没有现实意义)。
3、乘法运算的逆是除法运算,整数集对乘法运算封闭,但是对除法运算不封闭;通过定义了分数,把整数集扩充为有理数集;有理数集对加法运算、减法运算、乘法运算和除法运算(除数非零)都封闭。
4、有理数集更严格的称谓是“有理数域”,但是“域”的解释需要抽象代数的内容,为了通俗起见,笔者就把“有理数域”称为“有理数集”;以上的“集”都是集合的意思,就是同一类数的集合;比如自然数集、整数集。
二、万物皆数与毕达哥拉斯定理:
1、古希腊时期的毕达哥拉斯学派认为”万物皆数“并奉为教义,这里的数指的是有理数;这种信念源于他们对自己构造的有理数集的自信,他们认为有理数集已经包含了所有的数。
2、随后这个学派发现了”毕达哥拉斯定理“,即”勾股定理“,并用面积法给出了证明。
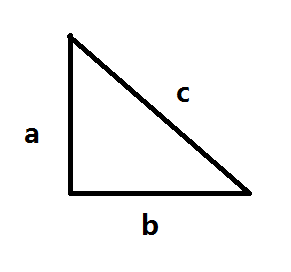
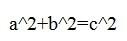
3、如果”万物皆有理数“的话,那么直角三角形的斜边也应该是有理数;但是毕达哥拉斯学派的希帕索斯(Hipasus)找到了这样的例子并给出了证明:a=1,b=1,由a、b通过勾股定理确定的c不是有理数!有一种说法是Hipasus因为这个发现被逐出了学派,另一种说法是他遭到了学派的屠戮。
4、无论如何,有理数集中没有这样”c“,但是现实中确实存在这样的c,那唯一的原因就是毕达哥拉斯学派创造的有理数集存在缺陷,没有涵盖所有的数!
5、通过添加开n次方运算,把有理数集扩充为实集(实集不是实数集,只是部分实数的集合,这里的实集严格来说只是有理数集的n次代数扩张)。
6、实集对加法运算、减法运算、乘法运算和除法运算(除数非零)封闭,实集中的正数还对开n次方运算封闭,实集中的负数对开奇数次方运算封闭而对开偶数次方不封闭;特别的,√(-1)不在这个实集中,换言之在这个实集中没有数的平方等于(-1)。
三、是添加定义的时候了吗?
1、那是否应该添加定义”i^2=-1”或是“i=√(-1)”,把上述的实集做成一个更大的数集?
答案是人们认为没有必要!
2、人们认为正数开方是有意义的,因为开方的结果在现实中有这样的元算与之对应。正如√2,人们确实能找到一条长度不多不少恰好是√2的线段。
3、人们认为负数开方是没有意义的,因为开方的结果在现实中没有这样的元素与之对应。当然笔者还说过,那个时代,人们甚至还不认可负数,因为在现实中没有”负“的线段。³√(-2)=-³√(2)只是正数开方的一种”变形“;至于√(-1),那更没有人关心有没有东西与它对应了,因为它没有现实意义。
四、三次、四次方程与求根公式:
1、所谓的方程,就是含有未知量的等式;未知量是数,方程就是代数方程;未知量是函数,方程就是函数方程(例如微分方程和积分方程);方程的解,就是一个能使方程成立的量;代数方程的解是数,这样的数称为代数方程的根。
2、代数方程里,人们比较关注多项式方程,因为这样的方程与人们的生产生活密切相关;古典数学时期,数学家研究的方程也主要是多项式方程。下文出现的”方程“都特指”多项式方程“。
3、所谓的方程的求根公式,就是用方程的系数通过加减乘除和开方运算来构造根的式子。
4、一次方程和二次方程的求根公式很早就被发现了,人们致力于寻找三次和更高次方程的求根公式。
5、16世纪意大利数学家菲尔洛(Ferro)发现了缺二次项的、即形如x^3+px+q=0的三次方程的求根公式。因为当时人们普遍不接受负数,所以实际上Ferro是把缺二次项的三次方程分成了三类:x^3+px=q、x^3=px+q、x^3+q=px,p和q都是正数;他分别给出了解法。
6、有意思的是,当时的数学家之间流行”决斗“(文艺复兴时期的风气?)。所谓的”决斗“,就是相互要求对手解决自己提出的问题。所以Ferro把自己的三次方程求根公式作为决斗时秘密武器,没有发表。也因为这个求根 公式,Ferro在决斗中屡屡获胜,名声鹊起。
7、Ferro死前,把自己的秘密武器传授给了学生菲奥尔(Fior)和女婿兼继承人纳威(Nave)。
8、Fior也是一个争强好胜的人,他向当时的数学家塔尔塔利亚(Tartaglia,这不是原名,意为口吃者,Tartaglia孩童时期被法国士兵用马刀砍伤了脸变成口吃)提出挑战。Tartaglia并不知道缺二次项的三次方程的求根公式,但是在挑战的压力下,竟然成功地推导出了一般的求根公式!因此,Tartaglia在与Fior的决斗中大获全胜,因为后者并不会解形如x^3+rx^2+px+q=0的一般三次方程。Tartaglia名声鹊起。
9、卡尔丹(Cardano)得知这件事后,多次乞求Tartaglia把求根公式告诉他。作为回报,Cardano许诺给予Tartaglia经济上的援助。Tartaglia最终耐不住Cardano的软磨硬泡和利益诱惑,把求根公式以一首晦涩难懂的语句诗的形式告诉了Cardano,并要求Cardano发誓保密。
10、后来,Cardano从Nave那里了解到Ferro的求根公式,认为Tartaglia的求根公式本质上和Ferro的求根公式是一样的(其实一般的三次方程通过一个变量代换就可以转化为缺二次项的三次方程,待会大家就会看到)。
11、所以Cardano不顾自己的誓言,把求根公式传授给了学生费拉里(Ferrari),Ferrari在此基础上竟然发现了四次方程求根公式!
12、Cardano把三次方程求根公式和学生Ferrari的四次方程求根公式发表在了自己的著作《重要的艺术》(Ars magna)。Cardano这样评论道:”Ferro在30年前就发现了这个法则,并把它传给了Fior。是Fior向Tartaglia挑战,使得Tartaglia有机会重新发现这一法则。Tartaglia在我的恳求之下把这个法则告诉了我,但Tartaglia保留了证明,我在获得这种帮助之下找到了它的证明“。
13、接下来就是Tartaglia对Cardano的严厉控诉,谴责Cardano的背信弃义。愤怒的Tartaglia向Cardano提出挑战,而Ferrari代替自己的老师接收了挑战。因为Ferrari已经发现了四次方程的求根公式,所以大败Tartaglia。Tartaglia名声扫地,在争吵和穷困中度过了晚年。
14、三次方程求根公式是枯燥的,但是公式背后的历史是有趣的;笔者无意评论Cardano和Tartaglia孰对孰错,每个读者心中自有看法。
五、三次方程不可约的情况:
1、一般的三次方程为aX^3+bX2+cX+d=0,通过变量代换X=x-[b/(3a)](前文提及的),一般的三次方程可以转化为缺二次项的三次方程x^3+px+q=0,求解这个方程就可以了。
2、x^3+px+q=0的求根公式:
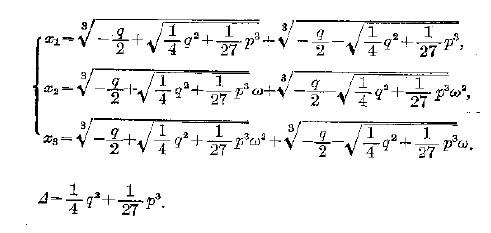
这里笔者就不给出求根公式的推导过程了。
3、注意到⊿要开平方,但⊿并不能保证一定大于0。也就是说,Cardano或是Tartaglia的用加减乘除和开方运算构造的求根公式里,可能要面临负数开平方的困境。
4、为了让读者更清晰的认识到矛盾所在,笔者举一个例子:
三次方程x^3+px+q=0,p=-10,q=6。
函数y=x^3-10x+6的图像大致为
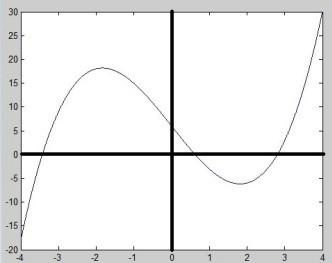
函数曲线和x轴相交的点的x值,就是三次方程x^3-10x+6=0的根。
通过图像,我们可以清楚地看到这个三次方程有3个实根。
但是,⊿=(1/4)q^2+(1/27)p^3=-28.037<0!
5、也就是说,实系数的三次方程,对于⊿<0的情况,为了得到3个实根,根据求根公式,必须对负数开平方!这个结果对16世纪的数学家是难以接受的。
6、借助负数开平方得到实根的过程,实在难以让人满意,所以Cardano试图”修正“求根公式来避免这种情况。但是,所有的尝试都失败。Cardano无奈地把这种情况称为”三次方程不可约“情况。
7、为了处理这种情况,Cardano引入了虚数单位i,定义i^2=-1,使得求根公式可以正常运作。
8、那么这样的”修正“是否存在呢?直到19世纪,天才数学家伽罗瓦(Galois)才用他开创性的群论工具才给出答案:不存在!也就是说:”借助负数开平方得到实根的过程“是无法避免的!
9 、这里必须强调的是:二次方程的求解之所以没有导致虚数i的引入,原因在于判别式⊿<0时方程确实没有实数解,直观地看就是函数曲线y=ax^2+bx+c与x轴确实没有交点,人们不会有兴趣更不会认为有意义而去为负数开平方动脑筋!
六、总结与反思:
1、数学似乎和所有人开了一个玩笑:当你认为有理数域完备的时候,你发现用自己证明的毕达哥拉斯定理居然发现了一大类怪胎,所以不得不把开方运算纳入系统;当你认为求根公式能解决所有三次方程的时候,你发现三个明显存在的实根居然要借助负数开平方,所以不得不定义”i^2=-1”;至于定义了”i^2=-1”之后,给代数和分析带来的诸多便利,那已经是后话。
2、这再次验证了笔者的话:“没有哪一位数学家,可以从一开始就预见他所定义创造的东西,能带来多少方便快捷”,或是存在多少缺陷;数学家都是摸着石头过河,一路上很多修修补补。课本中的斟字酌句的描述,未能表现出创造过程中的斗争、挫折,以及在建立一个客观的结构之前,数学家所经历的艰苦漫长的道路。
3、“i^2=-1”的故事,远不是一个简单的定义所能讲述的.
楼上的答案都没有提到这一点,复数最重要的性质是旋转。也就是两个复数的积的辐角等于各自辐角的和。如果没有这一特性,复数在数学和物理上的地位不会像现在这么重要。
先从原题说起,从根本上来看,为什么i是-1的平方根。
 如上图复数构成一个平面,实轴和虚轴正交。
如上图复数构成一个平面,实轴和虚轴正交。-1位于实轴负半轴,辐角为π(180度)。开平方,按照前面说的辐角的性质,即是辐角减半,变为π/2,也即虚轴正半轴上的i的位置。另一个解是辐角为3π/2的-i,因为-1的辐角也可以是3π。
或者反过来看,一个复数乘以i,就相当于逆时针旋转π/2。那么i^2=1*i*i,就是把1旋转了2次π/2,正好落在-1上。
举一反三,现在大家明白如何从复数旋转的角度,来说明为什么负负得正了吧?
理解了这一点,就很容易明白,为什么复数作为一个不那么自然的,人为发明的数,能够如此好地应用于物理了。
比如极其重要的简谐振动,可以看成复平面单位圆上,做匀速圆周运动的点,在实轴上的投影。既然是旋转,那么用时间的指数函数就可以表达了,并且求导非常方便。
按照i的定义,i是-1的平方根,或者
接着来:
如果你的代数感觉好,你马上就觉得上面的式子有一些“代数味道”。是的,一个角度为
索性,我们把式子补齐:
还记得三角恒等式么:
针对一个任意角度,把cos部分作为实部,把sin部分作为虚部,用三角不等式就可以构造出复数的乘法,这就是复数乘法的意义。改写成:
也就是教科书上看到的形式:
如果你有兴趣,请玩欧拉公式,去了解这种乘法计算中的各种有趣的地方。
至于i么,其实就是复平面上的一个自然基。i的“全称”是:
小结一下:在实数上玩的时候(比如代数多项式的根),常常发现数不够用,于是把实数扩张成复平面。复数(域)的运算限制在实轴(域)上都是成立的。i的平方所以是-1,这样理解:平方是同一变换两次合成的结果。把实数乘法单位元1变换成-1(加法群逆元),需要在复数域中表达为一个角度为
我们刚才都是从代数在讲。我们注意从分析上:
各种导数,都无非是在相位上变换;欧拉公式也能看出,乘除和指对数也都是在相位上变换;就不难理解为什么那么多物理现象需要用复数来描述了。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号