DP Intro - OBST

 

http://radford.edu/~nokie/classes/360/dp-opt-bst.html

 

Overview

---

Optimal Binary Search Trees - Problem

• Problem:
• Sorted set of keys k1,k2,...,knk1,k2,...,kn

 

• Key probabilities: p1,p2,...,pnp1,p2,...,pn

 

• What tree structure has lowest expected cost?

 

• Cost of searching for node ii : cost(ki)=depth(ki)+1cost(ki)=depth(ki)+1

Expected Cost of tree =∑i=1ncost(ki)pi=∑i=1n(depth(ki)+1)pi=∑i=1ndepth(ki)pi+∑i=1npi=(∑i=1ndepth(ki)pi)+1Expected Cost of tree =∑i=1ncost(ki)pi=∑i=1n(depth(ki)+1)pi=∑i=1ndepth(ki)pi+∑i=1npi=(∑i=1ndepth(ki)pi)+1

---

Optimal BST - Example

• Example:
• Probability table (pipi is the probabilty of key kiki :

ii	1	2	3	4	5
kiki	k1k1	k2k2	k3k3	k4k4	k5k5
pipi	0.25	0.20	0.05	0.20	0.30

Two BSTs
• Given: k1<k2<k3<k4<k5k1<k2<k3<k4<k5

 

• Tree 1:
• k2/[k1,k4]/[nil,nil],[k3,k5]k2/[k1,k4]/[nil,nil],[k3,k5]
• cost = 0(0.20) + 1(0.25+0.20) +2(0.05+0.30) + 1 = 1.15 + 1

 

• Tree 2:
• k2/[k1,k5]/[nil,nil],[k4,nil]/[nil,nil],[nil,nil],[k3,nil],[nil,nil]k2/[k1,k5]/[nil,nil],[k4,nil]/[nil,nil],[nil,nil],[k3,nil],[nil,nil]
• cost = 0(0.20) + 1(0.25+0.30) +2(0.20) + 3(0.05) + 1 = 1.10 + 1

 

• Notice that a deeper tree has expected lower cost

---

Optimal BST - DP Approach

• Optimal BST TT must have subtree T′T′ for keys ki…kjki…kj which is optimal for those keys
• Cut and paste proof: if T′T′ not optimal, improving it will improve TT , a contradiction

 

• Algorithm for finding optimal tree for sorted, distinct keys ki…kjki…kj :
• For each possible root krkr for i≤r≤ji≤r≤j
• Make optimal subtree for ki,…,kr−1ki,…,kr−1
• Make optimal subtree for kr+1,…,kjkr+1,…,kj
• Select root that gives best total tree

 

• Formula: e(i,j)e(i,j) = expected number of comparisons for optimal tree for keys ki…kjki…kj

e(i,j)={0, if i=j+1mini≤r≤j{e(i,r−1)+e(r+1,j)+w(i,j)}, if i≤je(i,j)={0, if i=j+1mini≤r≤j{e(i,r−1)+e(r+1,j)+w(i,j)}, if i≤j

• where w(i,j)=∑k=ijpiw(i,j)=∑k=ijpi is the increase in cost if ki…kjki…kj is a subtree of a node

• Work bottom up and remember solution

---

Optimal BST - Algorithm and Performance

• Brute Force: try all tree configurations
• Ω(4ⁿ / n^3/2) different BSTs with n nodes

 

• DP: bottom up with table: for all possible contiguous sequences of keys and all possible roots, compute optimal subtrees

    for size in 1 .. n loop             -- All sizes of sequences
        for i in 1 .. n-size+1 loop     -- All starting points of sequences
            j := i + size - 1
            e(i, j) := float'max;
            for r in i .. j loop        -- All roots of sequence ki .. kj
                t := e(i, r-1) + e(r+1, j) + w(i, j)
                if t < e(i, j)  then
                    e(i, j) := t
                    root(i, j) := r
                end if
            end loop
        end loop
    end loop
    

• Θ(n³)

 

• Can, of course, also use (memoized) recursion

 

 

 

http://www.geeksforgeeks.org/dynamic-programming-set-24-optimal-binary-search-tree/

 

Dynamic Programming | Set 24 (Optimal Binary Search Tree)

Given a sorted array keys[0.. n-1] of search keys and an array freq[0.. n-1] of frequency counts, where freq[i] is the number of searches to keys[i]. Construct a binary search tree of all keys such that the total cost of all the searches is as small as possible.

Let us first define the cost of a BST. The cost of a BST node is level of that node multiplied by its frequency. Level of root is 1.

Example 1
Input:  keys[] = {10, 12}, freq[] = {34, 50}
There can be following two possible BSTs 
        10                       12
          \                     / 
           12                 10
          I                     II
Frequency of searches of 10 and 12 are 34 and 50 respectively.
The cost of tree I is 34*1 + 50*2 = 134
The cost of tree II is 50*1 + 34*2 = 118 

Example 2
Input:  keys[] = {10, 12, 20}, freq[] = {34, 8, 50}
There can be following possible BSTs
    10                12                 20         10              20
      \             /    \              /             \            /
      12          10     20           12               20         10  
        \                            /                 /           \
         20                        10                12             12  
     I               II             III             IV             V
Among all possible BSTs, cost of the fifth BST is minimum.  
Cost of the fifth BST is 1*50 + 2*34 + 3*8 = 142

1) Optimal Substructure:
The optimal cost for freq[i..j] can be recursively calculated using following formula.

We need to calculate optCost(0, n-1) to find the result.

The idea of above formula is simple, we one by one try all nodes as root (r varies from i to j in second term). When we make rth node as root, we recursively calculate optimal cost from i to r-1 and r+1 to j.
We add sum of frequencies from i to j (see first term in the above formula), this is added because every search will go through root and one comparison will be done for every search.

2) Overlapping Subproblems
Following is recursive implementation that simply follows the recursive structure mentioned above.

// A naive recursive implementation of optimal binary search tree problem
#include <stdio.h>
#include <limits.h>

// A utility function to get sum of array elements freq[i] to freq[j]
int sum(int freq[], int i, int j);

// A recursive function to calculate cost of optimal binary search tree
int optCost(int freq[], int i, int j)
{
   // Base cases
   if (j < i)      // If there are no elements in this subarray
     return 0;
   if (j == i)     // If there is one element in this subarray
     return freq[i];

   // Get sum of freq[i], freq[i+1], ... freq[j]
   int fsum = sum(freq, i, j);

   // Initialize minimum value
   int min = INT_MAX;

   // One by one consider all elements as root and recursively find cost
   // of the BST, compare the cost with min and update min if needed
   for (int r = i; r <= j; ++r)
   {
       int cost = optCost(freq, i, r-1) + optCost(freq, r+1, j);
       if (cost < min)
          min = cost;
   }

   // Return minimum value
   return min + fsum;
}

// The main function that calculates minimum cost of a Binary Search Tree.
// It mainly uses optCost() to find the optimal cost.
int optimalSearchTree(int keys[], int freq[], int n)
{
     // Here array keys[] is assumed to be sorted in increasing order.
     // If keys[] is not sorted, then add code to sort keys, and rearrange
     // freq[] accordingly.
     return optCost(freq, 0, n-1);
}

// A utility function to get sum of array elements freq[i] to freq[j]
int sum(int freq[], int i, int j)
{
    int s = 0;
    for (int k = i; k <=j; k++)
       s += freq[k];
    return s;
}

// Driver program to test above functions
int main()
{
    int keys[] = {10, 12, 20};
    int freq[] = {34, 8, 50};
    int n = sizeof(keys)/sizeof(keys[0]);
    printf("Cost of Optimal BST is %d ", optimalSearchTree(keys, freq, n));
    return 0;
}

Output:

Cost of Optimal BST is 142

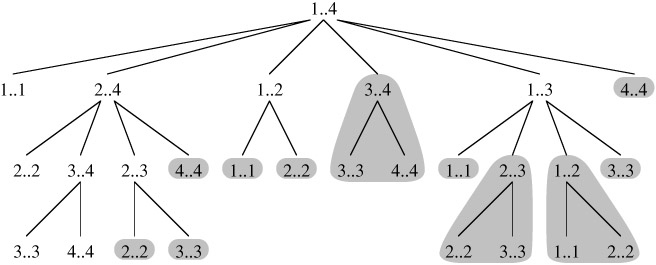
Time complexity of the above naive recursive approach is exponential. It should be noted that the above function computes the same subproblems again and again. We can see many subproblems being repeated in the following recursion tree for freq[1..4].

Since same suproblems are called again, this problem has Overlapping Subprolems property. So optimal BST problem has both properties (see this and this) of a dynamic programming problem. Like other typical Dynamic Programming(DP) problems, recomputations of same subproblems can be avoided by constructing a temporary array cost[][] in bottom up manner.

Dynamic Programming Solution
Following is C/C++ implementation for optimal BST problem using Dynamic Programming. We use an auxiliary array cost[n][n] to store the solutions of subproblems. cost[0][n-1] will hold the final result. The challenge in implementation is, all diagonal values must be filled first, then the values which lie on the line just above the diagonal. In other words, we must first fill all cost[i][i] values, then all cost[i][i+1] values, then all cost[i][i+2] values. So how to fill the 2D array in such manner> The idea used in the implementation is same as Matrix Chain Multiplication problem, we use a variable ‘L’ for chain length and increment ‘L’, one by one. We calculate column number ‘j’ using the values of ‘i’ and ‘L’.

// Dynamic Programming code for Optimal Binary Search Tree Problem
#include <stdio.h>
#include <limits.h>

// A utility function to get sum of array elements freq[i] to freq[j]
int sum(int freq[], int i, int j);

/* A Dynamic Programming based function that calculates minimum cost of
   a Binary Search Tree. */
int optimalSearchTree(int keys[], int freq[], int n)
{
    /* Create an auxiliary 2D matrix to store results of subproblems */
    int cost[n][n];

    /* cost[i][j] = Optimal cost of binary search tree that can be
       formed from keys[i] to keys[j].
       cost[0][n-1] will store the resultant cost */

    // For a single key, cost is equal to frequency of the key
    for (int i = 0; i < n; i++)
        cost[i][i] = freq[i];

    // Now we need to consider chains of length 2, 3, ... .
    // L is chain length.
    for (int L=2; L<=n; L++)
    {
        // i is row number in cost[][]
        for (int i=0; i<=n-L+1; i++)
        {
            // Get column number j from row number i and chain length L
            int j = i+L-1;
            cost[i][j] = INT_MAX;

            // Try making all keys in interval keys[i..j] as root
            for (int r=i; r<=j; r++)
            {
               // c = cost when keys[r] becomes root of this subtree
               int c = ((r > i)? cost[i][r-1]:0) + 
                       ((r < j)? cost[r+1][j]:0) + 
                       sum(freq, i, j);
               if (c < cost[i][j])
                  cost[i][j] = c;
            }
        }
    }
    return cost[0][n-1];
}

// A utility function to get sum of array elements freq[i] to freq[j]
int sum(int freq[], int i, int j)
{
    int s = 0;
    for (int k = i; k <=j; k++)
       s += freq[k];
    return s;
}

// Driver program to test above functions
int main()
{
    int keys[] = {10, 12, 20};
    int freq[] = {34, 8, 50};
    int n = sizeof(keys)/sizeof(keys[0]);
    printf("Cost of Optimal BST is %d ", optimalSearchTree(keys, freq, n));
    return 0;
}

Output:

Cost of Optimal BST is 142

Notes
1) The time complexity of the above solution is O(n^4). The time complexity can be easily reduced to O(n^3) by pre-calculating sum of frequencies instead of calling sum() again and again.

2) In the above solutions, we have computed optimal cost only. The solutions can be easily modified to store the structure of BSTs also. We can create another auxiliary array of size n to store the structure of tree. All we need to do is, store the chosen ‘r’ in the innermost loop.

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.