EK算法求最大流

题目

【模板】网络最大流

题目描述

如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。

输入格式

第一行包含四个正整数 \(n,m,s,t\)，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来 \(m\) 行每行包含三个正整数 \(u_i,v_i,w_i\)，表示第 \(i\) 条有向边从 \(u_i\) 出发，到达 \(v_i\)，边权为 \(w_i\)（即该边最大流量为 \(w_i\)）。

输出格式

一行，包含一个正整数，即为该网络的最大流。

样例 #1

样例输入 #1

4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40

样例输出 #1

50

提示

样例输入输出 1 解释

题目中存在 \(3\) 条路径：

• \(4\to 2\to 3\)，该路线可通过 \(20\) 的流量。
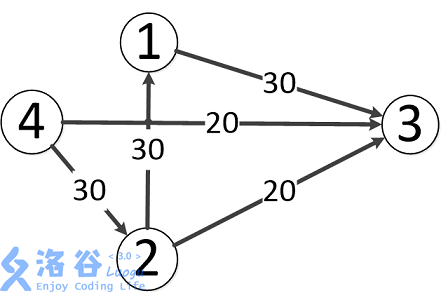
• \(4\to 3\)，可通过 \(20\) 的流量。
• \(4\to 2\to 1\to 3\)，可通过 \(10\) 的流量（边 \(4\to 2\) 之前已经耗费了 \(20\) 的流量）。

故流量总计 \(20+20+10=50\)。输出 \(50\)。

---

数据规模与约定

• 对于 \(30\%\) 的数据，保证 \(n\leq10\)，\(m\leq25\)。
• 对于 \(100\%\) 的数据，保证 \(1 \leq n\leq200\)，\(1 \leq m\leq 5000\)，\(0 \leq w\lt 2^{31}\)。

代码

// 最大流最小割定理：(1) 可以流f是最大流(2) 可行流f的残留网络中不存在增广路(3) 存在某个割[S, T]，|f| = c(S, T)
//EK算法基于 可行流f的残留网络中不存在增广路
#include<bits/stdc++.h>
#define pii pair <int, int>
#define pll pair <ll, ll>
#define endl '\n'
#define il inline
#define pb push_back
#define fi first
#define se second
#define lc u<<1
#define rc u<<1|1
using namespace std;
typedef long long ll;
const int INF=0x3f3f3f3f;
const int N=2e2+10,M=1e4+10;
int h[N],e[M],ne[M],f[M],idx;//前向星，f表示容量
int n,m,S,T;//点数边数，起点终点
int q[N],d[N],pre[N];//q：找增广路时宽搜所用队列，d[i]：走到i点时流量的限制，pre记录前驱边，用于更新残留网络
bool st[N];//防止重复搜索
void add(int a,int b,int c)
{
	e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++;//加入正向边，存储容量
	e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++;//加反向边，初始流量为0
}
void remake()
{

};
bool bfs()
{
	
	int hh=0,tt=0;//宽搜初始化
	memset(st,false,sizeof st);
	q[0]=S,st[S]=true,d[S]=INF;//起点没有限制
	while(hh<=tt)
	{
		int t=q[hh++];
		for(int i=h[t];~i;i=ne[i])
		{
			int ver=e[i];
			if(!st[ver]&&f[i])//没有访问过并且流量大于0
			{
				st[ver]=true;//标记
				d[ver]=min(d[t],f[i]);//更新容量限制
				pre[ver]=i;//记录前驱边
				if(ver==T)return true;//找到增广路则返回
				q[++tt]=ver;
			}
		}
	}
	return false;
}
ll EK()
{
	ll r=0;
	while(bfs())//如果存在增广路
	{
		r+=d[T];//增加流量
		for(int i=T;i!=S;i=e[pre[i]^1])//依次更新前驱边的流量
		f[pre[i]]-=d[T],f[pre[i]^1]+=d[T];
	}
	return r;//返回最大流
}
int main()
{
	cin>>n>>m>>S>>T;
	memset(h,-1,sizeof h);
	while(m--)
	{
		int a,b,c;
		cin>>a>>b>>c;
		add(a,b,c);
	}
	cout<<EK()<<endl;
  return 0;
}