Codeforces Round 993 (Div. 4)题解
Codeforces Round 993 (Div. 4)
现在div4出那么难干嘛...
A. Easy Problem
输入一个数n，返回有多少组正整数(a,b) 满足\(a+b=n\)。
每个数可以选择[1,n-1]共计n-1对。
void solve()
{
int n = 0;
cin >> n;
cout << n - 1 << endl;
}
玻璃上正面写一串pqw组成的字符串，输出背面看过去的字符串
翻转字符串，然后还要把pq对应替换
void solve()
{
string s;
cin >> s;
reverse(s.begin(), s.end());
for (auto& v : s) {
if (v == 'p') v = 'q';
else if (v == 'q') v = 'p';
}
cout << s << endl;
}
有两排m个座位安排给猴子坐，a个猴子只能坐第一排，b个猴子只能做第二排，c个猴子都可以。问最多安排多少个猴子坐下
贪心 第一排坐 min(m,a)个，第二排坐min(m,b)个，然后剩下的尽量放c
void solve()
{
int m, a, b, c;
cin >> m >> a >> b >> c;
int c1 = min(m, a);
int c2 = min(m, b);
int c3 = min(m - c1 + m - c2, c);
cout << c1 + c2 + c3 << endl;
}
给定长度为n的数组A，\(1<=A_i<=n\)，要求构建数组B，满足每个\(A_i\)是区间\([B_1-B_i]\)的众数(或之一)
比如A=[1,1,2]，则B可以是[1,2,2]
由于只要满足是众数之一即可，显然可以构建B为一个n的排列即可，每个数字出现次数都是1，只需要在\(A_i\)出现的时B中已经出现过\(A_i\)即可。
处理时要做到，每个\(A_i\)出现时B数组中\(i\)之前已经出现过\(A_i\)，还得注意\(i\)之后出现的\(A_i\)不能在B中使用。
那么可以在每个数字v首次出现的位置直接标记\(ans[i]=v\)，然后标记v已经使用\(flag[v]=1\)。
然后从头遍历ans中为标记的位置，另一个指针就从1开始累加，找到第一个flag[v]为标记的数字赋值即可。
void solve()
{
int n; cin >> n;
vector<int> flag(n + 1);
vector<int> ans(n);
for (int i = 0; i < n; i++) {
int v; cin >> v;
if (!flag[v]) {
flag[v] = 1;
ans[i] = v;
}
}
int now = 1;
for (int i = 0; i < n; i++) {
if (ans[i] == 0) {
while (flag[now]) now++;
ans[i] = now++;
}
}
for (int i = 0; i < n; i++) cout << ans[i] << " ";
cout << endl;
}
给定\(k,x1,x2,y1,y2\)，要求统计\((x,y)\)数对个数，要求满足
\(x1<=x<=x2\)
\(y1<=y<=y2\)
\(y/x=k^n\) 这条意思是\(y/x\)是k的某个幂。比如k=2,y=8,x=2,则\(y/x=4=2^2\)，注意\(y/x\)必须是整除
这里n可以为0，考虑n=0的情况，此时\(x=y\)，即求[x1,x2]和[y1,y2]的重叠区间
求重叠区间有个常识做法，即重叠部分区间设为[L,R]，则有
\(L=max(x1,y1)\)
\(R=min(yx,y2)\)
如果\(L>R\)则无重叠部分。
由于n为指数，可以暴力枚举n∈[0,60]，对于n>0的情况，考虑x的值域，类似地，有
设\(r=k^n\)
\(L=max(x1,(y1+r-1)/r)\) 注意在x值域中，要取能>=y1的x值
\(R=min(x2,y2/r)\)
void solve()
{
long k, x1, x2, y1, y2;
cin >> k >> x1 >> x2 >> y1 >> y2;
long ans = 0;
for (int n = 0; n <= 60; n++) {
long r = pow(k, n);
if (r * x1 > y2) break;
ans += max(0L, min(x2, y2 / r) - max(x1, (y1 + r - 1) / r) + 1);
}
cout << ans << endl;
}
给定n长度数组A，m长度数组B，n*m矩阵的每一项为\(A_i*B_j\)，设矩阵元素和为\(S=\sum_{i=1}^{n}\sum_{j=1}^{m}A_i*B_j\)。
你可以在一次操作中，可以将M某一行和某一列同时设置为0。
有q次查询，每次查询给出一个整数\(x_i\)，问能否通过一次操作使得矩阵元素和\(S=x_i\)，每次查询独立。
1<=n,m,x<=2e5
认真思考这个数据范围，n，m均为2e5，且没有标准n*m的范围，说明实际上无法枚举整个矩阵。只能单独枚举AB数组。
而x<=2e5，启发我们通过x的值处理。
在无操作的时候有\(S=\sum A*\sum B\)。而一次操作实际上对应了从AB中各删除一个数据后的结果。即
\(x_i=(\sum A-x) * (\sum B-y)\)
请务必意识到这是一个将整数\(x_i\)分解因子的式子
具体来说，预处理所有的\((\sum A - x)\)和\((\sum B - y)\) 存入哈希表
分解\(x_i\)，对于每组因子，计算能否一一对应。
注意\(x_i\)可能为负数，且分解也有正负两种情况，以及互换AB的可能。
unordered_set会被卡哈希，不行就数组吧，或者自定义哈希函数。
void solve()
{
i64 n, m, q; cin >> n >> m >> q;
i64 sumA = 0, sumB = 0;
vector<i64> A(n);
for (int i = 0; i < n; i++) cin >> A[i], sumA += A[i];
vector<i64> B(m);
for (int i = 0; i < m; i++) cin >> B[i], sumB += B[i];
set<i64> setA, setB;
for (int i = 0; i < n; i++) setA.insert(sumA - A[i]);
for (int i = 0; i < m; i++) setB.insert(sumB - B[i]);
auto dfs = [&](i64 x) -> bool {
if (x == 0) {
if (setA.count(0) || setB.count(0)) return true;
}
i64 y = abs(x);
for (int i = 1; i <= y / i; i++) {
if (y % i == 0) {
if (setA.count(i) && setB.count(x / i)) return true;
if (setA.count(-i) && setB.count(-x / i)) return true;
if (setB.count(i) && setA.count(x / i)) return true;
if (setB.count(-i) && setA.count(-x / i)) return true;
}
}
return false;
};
while (q-- > 0) {
i64 x; cin >> x;
if (dfs(x)) cout << "YES" << endl;
else cout << "NO" << endl;
}
}
G1. Medium Demon Problem (easy version)
给定长为n的数组，每个元素\(a_i\)表示有一条从\(i->a_i\)的有向边，初始每个节点拥有一个礼物，每一轮每个节点会向子节点派发这个礼物。如果某个节点拥有超过1个，会立即变为1个。所有的派发同时发生。
问最少经过多少轮，所有节点的礼物数不再发生变化。
翻译完其实是很明显的内向基环树
然后求的是不在环上的点，距离环的最远距离。普通模拟大致是求出所有环上节点，然后倒序BFS查找最远距离。
第一轮是初始状态，经过最远的链的长度轮数后，到达环上，然后下一轮开始循环。
还是给个简易示意图。如下，节点9的礼物经过最多轮数到达环上，9->8->7->1，所以答案是3+2=5。
更简洁的做法是拓扑排序计算拓扑轮数即可。
特别注意，环上延伸出来的并非是一定是链，也可能是树，注意始终取子树里的最长链
void solve()
{
int n; cin >> n;
vector<int> deg(n);
vector<int> fa(n);
for (int u = 0; u < n; u++) {
int v; cin >> v;
v--;
deg[v]++;
fa[u] = v;
}
int step = 2;
queue<int> queue;
for (int i = 0; i < n; i++) if (deg[i] == 0) queue.push(i);
while (queue.size() > 0) {
int size = queue.size();
while (size-- > 0) {
int u = queue.front();
queue.pop();
int v = fa[u];
deg[v]--;
if (deg[v] == 0) queue.push(v);
}
step++;
}
cout << step << endl;
}
G2. Medium Demon Problem (hard version)
与G1的区别在于 过程中节点个数可以>1，而每次只能向上派发一个，所以需要把当前节点所有子树下的礼物逐个派发完成才行
所以向上返回时需要附加当前子树size。
void solve()
{
int n; cin >> n;
vector<int> deg(n);
vector<int> fa(n);
for (int u = 0; u < n; u++) {
int v; cin >> v;
v--;
deg[v]++;
fa[u] = v;
}
queue<int> queue;
vector<int> gifts(n);
for (int i = 0; i < n; i++) {
if (deg[i] == 0) queue.push(i);
gifts[i] = 1;
}
int ans = 0;
while (queue.size() > 0) {
int size = queue.size();
while (size-- > 0) {
int u = queue.front();
ans = max(ans, gifts[u]);
queue.pop();
int v = fa[u];
deg[v]--;
gifts[v] += gifts[u];
if (deg[v] == 0) queue.push(v);
}
}
cout << ans + 2 << endl;
}
基环树只有一个环
拓扑排序的处理过程中 依然可以计算子树size并向上返回，但是处理顺序是拓扑排序的顺序。
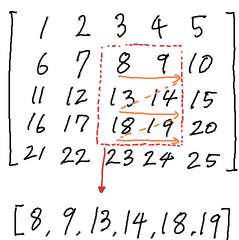
给定n行m列的矩阵，q个查询，每个查询里选择矩阵里的子区域，[x1,x2,y1,y2]，然后把子区域扁平化为一个数组A
可知数组长度为\(c=(x2-x1+1)*(y2-y1+1)\)
计算\(\sum_{i=1}^{c}A_i*i\)
此处必须附上出题人的灵魂画图：
这很Educational啊，先从一维去理解，给定长为n的数组A
从中任取区间[L,R]，计算\(\sum_{i=L}^{R}A_{i}*(i - L + 1)\)。
比如数组[1,2,3,4,5,6]，区间[L,R]=[3,5]，截取的子数组为[3,4,5]
然后计算S=3 * 1 + 4 * 2 + 5 * 3 = 26。
当有q次查询时，我们如何快速的计算呢？
这是一个很好的公式推导教学
\(S=\sum_{i=L}^{R}A_{i}*(i - L + 1)\) ->
\(S=\sum_{i=L}^{R}A_{i}*i - A_{i}* (L - 1)\)
左侧是\(A_{i}*i\) 右侧是\(A_{i}\)乘一个常数。
计算区间和常用策略是前缀和\(O(1)\)计算
很自然地，我们设sumA表示数组前i项之和，设sumAi表示数组前i项与i的乘积和，则有
\(S=sumAi_R-sumAi_{L-1} - (sumA_R - sumA_{L-1})*(L-1)\)
对于[3,4,5]的案例，等价的，\(S=3*3+4*4+5*5-(3+4+5)*2 = 26\)
下面我们回到原题的二维情况
\(S=\sum_{i=1}^{c}A_i*i\) 我们需要把i与子区域的索引转换关系
\(S=\sum_{i=x1}^{x2}\sum_{j=y1}^{y2}M_{ij}*((i-x1)*(y2-y1+1)+j-y1+1)\) 前面的二维求和 我们简写为\(\sum\)
\(S=\sum M_{ij}*i*(y2-y1+1) - \sum M_{ij}*(x1*(y2-y1+1)+y1-1) + \sum M_{ij}*j\)
到这里我们得到了一个二维求和的公式，观察到为了计算S，我们需要预处理三个二维前缀和。分别是
\(\sum M_{ij}*i\), \(\sum M_{ij}*j\) 和原始的\(\sum M_{ij}\)
对于每个二维前缀和 我们分别计算子区域的和 然后按公式相加即可。
下面贴完整代码
#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
#define vi vector<i64>
#define vvi vector<vi>
void solve()
{
int n, q; cin >> n >> q;
vvi nums(n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
i64 v; cin >> v;
nums[i].push_back(v);
}
}
vvi sum(n + 1, vi(n + 1)), sum_i(n + 1, vi(n + 1)), sum_j(n + 1, vi(n + 1));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
sum[i][j] += sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + nums[i - 1][j - 1];
sum_i[i][j] += sum_i[i - 1][j] + sum_i[i][j - 1] - sum_i[i - 1][j - 1] + nums[i - 1][j - 1] * i;
sum_j[i][j] += sum_j[i - 1][j] + sum_j[i][j - 1] - sum_j[i - 1][j - 1] + nums[i - 1][j - 1] * j;
}
}
auto sumRegion = [&](vvi& sum, int x1, int x2, int y1, int y2) -> i64 {
return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
};
vi ans;
while (q-- > 0) {
int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
i64 s1 = sumRegion(sum_i, x1, x2, y1, y2) * (y2 - y1 + 1);
i64 s2 = sumRegion(sum, x1, x2, y1, y2) * (x1 * (y2 - y1 + 1) + y1 - 1);
i64 s3 = sumRegion(sum_j, x1, x2, y1, y2);
ans.push_back(s1 - s2 + s3);
}
for (auto v : ans) cout << v << " ";
cout << endl;
}
int main() {
std::ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
cin >> t;
while (t-- > 0) {
solve();
}
}
