【构造】Ural Championship April 30, 2017 Problem K. King’s island
题意:让你构造一个n个点的简单多边形,使得所有点是整点,并且所有边长是整数,并且没有边平行于坐标轴。
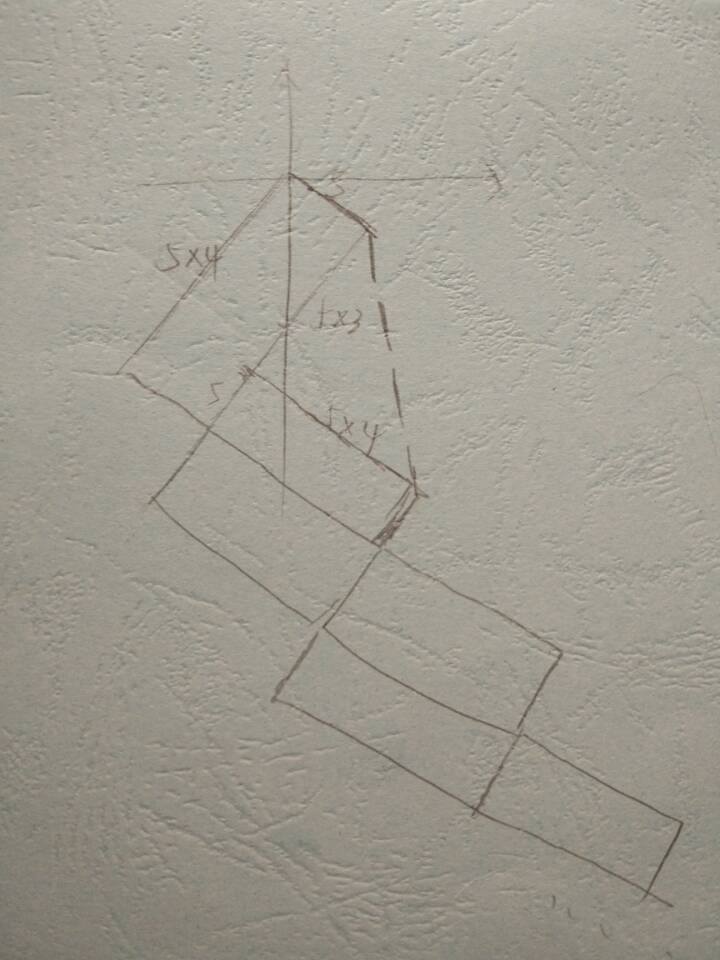
就利用勾股数,如下图这样构造即可,n为偶数时,只需矩形拼成,n为奇数时,封上虚线边即可。
#include<cstdio>
using namespace std;
struct Point{
int x,y;
Point(const int &x,const int &y){
this->x=x;
this->y=y;
}
Point(){}
}p[1005];
int n,e;
int main(){
// freopen("k.in","r",stdin);
bool tag=0;
int x=-8,y=-19;
scanf("%d",&n);
if(n==3){
puts("0 0\n4 3\n-20 21");
return 0;
}
if(n%2==1){
++n;
tag=1;
}
p[++e]=Point(0,0);
p[++e]=Point(-12,-16);
p[++e]=Point(-8,-19);
p[++e]=Point(4,-3);
for(int i=1;i<=(n-4)/2;++i){
if(i%2==1){
Point a[3];
a[0]=Point(x+4*4,y-4*3);
a[1]=Point(a[0].x+3,a[0].y+4);
a[2]=Point(x+3,y+4);
for(int j=e;j>=e/2+2;--j){
p[j+2]=p[j];
}
p[e/2+1]=a[0];
p[e/2+2]=a[1];
p[e/2+3]=a[2];
x=a[0].x;
y=a[0].y;
e+=2;
}
else{
Point a[3];
a[2]=Point(x-3,y-4);
a[1]=Point(a[2].x-4*4,a[2].y+4*3);
a[0]=Point(a[1].x+3,a[1].y+4);
for(int j=e;j>=e/2+1;--j){
p[j+2]=p[j];
}
p[e/2]=a[0];
p[e/2+1]=a[1];
p[e/2+2]=a[2];
x=a[2].x;
y=a[2].y;
e+=2;
}
}
if(tag){
p[e-1]=p[e];
--e;
}
for(int i=1;i<=e;++i){
printf("%d %d\n",p[i].x,p[i].y);
}
return 0;
}
——The Solution By AutSky_JadeK From UESTC
转载请注明出处:http://www.cnblogs.com/autsky-jadek/




