【推导】【NTT】hdu6061 RXD and functions(NTT)
题意:给定一个n次多项式f(x)的各项系数,让你求f(x-Σai)的各项系数。
http://blog.csdn.net/v5zsq/article/details/76780053
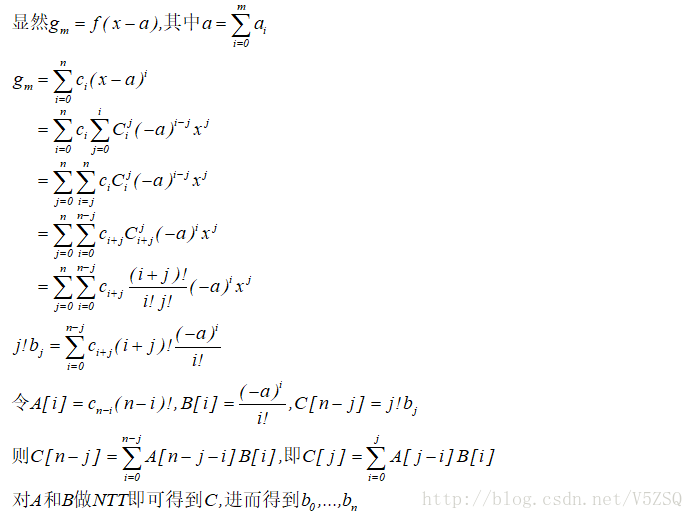
推导才是最关键的部分……我的数学推导能力很弱,比赛的时候很难推出来……尤其是累加变量交换顺序、换元这两个常用的技巧在配凑卷积形式以及莫比乌斯反演中都很常用
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
#define N ((1<<18)+5)
#define MOD 998244353ll
ll Quick_Pow(ll a,ll p){
if(p==0){
return 1ll;
}
ll res=Quick_Pow(a,p>>1);
res=res*res%MOD;
if((p&1ll)==1ll){
res=(a%MOD*res)%MOD;
}
return res;
}
struct NTT{
int n,rev[N];
ll g;
void ini(int lim) {
g=3;//1004535809,998244353的原根都是3
n=1;
int k=0;
while(n<lim){
n<<=1;
++k;
}
for(int i=0;i<n;++i){
rev[i]=((rev[i>>1]>>1)|((i&1)<<(k-1)));
}
}
void dft(ll a[],int DFT) {
for(int i=0;i<n;++i){
if(i<rev[i]){
swap(a[i],a[rev[i]]);
}
}
for(int l=2;l<=n;l<<=1){
int m=l>>1;
ll wn=Quick_Pow(g,DFT==1 ? (MOD-1ll)/(ll)l : MOD-1ll-(MOD-1ll)/(ll)l);
for(int i=0;i<n;i+=l){
ll w=1;
for(int k=0;k<m;++k){
ll t=w*a[i+k+m]%MOD;
a[i+k+m]=(a[i+k]-t+MOD)%MOD;
a[i+k]=(a[i+k]+t)%MOD;
w=w*wn%MOD;
}
}
}
if(DFT==-1){
ll inv=Quick_Pow(n,MOD-2ll);
for(int i=0;i<n;++i){
a[i]=a[i]*inv%MOD;
}
}
}
void mul(ll a[],ll b[],int len) {
ini(len);
dft(a,1);
dft(b,1);
for(int i=0;i<n;++i){
a[i]=a[i]*b[i];
}
dft(a,-1);
}
}ntt;
ll c[N],A[N],B[N],jc[N],jcni[N];
int n,m;
int main(){
jc[0]=1;
jcni[0]=1;
for(int i=1;i<=100000;++i){
jc[i]=(jc[i-1]*(ll)i)%MOD;
jcni[i]=Quick_Pow(jc[i],MOD-2ll);
}
ll x;
// freopen("hdu6061.in","r",stdin);
while(scanf("%d",&n)!=EOF){
memset(A,0,sizeof(A));
memset(B,0,sizeof(B));
for(int i=0;i<=n;++i){
scanf("%lld",&c[i]);
}
ll a=0;
scanf("%d",&m);
for(int i=1;i<=m;++i){
scanf("%lld",&x);
a=(a+x)%MOD;
}
ll pw=1;
for(int i=0;i<=n;++i){
A[i]=(c[n-i]*jc[n-i])%MOD;
B[i]=(pw*jcni[i])%MOD;
pw=(pw*(MOD-a))%MOD;
}
ntt.mul(A,B,n*2+1);
for(int i=0;i<=n;++i){
printf("%lld ",(A[n-i]*jcni[i])%MOD);
}
puts("");
}
return 0;
}
——The Solution By AutSky_JadeK From UESTC
转载请注明出处:http://www.cnblogs.com/autsky-jadek/



